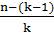31. Отношение порядка. Свойства отношений.

Отношением р на множестве М называется отношением строгого порядка:

1.Иррефлексивность

2.Асиметричность

3.Транзитивность

Отношения могут обладать рядом свойств, которые определяются через условия, которым должны удовлетворять их элементы

Пусть р на множестве А, тогда р называется:

1. иррефлексивным, если

2) транзитивным, если

3)ассимметричным, если

Отношением р на множестве М называется отношением нестрогого порядка:

1.Рефлексивность

2.Антисимметричность

3.Транзитивность

Пусть р на множестве А, тогда р называется:

1) рефлексивным, если

2)антисимметричным, если

3)транзитивным, если

32. Отображения и их основные свойства. Виды отображений.

Мн-во F(x) первых компонент мн-ва F (мн-во всех прообразов) называется областью определения отображения N.

Мн-во F(y) вторых компонент мн-ва F (мн-во всех образов) называется областью значений отображения N.

Виды:

1. F(x)=x – всюду определённое;

2. F(y)=y – называется отображением х на у.

3. Если каждый элемент х из мн-ва х имеет не более 1 образа в у, то отображение N называется функциональным (однозначным) отображением или функцией.

4. Отображение N в минус первой степени является обратным отображению N.

5. Отображение N называется взаимно однозначным, если N является всюду определённым функциональным отображением х на у, а N в минус первой степени – всюду определённым отображением у на х.

33. Комбинаторные структуры (размещение, перестановки, сочетания)

Комбинаторика – раздел математики, в котором изучаются методы подсчета числа комбинаций определенного вида, составленных из элементов конечного множества.

Перестановкой из n элементов называется любой упорядоченный набор этих элементов, т.е. место элемента в наборе, порядок перечисления имеют значение.

P_n = n × (n - 1) ×...× 1 = n!

Размещением, содержащим k элементов из n имеющихся называется любой упорядоченный набор, содержащий k элементов, выбранных из n имеющихся.

Сочетанием, содержащим k элементов, выбранных из n имеющихся, называется любой неупорядоченный набор, содержащий k элементов, выбранных из n имеющихся.

В неупорядоченном наборе порядок перечисления элементов не важен.

=

34. Перестановка с учетом повторения.

Перестановка с повторением означает, что если существует последовательность с одинаковыми элементами, при их перестановке последовательность не изменится.

= , где n = n₁ + n₂ +…+ n_k

35. Сочетания с учётом повторений.

Сочетанием с повторением из n элементов по k элементам называется всякая последовательность из k элементов:

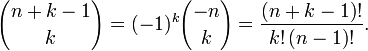
36. «Бином Ньютона»

(a +b)ⁿ = aⁿ + C_n¹a^n-1b + C_n²a^n-2b^n-2 + C_n³a^n-3b³ + … + bⁿ .

Компоненты формулы «Бином Ньютона»

• Первая часть формулы – разложение бинома

• - ,биномиальные коэффициенты

• Общий член разложения бинома n-й степени.

Где T – член разложения.

(K+1)- порядковый номер разложения.

37. Биноминальные коэффициенты. Свойства биномиальных коэффициентов.

Биномиальные коэффициенты

Биномиальным коэффициентом   называется количество способов выбрать набор   предметов из  различных предметов без учёта порядка расположения этих элементов (т.е. количество неупорядоченных наборов).

Также биномиальные коэффициенты - это коффициенты в разложении   (т.н. бином Ньютона):

Свойства:

1. 

2. Число всех членов разложения на единицу больше показателя степени бинома то есть равно (n+1)

3. Сумма показателей степеней а и b каждого члена разложения равна показателю степени бинома то есть n

4. Биномиальные коэффициенты членов разложения равноотстоящих от концов разложения, равны между собой 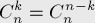«правило симметрии»

5. Сумма биномиальных коэффициентов всех членов разложения равна 2”

6. Сумма биномиальных коэффициентов, стоящих на нечетных места равна сумме биномиальных коэффициентов, стоящих на четных местах и равна .

7. Правило Паскаля

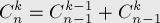
8. Любой биномиальный коэффициент начиная со второго, равен произведению предшествующего биномиального коэффициентам дроби

9.