1.4 Определение коэффициента корреляции (корреляционного отношения) и средней относительной ошибки аппроксимации
Теснота
связи между двумя параметрами
характеризуется коэффициентом корреляции
(
)
для линейных зависимостей и корреляционным
отношением (
)
для нелинейных; дополнительной оценкой
точности аппроксимации является средняя
относительная ошибка аппроксимации
(
).
Данные параметры определяем для рассмотренных видов регрессии:
а) парной линейной
%
б) парной логарифмической
%
в) парной степенной
%
Полученные результаты сравниваем между собой, используя таблицу 5.
Таблица 5 – Сравнение полученных уравнений регрессии
Уравнение регрессии |
( ) |
, % |
Вывод |
|
0,9988 |
1,794 |
Да |
|
0,981 |
4,869 |
Нет |
|
0,9998 |
1,869 |
Нет |
По данным таблицы 5 можно сделать вывод о том, что наилучшей аппроксимацией (по ( ) и ) для рассматриваемого примера обладает парная линейная регрессия. Поэтому именно для нее будем вести дальнейший анализ.
1.5 Построение графиков линий парной регрессии
По полученным выше уравнениям парной регрессии строим графики зависимости трудоемкости монтажа блоков от их массы (рисунок 3):
а) для линейной регрессии
при
:
при
:
б) для логарифмической регрессии
Построение выполняем по исходным данным ( ) и расчетным значениям ( ), приведенным в таблице 3.
в) для степенной регрессии
Построение выполняем по исходным данным ( ) и расчетным значениям ( ), приведенным в таблице 4.
Рисунок 3 – Графики линейной парной регрессии
1.6 Проверка достаточности (репрезентативности выборки)
Оцениваем
репрезентативность выборки (таблица
6), то есть определяем, можно ли по ней
судить о генеральной совокупности. Для
этого количество наблюдений должно
быть не менее достаточного, то есть:
.
Достаточное число наблюдений определяем
как
,
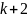где
– число степеней свободы, которое
зависит от аргумента функции распределения
вероятности (
)
и заданной доверительной вероятности
(
),
то есть
.
Доверительная вероятность обычно
задается равной 0,90; 0,95; 0,99. Аргумент
функции распределения вероятности
определяем из соотношения:
,
(4)
где
- оценка абсолютного отклонения.
Порядок
определения параметра
,
зависящего от других расчетных параметров,
приведен в таблице 6. Необходимый для
этого параметр
- среднее квадратическое отклонение –
рассчитываем как квадратный корень
дисперсии фактических значений
независимой и зависимой переменных
(
),
определяемой по формулам:
,
(5)
.
(6)
Если соотношение выполняется, то данное число наблюдений является достаточным и по нему можно судить о генеральной совокупности.
Таблица 6 – Проверка достаточности выборки
Наименование параметров |
Расчетная формула, обозначение |
Значение параметра для |
|||
|
|
||||
ед. изм. |
значение |
ед. изм. |
значение |
||
1 Число наблюдений в выборке |
N |
шт. |
16 |
шт. |
16 |
2
Средние арифметические значения
переменных ( |
|
кг |
13,5 |
чел.-ч |
19,752 |
3
Дисперсия ( |
;
|
- |
22,67 |
- |
59,393 |
4
Среднее квадратическое отклонение
( |
|
кг |
4,76 |
чел.-ч |
7,707 |
5
Степень точности средних квадратических
отклонений среднего ( |
|
кг |
1,23 |
чел.-ч |
1,990 |
6 Расчетное число степеней свободы |
|
- |
15 |
- |
15 |
7 Табличное значение критерия Стъюдента |
|
- |
2,947 |
- |
2,947 |
8
Оценка абсолютного отклонения ( |
|
кг |
3,62 |
чел.-ч |
5,864 |
9 Аргумент функции распределения вероятности |
|
- |
0,761 |
- |
0,761 |
10 Табличное число степеней свободы |
|
- |
|
- |
|
11 Достаточный объем выборки |
|
шт. |
|
шт. |
|
12 Вывод о достаточности выборки |
|
шт. |
|
шт. |
|
|
|||||
;
)
;
;
)
;
)
;
;
)
;
;
)
;
;
