Московский Авиационный Институт

(Государственный Технический Университет)

Расчетно-графическая работа по дисциплине

«Динамика и прочность»

Преподаватель Снеткова Е. И.

Студент гр. 02-401 Кожухова О. А.

Москва

2012

Оглавление

Введение………………………………………………………………………. 3

1. Расчет частоты колебаний лопатки………………………………………..	4
Исходные данные……………………………………………………….	4
Задание №1 …………………………………………………………….	5
Задание №2……………………………………………………………..	8
2. Расчёт на прочность диска компрессора………………………………….	11
Исходные данные……………………………………………………….	11
2.1 Расчёт на прочность диска компрессора без центрального отверстия……………………………………………………………………….	12
2.2 Расчёт на прочность диска компрессора с центральным отверстием……………………………………………………………………..	15
2.2.1 Вариант расчёта диска с маленьким отверстием……….	15
2.2.2 Вариант расчёта диска с большим отверстием………….	16
2.2.3 Вариант расчёта диска с большим отверстием…………..	17
2.3 Расчёт на прочность диска компрессора со ступицей………….	19
3. Расчет критических частот вращения ротора……………………………	22

Список используемой литературы…………………………………………… 24

Введение.

В данной работе мы рассчитали первые три частоты собственных колебаний лопатки. Так же, рассчитываем диск на прочность, изучаем зависимость радиальных и окружных напряжений от наличия и размера отверстия и ширины ступицы. Так же изучаем зависимость критических частот вращения ротора от жёсткости подшипников.

1. Расчёт частоты колебания лопатки Исходные данные

L- длина лопатки.

R_k – радиус расположения корневого сечения.

ω – Угловая скорость вращения рабочего колеса.

ρ – плотность материала лопатки.

N_c – число поперечных сечений с заданной геометрической характеристикой.

F(i), где i = 1… N_c – массив площадей поперечных сечений.

J(i) – массив минимальных моментов инерции поперечных сечений (сечения в которых задаются геометрические характеристики делят лопатку на равные по длине участки; изменение характеристик в приделах каждого участка происходит по линейному закону)

N_m – число сосредоточенных масс дискретной модели упруго-инерционной системы лопатки, создаваемой на основании введённых данных (крыло лопатки с заданной геометрией делится на N_m элементов равной длины; для каждого элемента рассчитывается масса; масса каждого элемента представляется дискретной точечной массой в сечении, расположенном посреди элемента; участки, расположенные между корневым сечением и сечениями с дискретными массами полагаются безынерционными стержнями постоянного поперечного сечения, геометрические характеристики которых определяются, как среднее значение характеристик граничных сечений при расчёте деформации стержневых элементов дискретной модели принимается во внимание только изгибная деформация).

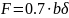, [м²] (1.1)

, [м⁴] (1.2)

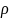= 4500, [кг·м³]

E_m = 0.11·10⁵, [МПа]

Требуется:

1. Рассчитать первые три собственные частоты для двух вариантов, в которых N_c принимает значения 2 и 3. В обоих вариантах ω = 0, N_m = 5.

2. Произвести расчёт первых трёх собственных частот колебания лопатки при вращении колеса с 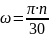, N_c = 2; 3, N_m = 5.

Задание №1

Геометрические характеристики i-ого сечения лопатки; N_c = 3 приведены в таблице 1.1.

Таблица 1.1

i	1	2	3
Zi	0	0.0275	0.055
Fi	3.617·10-5	1.689·10-5	7.801·10-6
Ji	8.454·10-10	2.468·10-10	7.821·10-11

Дискретная модель: Nm=5; M= 4.836·10^-3, таблица 1.2.

Таблица 1.2

i	1	2	3	4	5	6
M(i)/M	0.3308	0.2518	0.1833	0.1357	0.0985	0
L(i)/DL	0.1	0.3	0.5	0.7	0.9	1

Форма колебаний для ω = 0 рад/с приведена в таблице 1.3.

Таблица 1.3

Частота f, Гц	Форма колебаний
	Y(1)	Y(2)	Y(3)	Y(4)	Y(5)	Y(6)
64.1	0.0357	0.1768	0.3628	0.5927	0.8622	1
276.7	-0.0641	-0.2793	-0.3800	-0.1454	0.5908	1
710.8	0.1269	0.4116	0.0214	-0.6376	0.3537	1

На Рисунке 1.1 показана форма колебаний лопатки для N_c = 3, при ω = 0 рад/с и частотах f1 = 64.1 Гц, f2 = 276.7 Гц, f3 = 710.8Гц.

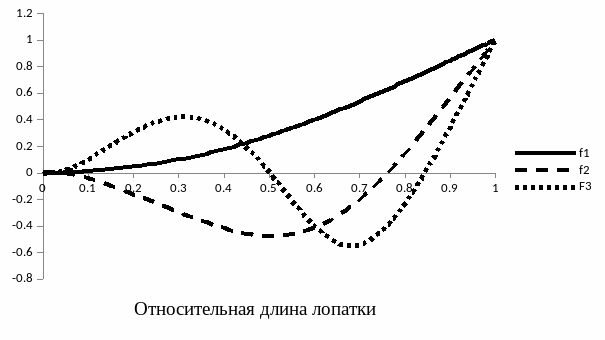
Рисунок 1.1 - Форма колебаний лопатки.

Геометрические характеристики i-ого сечения лопатки; N_c = 2 приведены в таблице 1.4

Таблица 1.4

i	1	2
Zi	0	0.055
Fi	3.617·10-5	7.801·10-6
Ji	8.454·10-10	7.821·10-11

Дискретная модель: Nm=5; M= 5.441·10^-3, таблица 1.5

Таблица 1.5

i	1	2	3	4	5	6
M(i)/M	0.3032	0.2516	0.2000	0.1484	0.0968	0
L(i)/DL	0.1	0.3	0.5	0.7	0.9	1

Форма колебаний для ω = 0 рад/с приведена в таблице 1.6

Таблица 1.6

Частота f, Гц	Форма колебаний
	Y(1)	Y(2)	Y(3)	Y(4)	Y(5)	Y(6)
65.52	0.0136	0.119	0.3114	0.5655	0.853	1
307.7	-0.0497	-0.3108	-0.4406	-0.1374	0.5873	1
787.2	0.1089	0.411	-0.0339	-0.4877	0.367	1

На Рисунке 1.2 показана форма колебаний лопатки для N_c = 2, при ω = 0 рад/с и частотах f1 = 65.52 Гц, f2 = 307.7 Гц, f3 = 787.2 Гц.

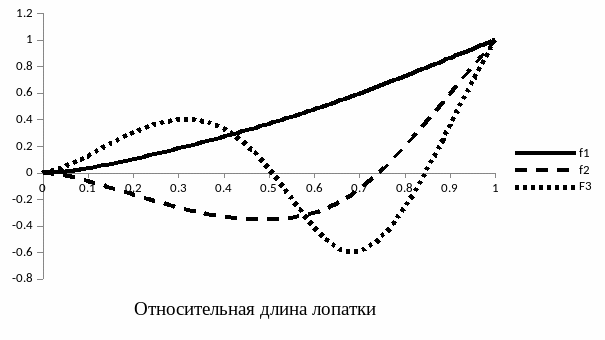
Рисунок 1.2 - Форма колебаний лопатки

Собственные частоты лопатки fi, Гц, при N_c = 2 и N_c = 3 приведены в таблице 1.7:

Таблица 1.7

i	Nc = 2	Nc = 3
1	65.52	64.1
2	307.7	276.7
3	787.2	710.8