1.4. Метод замены переменной (метод подстановки)
Теорема.
Пусть функция
определена и дифференцируема на некотором
промежутке
,
– множество значений этой функции. Если
на множестве
функция
имеет первообразную, то для множества
справедлива формула:
,
которая называется
формулой
замены переменной в неопределенном
интеграле.
Замечание. При замене переменной в неопределенном интеграле иногда более удобно задавать не х как функцию t, а наоборот, t как функцию от х.
Пример
1.
Найти
.
Решение
=
.
Пример
2.
Найти
.
Решение.
.
Замечание.
Аналогично
вычисляется интеграл
:
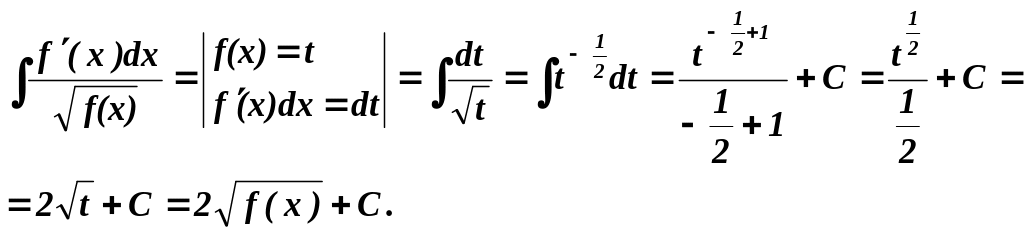
Пример
3.
Найти
.
Решение.
=
.
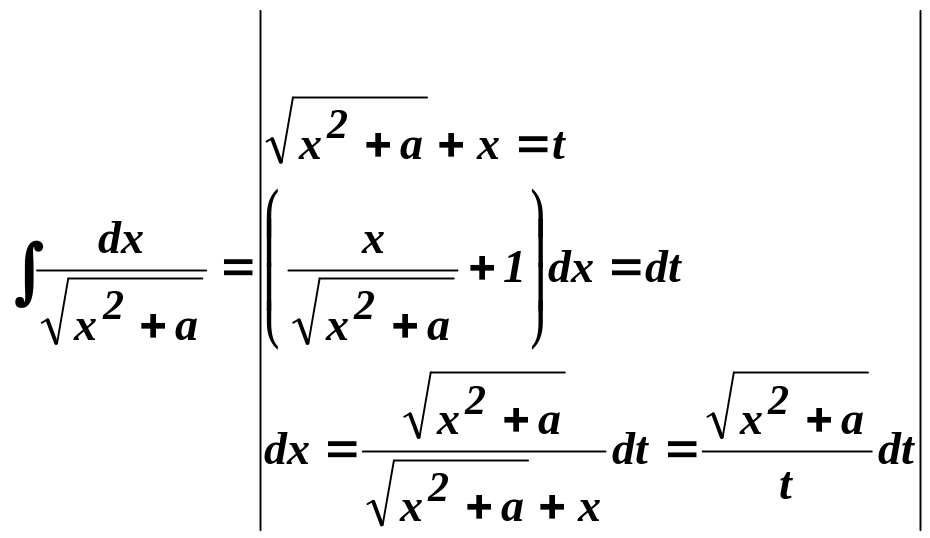Пример
4.
Найти
.
Решение
=
.
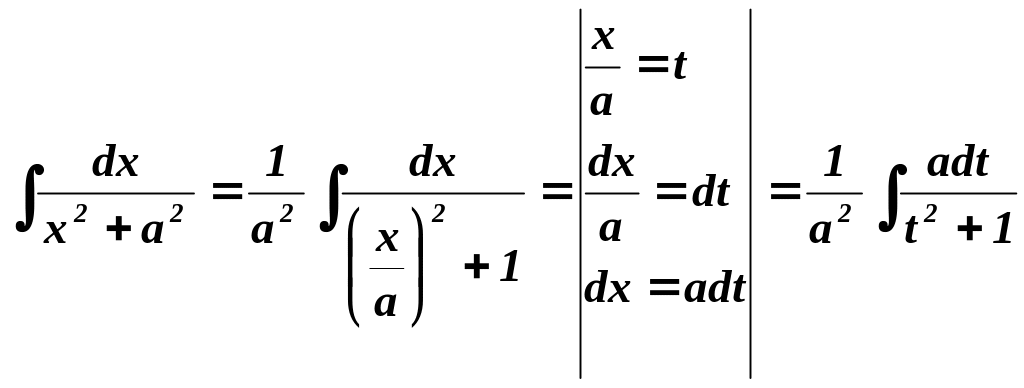Пример
5. Найти
.
Решение
.
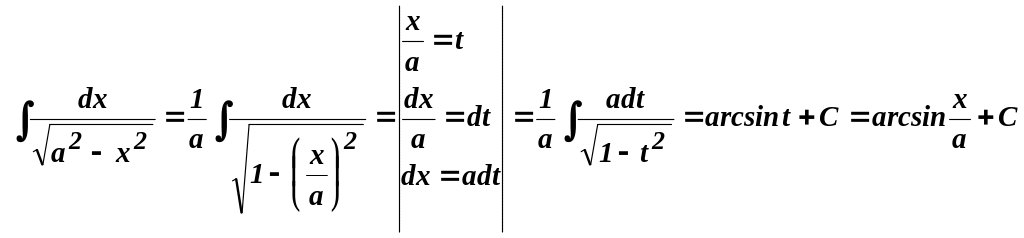Пример
6. Найти
.
Решение
.
Замечание.
При
помощи той же
формулы
замены
вычисляются интегралы
,
,
и т.д.
Пример
7. Найти
.
Решение
.
Замечания.
1.
Аналогично
вычисляется интеграл
заменой
.
.
2. Таблицу можно дополнить интегралами из примеров 2–7, а также следующими:
15.
|
16.
|
17.
|
18.
|
19.
= |
|
20.
= |
21.
|
22.
|
23.
= |
24.
|
|
25.
|
26.
|
27.
|
28. . |
;
;
;
;
;
;
;
;
;
;
;
;
;
1.5. Интегрирование по частям
Теорема.
Пусть u(x)
и v(x)
определены и дифференцируемы на некотором
промежутке x
и пусть функция
имеет первообразную на этом промежутке.
Тогда на
функция
также имеет первообразную и справедлива
формула:
(1.2)
Формула (1.2) называется формулой интегрирования по частям в неопределенном интеграле.
Так
как
и
,
то ее можно записать в виде
.
(1.3)
Замечание.
Эта формула позволяет свести вычисление
к вычислению интеграла
,
который может оказаться более простым.
Пример
1.
Найти
.
Решение.
=
Пример
2.
Найти
.
Решение.
=
.
1.6. Интегрирование выражений, содержащих квадратный трехчлен
Для вычисления интегралов вида:
1.
;
2.
;
3.
;
4.
;
5.
,
содержащих квадратный трехчлен, применяют
следующие преобразования:
1) выделяем полный квадрат из квадратного трехчлена, то есть
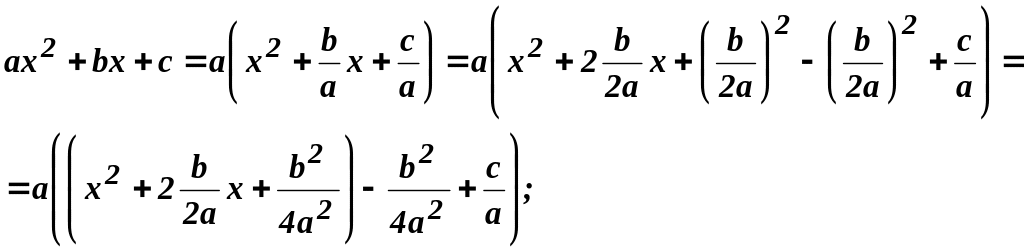
2) полный квадрат преобразуем в квадрат двучлена:
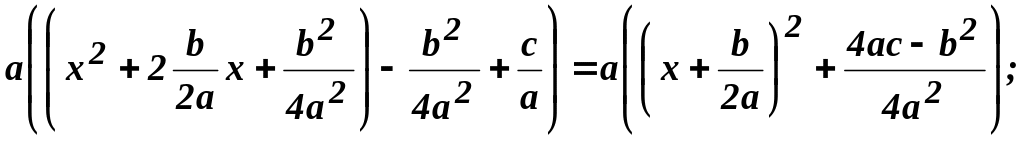
3)
делаем замену
,
в результате чего интегралы после
преобразований приводятся к табличным.
Пример
1.
Найти
.
Решение.
Пример
2.
Найти
.
Решение.
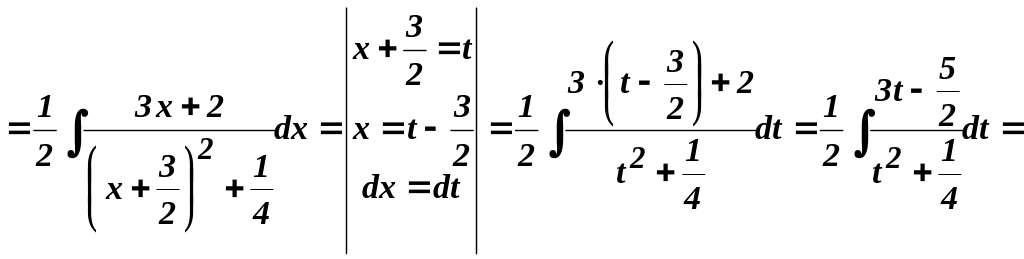
Пример
3.
Найти
.
Решение.
=
.
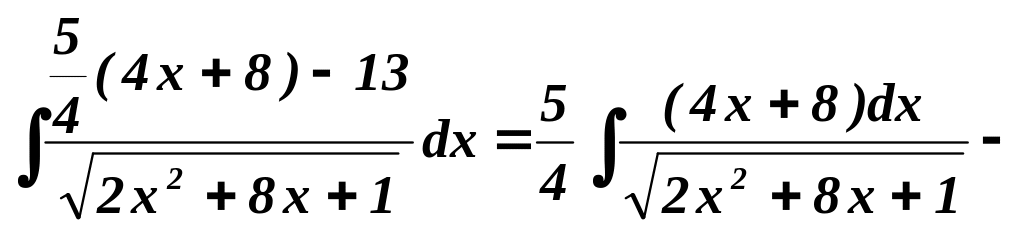
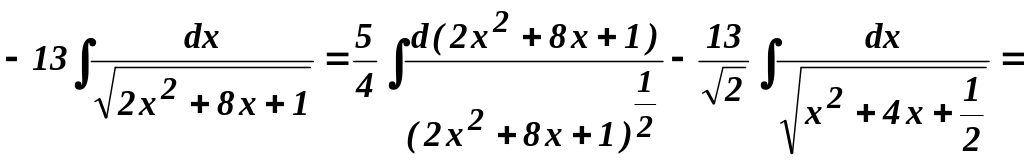
1.7. Интегрирование рациональных функций
Определение.
Рациональной
функцией
называется функция, равная отношению
двух многочленов:
где
,
– целые положительные числа;
Если < , то называется правильной дробью, в противном случае – неправильной.
Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби.
Пример.
Представить
неправильную дробь
в виде суммы многочлена и правильной
дроби.
Решение. Делим по правилу деления многочленов:
Таким
образом,
.
Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к освоению интегрирования правильных дробей. Поэтому в дальнейшем будем рассматривать функции при условии < .
Определение. Простейшей дробью называется дробь одного из следующих четырех типов:
,
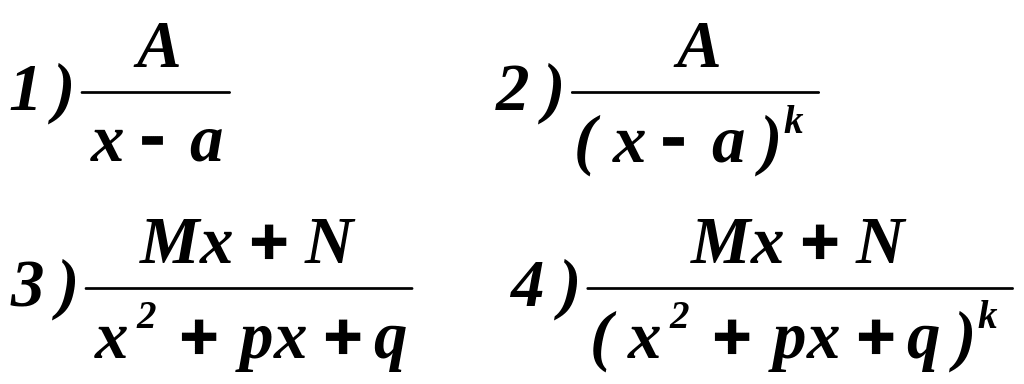где
,
,
,
,
,
– постоянные
числа;
– натуральное число,
,
– неразложимый квадратный трехчлен, у
которого отрицательный дискриминант,
т. е.
Рассмотрим интегралы от простейших дробей:
.
.
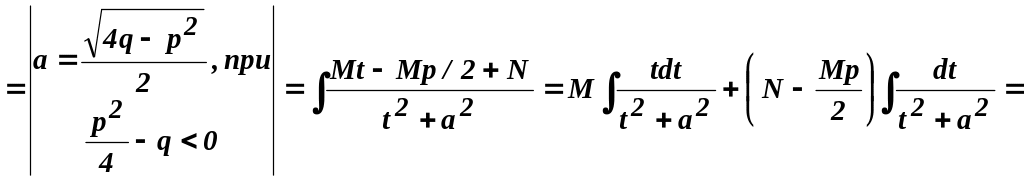
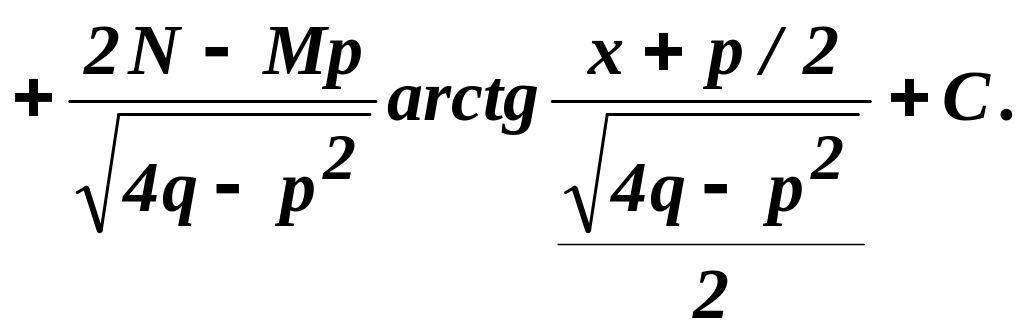
Выделим в числителе производную от квадратного трехчлена, стоящего в знаменателе:
Первый
интеграл в правой части равенства легко
находится с помощью подстановки
,
а второй преобразуем следующим образом:
Последний
интеграл в случае
является табличным, а в остальных случаях
берется с помощью рекуррентной формулы.
Таким образом, всякая рациональная дробь может быть проинтегрирована в элементарных функциях.
Пример
1.
Найти
.
Решение.
=
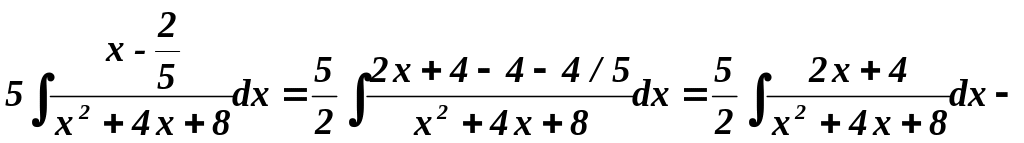
Пример
2.
Найти
.
Решение.
=
=
