Задание №1
1. Роль моделирования в познании, виды моделей, информационное наполнение моделей, математические модели как важный инструмент исследования экономики.
2. По данным, приведённым в таблице, рассчитать среднюю арифметическую, как прогнозную оценку ряда:
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Значение Yt |
13 |
12 |
12 |
14 |
11 |
9 |
11 |
12 |
15 |
11 |
8 |
9 |
10 |
12 |
11 |
10 |
13 |
12 |
9 |
14 |
Вычислить ошибку отклонения:
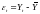
и дисперсию:
.
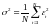Определить доверительные границы прогноза, выполняемого с помощью средней арифметической, используя правило трёх сигм:
.
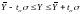Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №4
1. Классификация методов прогнозирования.
2. Применить к данным таблицы модель Брауна:
- при α=0,2.
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Yt |
80 |
60 |
48 |
42 |
36 |
24 |
21 |
28 |
42 |
39 |
36 |
30 |
50 |
150 |
60 |
80 |
60 |
55 |
45 |
38 |
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №2
1. Классификация ЭММ, ЭММ в логистике, математические методы и экономико-математические модели.
2. Применить к данным таблицы модель Брауна:
- при α=0,1.
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Yt |
80 |
60 |
48 |
42 |
36 |
24 |
21 |
28 |
42 |
39 |
36 |
30 |
50 |
150 |
60 |
80 |
60 |
55 |
45 |
38 |
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №3
1. Основные понятия прогностики.
2. По данным таблицы вычислить коэффициент парной корреляции:
Табл. 2
Ставка рефинансирования ЦБ РФ с 19 августа 1996 по 1 января 2012 г.
Годы |
Конечное потребление, G |
Валовое накопление, C |
106 млн. руб |
106 млн. руб |
|
1998 |
2,10 |
0,44 |
1999 |
3,30 |
0,729 |
2000 |
4,48 |
1,37 |
2001 |
5,89 |
1,96 |
2002 |
7,44 |
2,17 |
2003 |
9,02 |
2,76 |
2004 |
11,40 |
3,56 |
2005 |
14,32 |
4,34 |
2006 |
17,63 |
5,75 |
2007 |
21,79 |
8,03 |
2008 |
27,24 |
10,64 |
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №5
1. Виды прогнозов, классификация прогнозов по периоду прогнозирования.
2. По данным, приведённым в таблице, рассчитать среднюю арифметическую, как прогнозную оценку ряда:
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Значение Yt |
13 |
12 |
11 |
14 |
11 |
9 |
11 |
12 |
10 |
11 |
8 |
9 |
10 |
12 |
11 |
10 |
13 |
12 |
15 |
14 |
Вычислить ошибку отклонения:
и дисперсию:
.
Определить доверительные границы прогноза, выполняемого с помощью средней арифметической, используя правило трёх сигм:
.
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №6
1. Средняя арифметическая, средняя взвешенная и скользящая средняя в краткосрочном прогнозировании.
2. Применить к данным таблицы модель Брауна:
- при α=0,3.
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Yt |
80 |
60 |
48 |
42 |
36 |
24 |
21 |
28 |
42 |
39 |
36 |
30 |
50 |
150 |
60 |
80 |
60 |
55 |
45 |
38 |
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №7
1. Экспоненциальное сглаживание как вид скользящей взвешенной средней. Вывод формулы Брауна.
2. С помощью метода графического анализа определить вид зависимости между возрастной группой работников и средней начисленной заработной платой.
После чего с помощью метода наименьших квадратов (МНК) оценить значения коэффициентов этой модели.
Средняя начисленная заработная плата работников по возрастным группам в 2009 году
Все работники |
18084 |
в том числе по возрастным группам: от 18 до 19 лет |
10832 |
от 20 до 24 лет |
15693 |
от 25 до 29 лет |
19112 |
от 30 до 34 лет |
20122 |
от 35 до 39 лет |
19295 |
от 40 до 44 лет |
18394 |
от 45 до 49 лет |
18313 |
от 50 до 54 лет |
17698 |
от 55 до 59 лет |
17137 |
от 60 до 64 лет |
16665 |
65 лет и выше |
15687 |
Для случая линейной модели МНК приводит к необходимости решения системы нормальных уравнений:
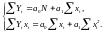
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №8
1. Анализ значений постоянной сглаживания, пределы изменения постоянной сглаживания.
2. С помощью метода графического анализа определить вид зависимости между возрастной группой работников и средней начисленной заработной платой.
После чего с помощью метода наименьших квадратов (МНК) оценить значения коэффициентов этой модели.
Для случая линейной модели МНК приводит к необходимости решения системы нормальных уравнений:
Среднемесячная номинальная начисленная заработная плата работников организаций по видам экономической деятельности
|
1995 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
Вся экономика |
472,4 |
2223,4 |
3240,4 |
4360,3 |
5498,5 |
6739,5 |
8554,9 |
10633,9 |
13593,4 |
17290,1 |
18637,5 |
Сельское хозяйство, охота и лесное хозяйство |
259,4 |
985,1 |
1434,6 |
1876,4 |
2339,8 |
3015,4 |
3646,2 |
4568,7 |
6143,8 |
8474,8 |
9619,2 |
Заведующий каф. ОиУ проф. А.Ю.Череповицын
Задание №9
1. Выбор оптимального значения постоянной сглаживания.