1. Матрицы. Определители. Системы линейных уравнений.

1. Матрицы: основные определения (матрица, размер матрицы, квадратные и прямоугольные матрицы, матрица-строка и матрица-столбец, равные матрицы, диагонали матрицы, ноль-матрица, единичная матрица). Сложение и вычитание матриц. Умножение матрицы на скаляр.

Пример. Найти матрицу 3А + 2В, если:

2. Матрицы: арифметические действия над матрицами (сложение и вычитание матриц, умножение матрицы на скаляр, умножение матриц). Транспонирование матриц.

Пример. Умножить матрицу А на матрицу В и наоборот, если:

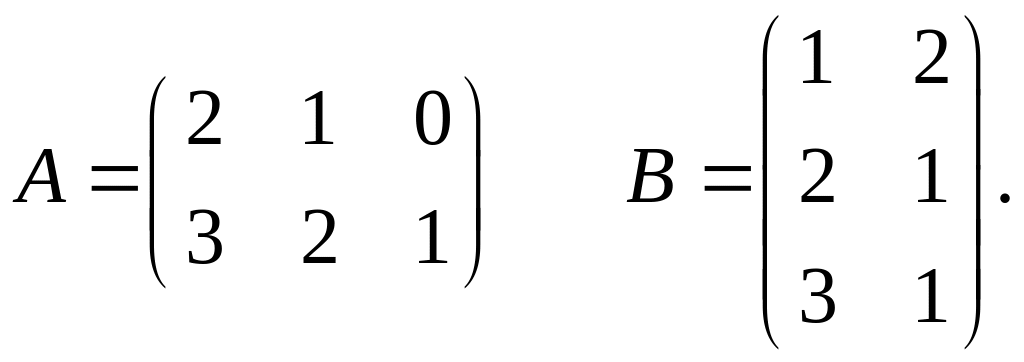
3. Определители: основные определения (определитель, главная диагональ, порядок, минор, алгебраическое дополнение). Основные свойства определителей.

Пример: Вычислить все алгебраические дополнения для определителя:

4. Методы раскрытия определителей второго и третьего порядка. Метод Саррюса для определителей третьего порядка. Метод понижения порядка.

Пример. Вычислить определитель А методом Саррюса и методом понижения порядка (по второй строке):

5. Системы линейных уравнений: основные определения: квадратная и прямоугольная СЛУ, определитель системы. Метод Крамера.

Пример. Решить СЛУ методом Крамера:

2. Векторы.

1. Векторы: основные определения: скалярная величина, векторная величина, вектор, коллинеарные и компланарные векторы, равенство векторов, орт вектора, угол между векторами и вектором и осью, проекция вектора на ось, координаты, направляющие углы и косинусы вектора, модуль вектора. Формулы, связывающие основные понятия для векторов.

Пример. Вычислить направляющие косинусы вектора ={12;-15;-16}.

2. Линейные операции над векторами. Необходимый и достаточный признак коллинеарности векторов.

Пример. Даны векторы: ={3;-2;6}; ={-2;1;0}; ={-3;0;9}. Найти вектор: =2 - + /3.

Решить эту же задачу графически, задав самостоятельно на плоскости векторы , , .

3. Скалярное произведение векторов и его свойства. Угол между двумя векторами. Физический смысл скалярного произведения.

Пример. При каком значении m вектор ={2;3;-1} перпендикулярен вектору ={1;-5;m}.

4. Тройка векторов. Правые и левые тройки векторов. Правила определения направленности тройки. Векторное произведение векторов и его свойства. Геометрический смысл векторного произведения.

Пример. Найти вектор x и его модуль, если вектор ={2;3;-1}, а вектор ={3;-1;-4}.

5. Смешанное произведение векторов и его свойства. Геометрический смысл смешанного произведения. Условие компланарности трех векторов.

Пример. Вычислить объем пирамиды с вершинами в точках: О(0;0;0); А(5;2;0); В(2;5;0); С(1;2;4).

3. Аналитическая геометрия.

1. Прямая на плоскости. Виды уравнений прямой на плоскости:

а) через заданную точку с нормальным вектором;

б) общее уравнение прямой;

в) каноническое уравнение прямой;

г) уравнение прямой через две точки;

г) параметрические уравнения прямой.

Пример. Написать общее уравнение прямой, проходящей через точки: А(1;2) и В(-2;3).

2. Прямая на плоскости. Виды уравнений прямой:

а) каноническое уравнение прямой;

б) уравнение прямой через две точки;

в) уравнение прямой в отрезках;

г) уравнение прямой через заданную точку в заданном направлении;

д) уравнение прямой с угловым коэффициентом.

Пример. Задана прямая: 2y – 2x + 3 = 0. Записать уравнение этой прямой в отрезках.

3. Прямая на плоскости. Расстояние от точки до прямой. Точка пересечения прямых. Угол между прямыми. Необходимые и достаточные признаки параллельности и перпендикулярности прямых на плоскости.

Пример. Найти расстояние от точки В(0;3) до прямой: 5x-12y-23=0.

4. Плоскость в пространстве. Виды уравнений плоскости:

а) уравнение плоскости через точку с нормальным вектором;

б) общее уравнение плоскости и неполные уравнения плоскости;

в) уравнение плоскости в отрезках;

г) уравнение прямой через три точки.

Пример. Написать общее уравнение плоскости, проходящей через три точки: А(1;-1;0); В(2;1;-3) и С(-1;0;1).

5. Плоскость в пространстве. Расстояние от точки до плоскости. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Точка пересечения трех плоскостей.

Пример. Найти расстояние от точки А(1;0;-2) до плоскости: 2x - y + 2z - 4 = 0.

6. Прямая в пространстве. Виды уравнений прямой:

а) общие уравнения прямой;

б) каноническое уравнение прямой;

г) уравнение прямой через две точки;

в) параметрические уравнения прямой.

Пример. Привести общие уравнения прямой к каноническому виду:

7. Прямая в пространстве: Угол между двумя прямыми. Необходимые и достаточные условия параллельности и перпендикулярности прямых в пространстве. Взаимное расположение прямой и плоскости в пространстве: угол между прямой и плоскостью. Необходимые и достаточные условия параллельности и перпендикулярности прямой и плоскости. Точка пересечения прямой и плоскости.

Пример. Найти уравнение плоскости, проходящей через прямую:

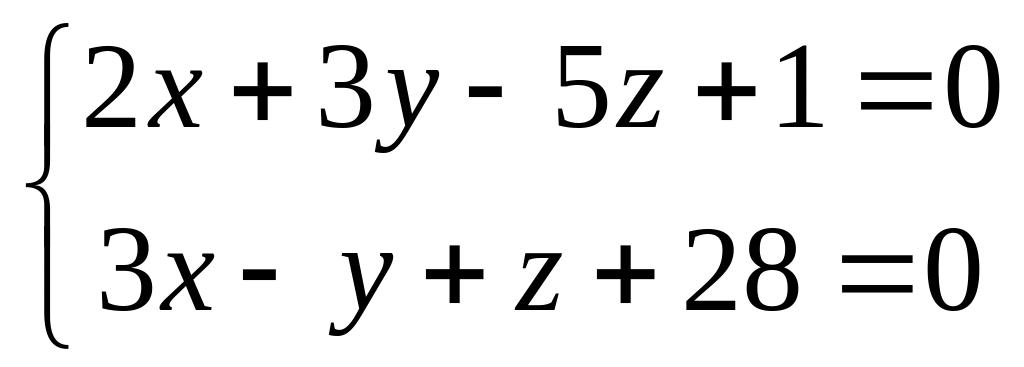
и точку М(1;-2;3).

8. Кривые второго порядка: окружность, эллипс, гипербола, парабола (основные характеристики, уравнения, графики).

Пример. Определить какая кривая описывается уравнением и построить ее: 9 х² + 25 y² = 225.