Лабораторная работа №5 Математический анализ: интегральное исчисление функции одной и многих переменных. Преобразование Лапласа.
Контрольные задания
Вычислить неопределенный интеграл
.
> restart;
> Int((x^3-6)/(x^4+6*x^2+8),x)=
int((x^3-6)/(x^4+6*x^2+8),x);
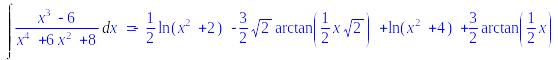
Ответ:
Вычислить несобственный интеграл
при a>0
b>0
для случаев a>b,
a=b,
a<b.
> restart;
> assume(a>0):assume(b>0):
> additionally(a>b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity);
Ответ:
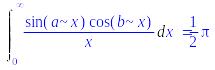
> restart;
> assume(a>0):assume(b>0):
> f:=sin(a*x)*cos(b*x)/x:
> additionally(a=b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity);
Ответ: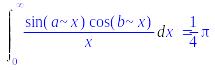
> restart;
> assume(a>0):assume(b>0):
> f:=sin(a*x)*cos(b*x)/x:
> additionally(a<b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity);
Ответ: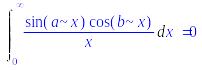
Численно найти интеграл
.
> restart;
> Int(sin(3*x)*exp(-1*x^2)/x^4, x=0.1..0.2)= evalf(int(sin(3*x)*exp(-1*x^2)/x^4, x=0.1..0.2));
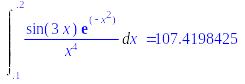
Ответ:
Полностью проделать все этапы вычисления интеграла
по частям
> restart;
> f:=x^3*cos(x);
> with(student):J:=Int(f,x=0..Pi/2);
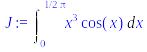
> J:=intparts(Int(f,x=0..Pi/2),x^3);
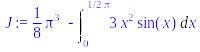
> intparts(%,x^2);
> intparts(%,x);
> value(%);
Ответ:
Вычислить интеграл
с помощью универсальной подстановки
tg(x/2)=t.
> restart;
> with(student):
> J=Int(1/(5-4*sin(x)+3*cos(x)), x=0..Pi/2);
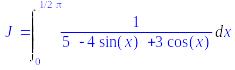
> J=changevar(tan(x/2)=t,Int(1/(5-4*sin(x)+3*cos(x)), x=0..Pi/2),t);
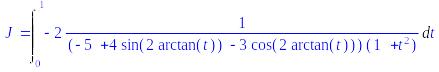
> value(%);
Ответ:
Вычислить тройной интеграл:
.
> restart: with(student):
> J:=Tripleint(ln(z-x-y)/((x-exp)*(x+y-exp)),x=exp..x+y+exp, y=0..exp-x-1, z=0..exp-1);
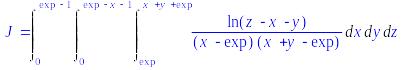
> value(%);
Ответ:
7.Найти изображения Лапласа и построить их графики для следующих функций:
а)
;
б)
.
> restart;
> with(inttrans):
> F(p):=laplace(sin(t)/t,t,p);
Ответ:
> plot(F(p),p);
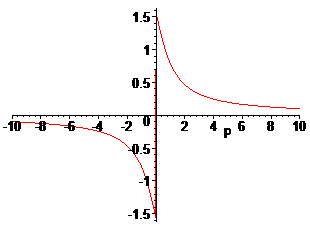
> restart;
> with(inttrans):
> F(p):=laplace(((1-cos(2*t))*exp(-3*t))/t,t,p);
Ответ:
> plot(F(p),p);
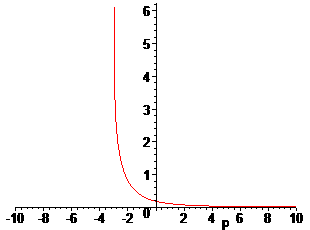
8.
Найти оригинал
Лапласа функции
и построить его график.
> restart;
> with(inttrans):
> F(x):=invlaplace(1/(((p-1)^2)*(p^2+1)),p,x):
> combine(%,trig);
Ответ:
> plot(F(x),x);
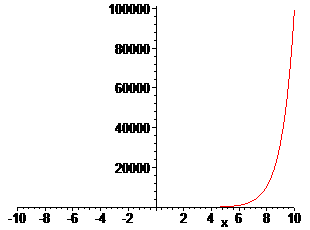
9.Дана
функция
,
найти ее изображение Лапласа.
> restart;
> f(x):=int((1-cos(x*t))/x^2,x=0..+infinity);
> with(inttrans):
> F(p):=laplace(f(x),t,p);
> plot(F(p),p);
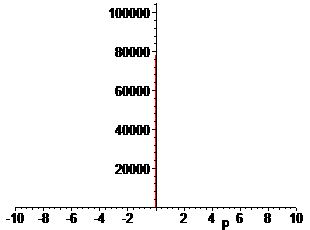
Контрольные вопросы.
Что такое команды прямого и отложенного исполнения? Опишите их действия.
Прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования – вычисляет интеграл;
Отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int – выдает на экран интеграл в аналитическом виде математической формулы.
Какие команды производят аналитическое и численное интегрирование? Опишите их параметры.
int(f, x), где f – подынтегральная функция, x – переменная интегрирования (для вычисления определенного интеграла добавляются пределы интегрирования)
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования.
Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число знаков после запятой).