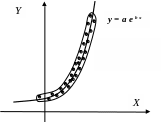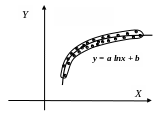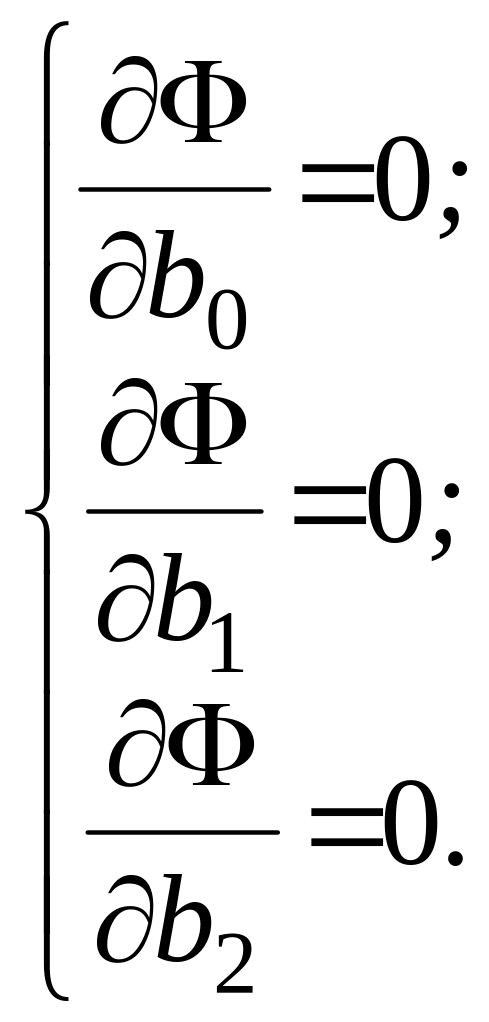- •Орієнтовний перелік питань для підсумкового контролю знань
- •Тема 1. Математичне моделювання як метод наукового пізнання економічних явищ і процесів
- •1.1 Економетрика як наука, об’єкт, предмет, мета та задачі. Основні характеристики економічної системи як об’єкта моделювання
- •1.2 Поняття моделі. Математична модель, основні етапи процесу моделювання, класифікація моделей
- •Етапи проведення економетричних досліджень
- •Тема 2. Моделі парної регресії та їх дослідження
- •2.1 Приклади парних зв’язків в економіці
- •Модель споживання
- •Модель пропозиції та попиту
- •Найпростіша кон'юнктурна модель (модель Кейнса)
- •Виробнича функція Кобба-Дугласа
- •2.2 Парна регресія
- •2.2.1 Специфікація моделі
- •2.2.2 Визначення параметрів рівняння регресії за допомогою методу найменших квадратів
- •Тема 3. Загальна лінійна економетрична модель
- •3.1 Загальний вид лінійної економетричної моделі, її структура та етапи побудови
- •3.2 Деяка інформація про випадкові збудники
- •3.3 Умови Гауса-Маркова. Гомоскедастичні та гетероскедастичні моделі
- •Тема 4. Лінійна парна регресія
- •4.1 Загальний вид лінійної парної моделі
- •4.2 Визначення оцінок параметрів парної лінійної регресії за допомогою мнк
- •4.3 Властивості оцінок, а також залишків мнк, їх характеристика
- •4.4 Аналіз рівнянь лінійної регресії і властивості вибіркового коефіцієнту кореляції
- •4.5 Дисперсійний аналіз та поняття коефіцієнта детермінації, його властивості
- •Властивості коефіцієнта детермінації
- •4.6 Перевірка лінійної моделі на адекватність. Поняття -критерію Фішера
- •4.7 Перевірка значимості параметрів регресійної моделі та коефіцієнту кореляції
- •4.8 Побудова інтервалів довіри для параметрів регресійної моделі
- •4.9 Зона довіри для лінії регресії
- •4.10 Прогноз і інтервал довіри для прогнозу
- •4.11 Коефіцієнт еластичності
- •Тема 5. Нелінійна парна регресія
- •5.1 Загальні відомості
- •5.2 Метод лінеаризації
- •5.3 Методи обчислення невідомих параметрів нелінійних моделей
- •5.4 Перевірка адекватності квадратичного рівняння регресії
- •5.5 Довірчий інтервал і прогноз для нелінійної моделі
- •5.6 Коефіцієнти еластичності для нелінійних моделей
- •5.7 Аналіз монопольного ринку
- •Коефіцієнт еластичності попиту
- •Тема 6. Множинна регресія
- •6.1 Загальні відомості
- •6.2 Вибір та аналіз усіх можливих факторів, які впливають на процес або показник, що досліджується
- •6.2.1 Поняття про мультиколінеарність та її вплив на оцінки параметрів моделі
- •6.2.2 Порядок виявлення та усунення мультиколінеарності
- •6.2.3 Виявлення мультиколінеарності в масиві факторів за допомогою алгоритму Фаррара-Глобера
- •6.2.4 Алгоритм усунення мультиколінеарності
- •6.3 Вибір виду рівняння регресії
- •6.4 Загальна модель множинної лінійної регресії
- •6.5 Емпірична модель множинної лінійної регресії
- •6.6 Визначення коефіцієнтів рівняння множинної лінійної регресії
- •6.7 Перевірка адекватності множинної регресійної моделі
- •6.8 Прогноз і довірчий інтервал для прогнозу множинної регресії
- •Тема 7. Економетричні моделі динаміки
- •7.1 Методи моделювання часових рядів
- •7.2 Автокореляція часового ряду
- •Властивості коефіцієнта автокореляції
- •7.3 Моделювання тенденції часового ряду: згладжування та аналітичне вирівнювання
- •7.4 Автокореляція залишків в множинній регресії
- •7.4.1 Поняття про автокореляцію залишків, її природа, причини виникнення і наслідки
- •7.4.2 Визначення наявності автокореляції залишків
- •Алгоритм тесту Дарбіна-Уотсона
- •Обмеження на застосування критерія Дарбіна-Уотсона
- •Словник
- •Рекомендована література Основна:
- •Додаткова:
2.2.1 Специфікація моделі
Найбільш очевидним
є вибір специфікації моделі у випадку
парної регресії, оскільки його можна
виконати візуально, використовуючи
графічне зображення емпіричних даних
як точок
![]() на кореляційному полі в декартовій
системі координат, які утворюють так
звану діаграму розсіювання.
на кореляційному полі в декартовій
системі координат, які утворюють так
звану діаграму розсіювання.
У випадках, коли кореляційне поле вказує на те, що пряма лінія не підходить для опису характеру залежності, застосовуються складніші види залежності, а саме – нелінійна регресія. Форма цієї залежності може бути різною. Залежно від того, яке рівняння обирається, регресія отримує відповідну назву (рис. 2.6).
|
|
а) квадратична регресія |
б) експоненційна регресія |
|
|
в) логарифмічна регресія |
г) степенева регресія |
Рисунок 2.6 – Приклади нелінійних видів регресій
Для множинної регресії виявлення залежності між змінними значно ускладнюється. Тут в деяких випадках може спрацювати інтуїція.
2.2.2 Визначення параметрів рівняння регресії за допомогою методу найменших квадратів
Після того, як вид рівняння регресії вибраний, формула для опису лінії регресії підібрана, виникає друга проблема – потрібно оцінити параметри, які увійшли до нього.
У записане рівняння обов'язково входять коефіцієнти (параметри), і ці коефіцієнти потрібно визначити. Причому зробити це так, щоб побудоване рівняння найкращим чином описувало дані спостережень, щоб лінія регресії проходила якомога ближче до точок кореляційного поля. Цей етап має назву статистичної оцінки параметрів регресії.
Наприклад, на рис. 2.7 зображено випадок, коли кореляційне поле показує, що можна застосувати лінійну регресію.

Рисунок 2.7 – Приклад кореляційного поля
У рівняння
прямої
![]() входять два параметри:
входять два параметри:
![]() і
і
![]() .
Змінюючи їх, отримуємо різні прямі
лінії, з яких необхідно вибрати тільки
одну, з конкретними значеннями параметрів
(в даному випадку ту, яка на рис. 2.7
зображена під номером 4).
.
Змінюючи їх, отримуємо різні прямі
лінії, з яких необхідно вибрати тільки
одну, з конкретними значеннями параметрів
(в даному випадку ту, яка на рис. 2.7
зображена під номером 4).
У загальному випадку задача для трьох невідомих факторів формулюються таким чином. Для обраної формули рівняння регресії
|
(2.29) |
необхідно підібрати параметри регресії так, щоб відхилення даних спостережень від лінії регресії були б мінімальними.
Для вирішення цієї задачі є декілька методів. Найпопулярніший і найчастіше використовуваний з них – метод найменших квадратів (МНК). Щоб визначити ступінь відхилення кривої від експериментальних точок (або навпаки, експериментальних точок від кривої регресії) введемо наступне визначення.
Відхиленням (або
залишком) називається різниця між
експериментальним значенням
![]() і теоретичним значенням
і теоретичним значенням
![]() :
:
|
(2.30) |
Тут
![]() – дані спостережень, відомі числа.
Покажемо ці відхилення на рис. 2.8:
– дані спостережень, відомі числа.
Покажемо ці відхилення на рис. 2.8:
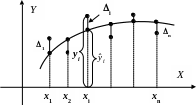
Рисунок 2.8 – Відхилення
Знаходження оцінок МНК геометрично означає пошук функції, яка знаходиться найближче до даних точок (статистичних даних) у тому розумінні, що сума квадратів відстаней по вертикалі від даних точок до функції повинна бути найменшою. Обґрунтування такого вибору методу побудови оцінок полягає в їх оптимальних статистичних властивостях, які сформульовано вище.
Всі ці відхилення повинні бути якомога менші. Цього можна досягти, якщо узяти суму квадратів цих чисел і зажадати, щоб вона була мінімальна:
|
(2.31) |
Тобто, сума квадратів відхилень є функцією від коефіцієнтів регресії, а отже необхідно знайти мінімум функції декількох змінних. З курсу вищої математики відомо, що для цього необхідно знайти частинні похідні і прирівняти їх нулю:
|
(2.32) |
Отримаємо
систему рівнянь для знаходження
коефіцієнтів регресії. Скільки
коефіцієнтів присутньо в рівнянні
регресії, стільки буде і рівнянь в цій
системі. Ця система називається нормальною
системою
для визначення коефіцієнтів регресії.
В результаті її розв’язання отримаємо
коефіцієнти регресії
![]() .
.
Докладніше процес складання і розв’язання цієї системи буде розглянуто нижче для рівняння лінійної регресії.