7.4 Автокореляція залишків в множинній регресії

7.4.1 Поняття про автокореляцію залишків, її природа, причини виникнення і наслідки

В економетрічних дослідженях часто виникають ситуації, коли дисперсія відхилень – стала, але спостерігається коваріація відхилень. Одним з основних припущень класичного лінійного регресійного аналізу, починаючи з нормальної системи рівнянь і закінчуючи довірчим інтервалом, є припущення щодо відсутності взаємозв’язку між значеннями стохастичної складової моделі в різних спостереженнях, тобто припущення, що залишки є лінійно незалежними і підпорядковуються нормальному закону розподілу з математичним сподіванням, яке дорівнює нулю:

, .

(7.5)

Якщо це припущення порушується – виникає явище, яке носить назву автокореляції залишків. В цьому випадку побудоване рівняння регресії буде неадекватне.

Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.

Іншими словами, автокореляція залишків – це кореляція ряду з рядом , де характеризує запізнення. Кореляція між сусідніми членами ряду ( ) називається автокореляцією першого порядку.

Автокореляція залишків найчастіше спостерігається у наступних двох випадках:

1. коли економетричну модель будують на основі часових рядів (у цьому випадку, якщо існує кореляція між послідовними значеннями деякої незалежної змінної, то буде спостерігатися і кореляція між послідовними значеннями стохастичної складової , особливо, якщо використовуються лагові змінні);

2. коли допущена помилка специфікації економетричної моделі – до моделі не включена істотна пояснююча змінна, а отже рівняння регресії підібрано невірно.

При оцінювані параметрів економетричної моделі методом найменших квадратів без врахування наявності автокореляції відхилень можливі такі наслідки:

1 . Оцінки параметрів моделі будуть зміщеними, неефективними. Неефективність оцінок параметрів приводить до прогнозу, який може мати велику вибіркову дисперсію.

2. В дисперсійному аналізі не можна застосувати статистичні критерії Стьюдента та Фішера.

7.4.2 Визначення наявності автокореляції залишків

Оскільки автокореляція є негативним явищем, потрібно вміти його визначати. На даний час найбільш розповсюдженими тестами, які використовуються для визначення автокореляції залишків, є наступні статистичні тести:

1. тест Дарбіна-Уотсона;

2. тест фон Неймана;

3. тест на основі нециклічного коефіцієнта автокореляції;

4. тест на основі циклічного коефіцієнта автокореляції.

Найбільш відомим і поширеним способом перевірки моделі на наявність автокореляції залишків є тест Дарбіна-Уотсона. Цей тест використовується для авторегресійних схем 1-го порядку і має наступний алгоритм.

Алгоритм тесту Дарбіна-Уотсона

Крок 1. Висуваються гіпотези:

– автокореляція в залишках відсутня;

– наявність додатньої автокореляції;

– наявність від’ємної автокореляції.

Крок 2. Виходячи з відсутності автокореляції залишків на основі методу найменших квадратів будується економетрична модель і обчислюються її залишки ( ).

Крок 3. Розраховується статистика (критерій) Дарбіна-Уотсона за наступною залежністю:

.

(7.6)

Ця статистика може приймати будь-яке значення з інтервалу (0,4).

Між статистикою і коефіцієнтом автокореляції існує приблизна залежність:

,

(7.7)

де – коефіцієнт автокореляції першого порядку, який позначають наступним чином:

.

При відсутності автокореляції і -статистика приймає значення близьке до 2.

Властивості -статистики і коефіцієнта автокореляції :

1. Якщо і , то в залишках існує повна додатня автокореляція.

2. Якщо і , то в залишках існує повна від’ємна автокореляція.

3. Якщо і , то в залишках не існує автокореляції.

Отже, якщо , то і автокореляція додатня. Також із перелічених властивостей витікає, що:

.

Графічно випадки додатньої і від’ємної автокореляції залишків, а також її відсутності можна представити наступним чином (рис. 7.4):

Рисунок 7.4 – Графічна ілюстрація автокореляції залишків

Крок 4. Задаючись рівнем значимості , для числа факторів моделі і числа спостережень за статистичними таблицями розподілу Дарбіна-Уотсона, визначаються критичні значення: нижня межа і верхня межа . Критичні межі -статистики дозволяють з заданою надійністю робити висновок про наявність або відсутність автокореляції першого порядку.

Крок 5. Відрізок розбивають на 5 частин і будуються зони автокореляційного зв’язку, які схематично можна представити в виді, наведеному на рис. 7.5.

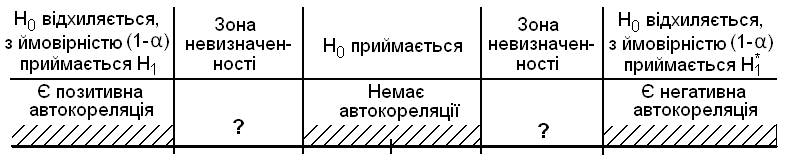
Рисунок 7.5 – Зони автокореляційного зв’язку

Якщо розрахункове значення потрапляє в зону невизначеності, то це означає, що статистичних даних недостатньо, щоб зробити висновок. На практиці, якщо потрапляє в зону невизначеності, то припускають існування автокореляції залишків і гіпотезу відхиляють.

Крок 5. На основі розрахункового значення критерію роблять висновок щодо наявності або відсутності автокореляції залишків:

• якщо – це свідчить про наявність позитивної автокореляції залишків;

• якщо – це свідчить про наявність негативної автокореляції залишків;

• якщо або – неможливо зробити висновок ні про наявність, ні про відсутність автокореляції залишків;

• якщо – автокореляція залишків відсутня.