6.2 Вибір та аналіз усіх можливих факторів, які впливають на процес або показник, що досліджується

Фактори, які включаються в множинну регресію, повинні відповідати наступним вимогам:

• вони повинні бути кількісно вимірні: якщо необхідно включити в модель якісний фактор, який не має кількісного виміру, то йому необхідно придати кількісну визначеність;

• фактори не повинні бути інтеркорельовані і тим більше не повинні знаходитися в точному функціональному зв’язку.

Інтеркореляція – кореляція між пояснюючими змінними.

Включення в модель факторів з високою інтеркореляцією може привести до небажаних наслідків – система нормальних рівнянь може опинитися поганообумовленою і спричинити за собою нестійкість і ненадійність оцінок коефіцієнтів регресії.

Якщо між факторами існує висока кореляція, то неможливо визначити їх ізольований вплив на результативний показник.

Таким чином, незважаючи на те, що теоретично регресійна модель може включати будь-яке число факторів, практично в цьому немає необхідності. відбір факторів проводиться на основі якісного теоретико-економічного аналізу в дві стадії. На першій підбираються фактори виходячи із суті проблеми. На другій – на основі кореляційної матриці визначають наявність лінійної залежності між пояснюючими змінними.

При побудові множинної регресії коефіцієнти кореляції можна розрахувати для кожної пари факторів, які входять в модель. Тоді кожен елемент кореляційної матриці представляє собою саме парний коефіцієнт кореляції між відповідними факторами:

.

(6.2)

Кореляційна матриця є квадратною, симетричною відносно головної діагоналі, розмірністю , де – число факторів , які включені в модель.

Парні коефіцієнти кореляції розраховуються за формулою:

.

(6.3)

Зв’язок між факторами і характеризується коефіцієнтом кореляції і теж утворює матрицю розмірністю :

.

(6.4)

Для того, щоб побудувати кореляційні матриці, необхідно провести стандартизацію початкових статистичних даних – всі фактори повинні бути кількісно сумірні, тому їх нормують і приводять до безрозмірних величин. Всі початкові дані перераховуються за формулами наведеними нижче і вводяться нові величини.

Всі початкові фактори необхідно перерахувати за формулою:

.

(6.5)

Результуючий фактор перераховується за формулою:

.

(6.6)

Тут , – обсяг вибірки, – число факторів.

Після стандартизації всі фактори стають безрозмірними і такими, що можна порівняти їх величини. Використовуючи матричні перетворення кореляційні матриці можна отримати у вигляді:

; .

(6.7)

6.2.1 Поняття про мультиколінеарність та її вплив на оцінки параметрів моделі

Суть мультиколінеарності полягає в тому, що в багатофакторній регресійній моделі дві або більше незалежних змінних пов'язані між собою лінійною залежністю або, іншими словами, мають високий ступінь кореляції: .

Мультиколінеарність означає існування тісної лінійної залежності, або сильної кореляції, між двома і більше факторними змінними.

Відсутність мультиколінеарності означає, що ніяка з пояснювальних змінних не може бути зображена у вигляді лінійної комбінації решти змінних. Це можна пояснити на прикладі діаграми (рис. 6.1).

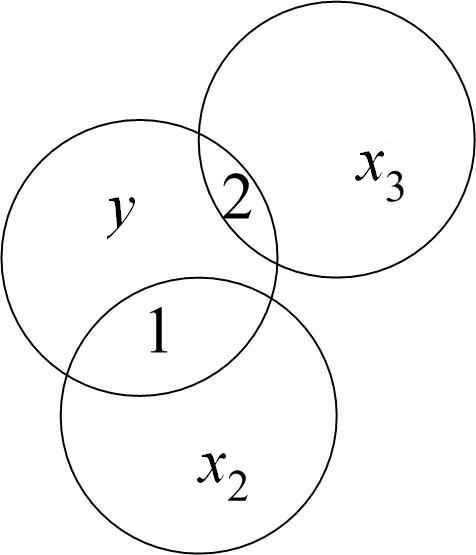
а) б)

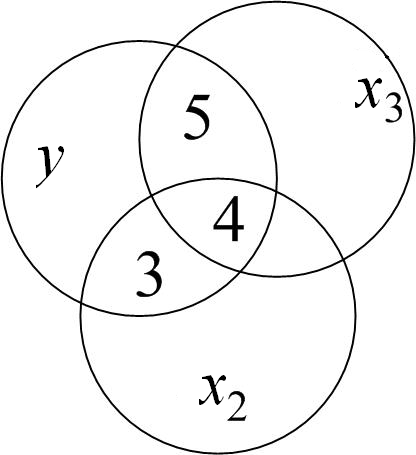
Рисунок 6.1 – Діаграма, що демонструє відсутність (а) і наявність мультиколінеарності (б)

На рис. 6.1 коло зображає варіацію залежної змінної , а кола і зображають, відповідно, варіації регресорів і . На рис. 6.1 а) область 1 зображає варіацію в , пояснену за рахунок , а область 2 – варіацію в , пояснену за рахунок . Області 3 і 4 (рис. 6.1 б) зображають варіацію в , пояснену через , а області 4 і 5 – пояснену через . Але, оскільки область 4 є загальною для і , не можливо назвати а priori, яка частина 4 належить , а яка – . Загальна область 4 представляє випадок мультиколінеарності. Гіпотеза відсутності мультиколінеарності вимагає відсутності перекриття між і , тобто загальна область 4 повинна бути нульовою. Іншими словами, завжди необхідно мати справу із ситуацією, зображеною на рис. 6.1 а).

Формально відсутність мультиколінеарності означає, що немає таких чисел і , які одночасно не є нулями, що

.

(6.8)

Якщо ж подібне лінійне співвідношення виконується, тоді говорять, що і колінеарні або лінійно залежні. Якщо ж (6.8) виконується тільки при і , то говорять, що і лінійно незалежні.

Так, якщо

або ,

то дві змінні лінійно залежні, і якщо обидві вони включені в регресійну модель, матимемо точну мультиколінеарність або точну лінійну залежність між двома змінними.

Припустимо тепер, що . Чи буде при цьому порушена гіпотеза відсутності мультиколінеарності? Ні, оскільки зв’язок між регресорами нелінійний і не порушується вимога про відсутність лінійного зв’язку між регресорами.

Мультиколінеарність – це поняття, яке використовується для опису проблеми, коли нестрога лінійна залежність між пояснювальними змінними призводить до отримання ненадійних оцінок регресії. Проте, така залежність зовсім необов’язково дає незадовільні оцінки. Якщо всі інші умови задовільні, тобто якщо кількість спостережень і вибіркові дисперсії пояснювальних змінних великі, а дисперсія випадкового члена – мала, то в результаті можна отримати досить позитивні оцінки.

Мультиколінеарність повинна виникати за рахунок сполучення нестрогої залежності однією (або більше) незадовільних умов, це – питання ступеня визначеності явища, а не його виду. Оцінки регресії будуть неадекватні від неї у відповідній мірі значущості. Розгляд цієї проблеми починається тільки тоді, коли вона досить суттєво впливає на результати оцінки регресії.

Зауваження. Мультиколінеарність не є проблемою, якщо єдиною метою регресійного аналізу є прогноз (оскільки чим більше значення , тим точніший прогноз). Якщо метою аналізу є не прогноз, а дійсне значення параметрів, то мультиколінеарність перетворюється на проблему, оскільки її наявність призводить до значних стандартних похибок оцінок параметрів.

Підводячи підсумки зазначимо, що гіпотеза про відсутність мультиколінеарності вимагає, щоб у функцію включали тільки ті змінні, які не є лінійними функціями деяких інших змінних моделі.