Коефіцієнт еластичності попиту
Розглянемо також величину, яка називається коефіцієнтом еластичності попиту:
|
(5.25) |
.
Це число показує,
на скільки відсотків змінюється попит
при зростанні ціни на 1%.
Так як ціна
і попит
завжди позитивні, знак
визначається знаком похідної. Для
переважної більшості товарів попит
падає з ростом ціни, і значить похідна
негативна. А значить, негативним буде
і коефіцієнт еластичності
.
Існує таке поняття, як еластичність і нееластичність попиту. При цьому характер попиту визначається реакцією доходу на зміну ціни.
Попит нееластичний, якщо зі зростанням ціни дохід теж зростає; попит еластичний, якщо зі зростанням ціни дохід зменшується.
Зростання або убування доходу визначається знаком похідної:
|
(5.26) |
.
У залежності від
знаку
можливі наступні
варіанти величини коефіцієнта еластичності
(рис. 5.3, 5.4):
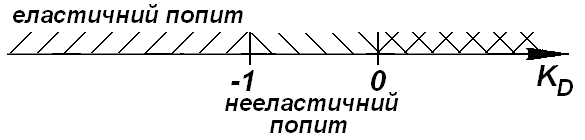
Рисунок 5.3 – Шкала коефіцієнту еластичності
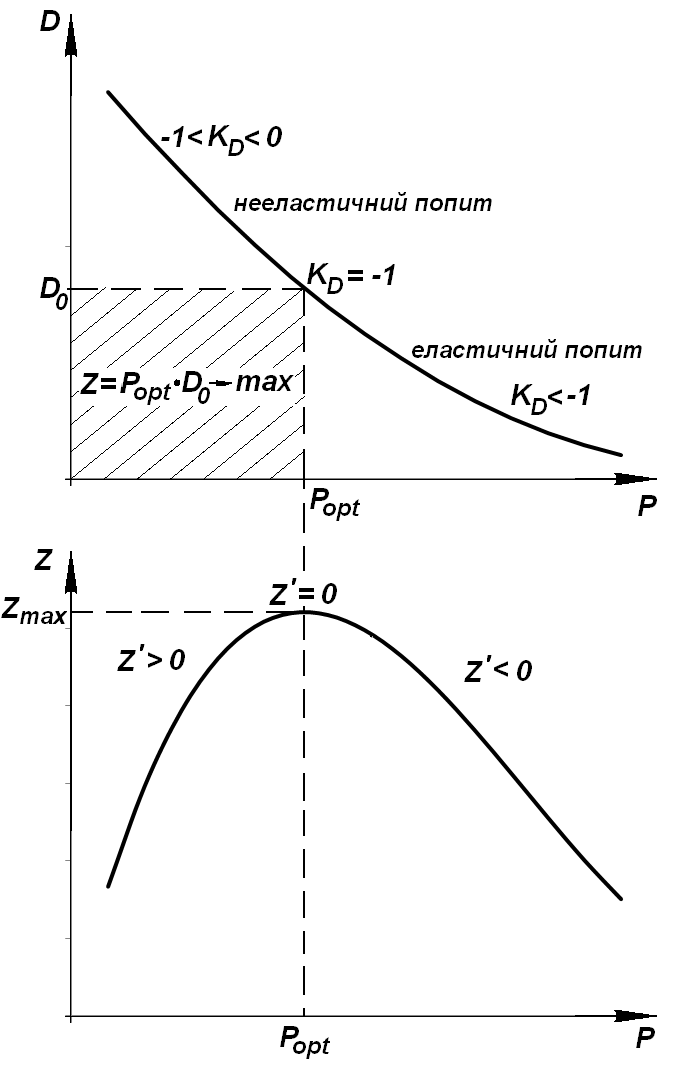
Рисунок 5.4 – Залежності попиту і доходу від ціни
1. Похідна
:
,
так як
,
то
.
Тобто на проміжку, де дохід
збільшується –
.
З іншого боку, регресія попиту убуває,
отже
.
Тобто із зростанням
ціни незважаючи на зниження попиту
дохід продовжує зростати і
.
В цьому випадку попит є нееластичним.
Економічна
інтерпретація: зміна ціни на 1% викликає
зміну попиту в зворотньому напрямку на
%,
де
.
При цьому с ростом ціни дохід зростає.
2. Похідна
:
,
так як
,
то
.
Тобто із зростанням ціни дохід падає
при одночасному зменшенні попиту і
.
В цьому випадку попит є еластичним.
Економічна інтерпретація: при еластичному попиті зміна ціни товару на 1% визиває зміну попиту на %, де .
3. Похідна
:
на цьому проміжку дохід постійний. При
цьому точка, в якій
,
–
– критична точка. Коефіцієнт еластичності
при цьому значенні ціни
.
Саме при цій ціні буде максимальним
дохід.
Залежність коефіцієнта еластичності від ціни для прийнятого випадку квадратичної регресії:
|
.Остаточно маємо:
|
(5.27) |
.Тема 6. Множинна регресія
6.1 Загальні відомості
Парна регресійна модель може дати гарний результат при моделюванні, якщо впливом інших факторів, які впливають на об’єкт дослідження, можна знехтувати.
В реальних
економічних зв’язках на будь-який
економічний показник
,
як правило, впливає не один, а декілька
факторів (регресорів)
.
Так, наприклад, попит населення на певний
товар буде визначатися не тільки ціною
на нього, але й цінами на його замінники,
доходами споживачів й іншими факторами.
У низці досліджень аналізується зв’язок
доходу працівника певної галузі
виробництва з його рівнем освіти, віком,
стажем роботи в цій галузі.
Тому слід виявити вплив інших факторів на результуючий , поширити просту модель з двома змінними на випадок з великою кількістю змінних і побудувати рівняння множинної регресії. Отже, постає задача виявлення статистичного взаємозв’язку між та .
Саме багатофакторний регресійний аналіз допомагає знайти явний вид залежності досліджуваного показника від численних факторів, які впливають на його зміну, а також кількісно оцінити їх вплив.
Множинною регресією називається рівняння зв’язку між результативною ознакою (залежною змінною) і факторними ознаками (незалежними, пояснюючими) .
Класичним прикладом множинної регресії є сучасна функція споживання:
|
(6.1) |
,
де
– споживання;
– дохід,
– ціна,
– готівкові гроші,
– ліквідні активи.
Множинна регресія широко використовується при розв’язку проблем попиту, дохідності акцій, при вивченні функцій витрат виробництва в макроекономічних розрахунках і цілого ряду інших питань економетрики.
В теперішній час множинна регресійний аналіз – це один із найбільш поширених методів в економетриці.
Основна мета множинної регресії – побудувати модель з великим числом факторів, визначивши при цьому вплив кожного з них окремо, а також їх сукупний вплив на показник, який моделюється.
Побудова рівняння множинної регресії починається з вирішення двох питань – відбору факторів і вибору виду рівняння регресії.