4.9 Зона довіри для лінії регресії
Рівняння регресії
– це теж не істинне рівняння, а лише
приблизне знання про нього. І підраховані
за ним теоретичні значення фактора
,
тобто
– теж.
Справжні значення із заданою вірогідністю
γ лежать в зоні довіри
.
Ця зона утворюється гіперболами, які
розташовані по обидві сторони від лінії
регресії.
Для побудови
довірчої зони для лінії регресії
необхідно знати стандартну помилку
:
|
(4.35) |
,
де .
Тоді розмах довірчої зони визначається формулою:
|
(4.36) |
.А границі довірчої зони лінії регресії:
|
(4.37) |
.
Отже, якщо підрахувати
ці значення
і відступити від лінії регресії на
відповідні відстані вгору і вниз, то
отримаємо довірчу зону для лінії
регресії. Справжня лінія регресії із
заданою вірогідністю γ повинна знаходитися
в межах цієї довірчої зони.
4.10 Прогноз і інтервал довіри для прогнозу
Якщо побудована модель регресії адекватна, то можна використовувати це рівняння для прогнозування, тобто знаходити прогнозні значення залежної змінної виходячи із моделі. При цьому можна отримати два типи прогнозів: точкові та інтервальні.
Точковий прогноз
дає значення залежної змінної для
відповідного значення незалежної
змінної. Прогнозне значення
визначається шляхом підстановки в
рівняння регресії прогнозного значення
:
|
(4.38) |
.
Виходячи з отриманого
точкового прогнозу, можна побудувати
інтервали довіри для прогнозного
значення. Для цього необхідно розрахувати
середню стандартну похибку прогнозу
:
|
(4.39) |
.Формули для розрахунку інтервалу довіри для прогнозного значення мають наступний вид:
|
(4.40) |
,
де
.
4.11 Коефіцієнт еластичності
Коефіцієнт еластичності показує на скільки зміниться результуючий фактор , якщо незалежний фактор зміниться на 1%.
Формула розрахунку коефіцієнта еластичності:
|
(4.41) |
,
де
– рівняння, що визначає форму зв’язку
між змінними;
– перша похідна
рівняння, яка характеризує співвідношення
приростів результату і фактора для
відповідної форми зв’язку.
Для лінійної регресії коефіцієнт еластичності можна знайти наступним чином:
|
(4.42) |
.В силу того, що коефіцієнт еластичності для лінійної функції не є величиною постійною, а залежить від відповідного значення , то звичайно розраховується середній показник еластичності за формулою:
|
(4.43) |
.Тема 5. Нелінійна парна регресія
5.1 Загальні відомості
Залежності між чинниками та результуючими показниками у багатьох економічних задачах є набагато складніші за ті, що можуть відображатися лінійними функціями. Це призводить до необхідності розгляду нелінійних регресійних моделей.
За методикою оцінок параметрів нелінійні регресії розглядають двох видів.
1. Квазілінійні регресії – залежності, які є нелінійними щодо включених в аналіз пояснюючих змінних, але лінійні щодо параметрів, які треба оцінити за статистичними даними (нелінійні за факторами і лінійні за коефіцієнтами).
Наприклад:
,
,
.
У всіх цих співвідношеннях коефіцієнти стоять у перших ступенях, тобто формули лінійні за коефіцієнтами.
2. Власне нелінійні регресії – залежності, які є нелінійними по відношенню до функції (нелінійні і за факторами, і за коефіцієнтами)
Наприклад:
,
,
,
.
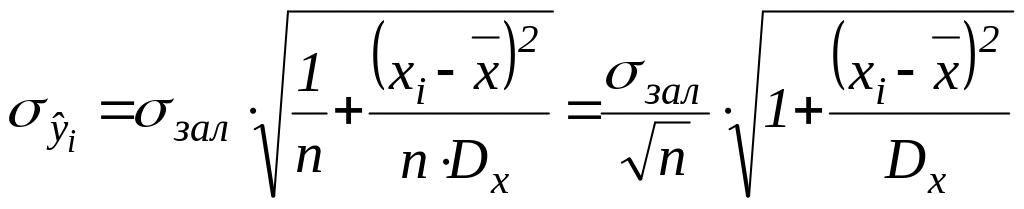
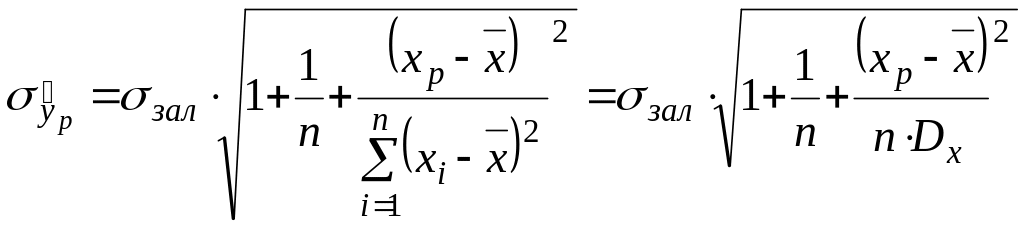