4.5 Дисперсійний аналіз та поняття коефіцієнта детермінації, його властивості

Поряд з коефіцієнтом кореляції використовується ще один критерій оцінки якості підбору лінійної функції, за допомогою якого перевіряється адекватність (відповідність) побудованої регресійної моделі реальній дійсності. Таким критерієм є коефіцієнт детермінації. Коефіцієнт детермінації характеризує будь-яку кореляційну залежність, (не обов'язково лінійної) тобто показує, наскільки розкидані статистичні дані навколо побудованої лінії регресії. В той час як коефіцієнт кореляції використовується для оцінки якості рівняння лінійної регресії. Якщо ж рівняння нелінійне, то аналогічну роль відіграє тільки коефіцієнт детермінації.

Перед тим, як розглянути, що саме являє собою коефіцієнт детермінації та як він пов’язаний з коефіцієнтом кореляції, розглянемо питання про декомпозицію дисперсій.

У статистиці різницю прийнято називати загальним відхиленням. Різницю називають відхиленням, яке можна пояснити, виходячи з регресійної прямої. Різницю називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснюваним відхиленням.

Завдання дисперсійного аналізу полягає в аналізі дисперсії залежної змінної:

,

(4.23)

де – загальна сума квадратів відхилень;

– сума квадратів похибок;

– сума квадратів відхилень, що пояснює регресію.

Загальну дисперсію можна розкласти на дві частини: дисперсію, що пояснює регресію, та дисперсію похибок. Перша виникає завдяки розкиду значень незалежної змінної. Тобто, ця частина пояснюється за рахунок моделі (звідси і назва – пояснена сума квадратів). Друга частина – сума квадратів залишків – виникає внаслідок збурень і не пояснюється за рахунок моделі. Умовно це можна записати у вигляді:

,

(4.24)

де – загальна дисперсія;

– дисперсія, що пояснює регресію;

– дисперсія залишків, яка характеризує розкид даних спостережень відносно лінії регресії;

– об’єм вибірки;

– число параметрів при змінних , що включено в регресійну модель.

Частина дисперсії, що пояснює регресію, називається коефіцієнтом детермінації і позначається . Коефіцієнт детермінації використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної. Він показує, яка доля загальної варіації ознаки визначається фактором, що вивчається, тобто характеризує долю дисперсії результативної ознаки , що пояснюється регресією, в загальній дисперсії результативної ознаки.

Таким чином, коефіцієнт детермінації можна записати у вигляді двох виразів, які є еквівалентними:

.

(4.25)

В (4.25) у чисельнику стоять теоретичні значення , які підраховуються за побудованою теоретичної формулою – за рівнянням регресії, а у знаменнику – дані спостережень .

В ідеальному випадку, коли всі дані спостережень лежать точно на побудованій лінії регресії, теоретичні значення і дані спостережень просто співпадають. Чисельник в даному випадку буде дорівнювати знаменнику і коефіцієнт детермінації дорівнює 1.

Чим більший розкид даних спостережень щодо побудованої лінії регресії, тим менше значення коефіцієнта детермінації .

Якщо коефіцієнт детермінації визначається у відсотках, то його слід читати наступним чином: варіація залежної змінної на відсотків обумовлена варіацією фактора.
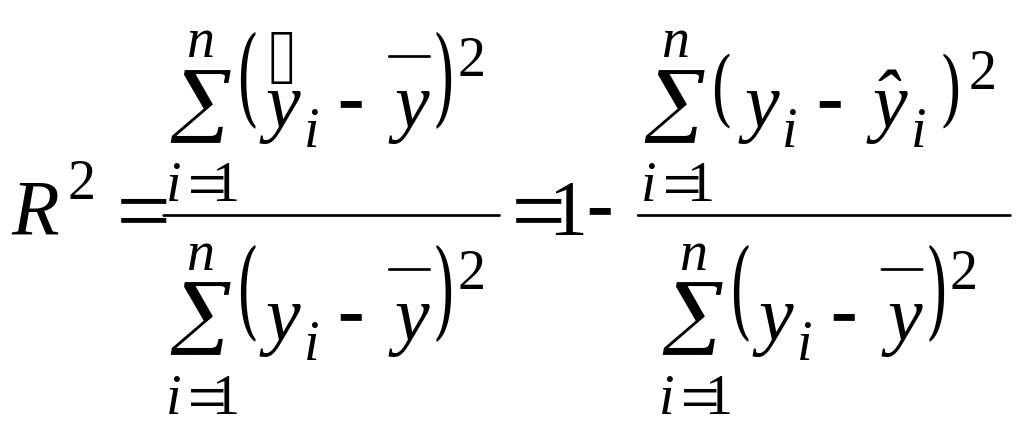