4.3 Властивості оцінок, а також залишків мнк, їх характеристика

В лінійній моделі (4.13) коефіцієнт (нахил) має назву коефіцієнту регресії, який показує середнє змінення результату при зміненні фактору на одну одиницю. Коефіцієнт регресії завжди має найменування. Якщо , то зв’язок між ознаками прямий, якщо , то зв’язок зворотній, якщо , то лінійний зв’язок відсутній.

Формально параметр – це початок відліку або значення при (тобто точка перетину з віссю ординат). Цей параметр може не мати економічного змісту, адже спроби економічно інтерпретувати цей параметр можуть привести до абсурду, особливо, якщо . Інтерпретувати можливо лише знак при параметрі . Якщо , то відносне змінення результату відбувається повільніше, ніж змінення фактору (варіація результату менше варіації фактору).

Отриманi результати, зокрема формули (4.11) i (4.12), дають змогу зробити ряд висновків.

1. Оцінки МНК є функціями від вибірки.

2. Оцінки МНК є точковими оцінками теоретичних коефіцієнтів регресії.

З. Вiдповiдно до формули (4.12) емпірична пряма регресії обов’язково проходить через точку .

4. Емпіричне рівняння регресії побудоване в такий спосіб, що сума відхилень (залишків) , а також середнє значення відхилення дорівнюють нулю:

, .

(4.18)

5. Випадкові відхилення некорельованi зi спостереженими значеннями залежної змінної .

6. Випадкові відхилення некорельовані зi спостереженими значеннями незалежної змінної i з оціненими за лінійною регресійною моделлю значеннями залежної змінної .

4.4 Аналіз рівнянь лінійної регресії і властивості вибіркового коефіцієнту кореляції

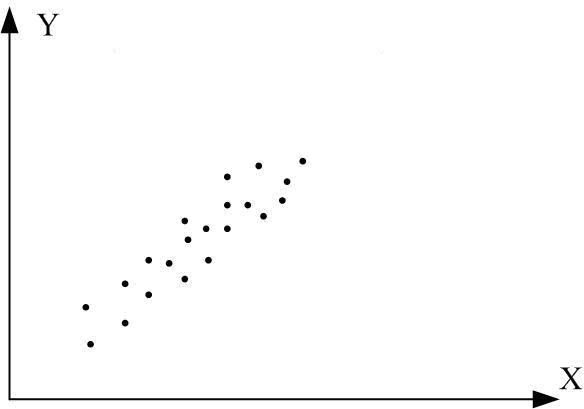
Знайдемо щільність зв’язку між залежною величиною і незалежною . Рівняння регресії завжди доповнюється показником, який характеризує ступінь щільності зв’язку між ознаками. Найпростішим критерієм, який дає кількісну оцінку зв’язку між двома показниками, при використанні лінійної регресії виступає вибірковий коефіцієнт кореляції (або лінійний коефіцієнт кореляції).

Лінійний коефіцієнт кореляції ( ) характеризує ступінь щільності лінійної кореляційної залежності, тобто показує наскільки розкидані експериментальні статистичні дані відносно прямої лінії регресії:

,

(4.19)

де – коефіцієнт коваріації, який характеризує не лише зв’язок між випадковими величинами і , а й їх розсіяння:

.

(4.20)

Підставивши (4.20) в (4.19), маємо:

.

(4.21)

Отже, вибірковий коефіцієнт кореляції характеризує ступінь вираженості лінійної залежності і .

Нагадаємо, що рівняння парної лінійної регресії можна представити в будь-якій з трьох форм запису:

Тип рівняння	Регресія на	Регресія на
Рівняння прямої з кутовим коефіцієнтом
Центроване рівняння (рівняння прямої,яка проходить через задану точку)
Стандартизоване рівняння

Структура цих рівнянь дозволяє зробити наступні висновки:

1. Обидві прямі проходять через точку з координатами і в цій точці перетинаються (рис. 4.2).

Рисунок 4.2 – Перетин прямих регресії

2. Розглянемо випадок, коли . При цьому обидва стандартизованих рівняння регресії матимуть вид: . Це означає, що прямі регресії співпадають – зливаються в одну. Це характерно для випадку, коли розкиду даних спостережень немає, а отже всі точки кореляційного поля лежать точно на одній прямій регресії (рис. 4.3).

Рисунок 4.3 – Співпадіння прямих регресій

В цьому випадку між і існує лінійна функціональна залежність.

3. Розглянемо випадок, коли . При цьому стандартизовані рівняння регресії приймають вид:

(4.22)

Це означає, що пряма регресії на горизонтальна, а на – вертикальна. Тобто, прямі регресії перпендикулярні одна одній і лінійний зв’язок у даному випадку відсутній. Це можливо у двох випадках: а) залежності між факторами немає взагалі (рис. 4.4 а); б) залежність є, і можливо дуже тісна, але вона не є лінійною (рис. 4.4 б).

а) б)

Рисунок 4.4 – Перпендикулярність прямих регресії

4. Знак показує якою є залежність – зростаючою чи спадаючою. Знак залежить від знака чисельника (4.19), що є мірою коваріації за вибіркою двох змінних:

– обидві прямі регресії зростаючі (додатня регресія),

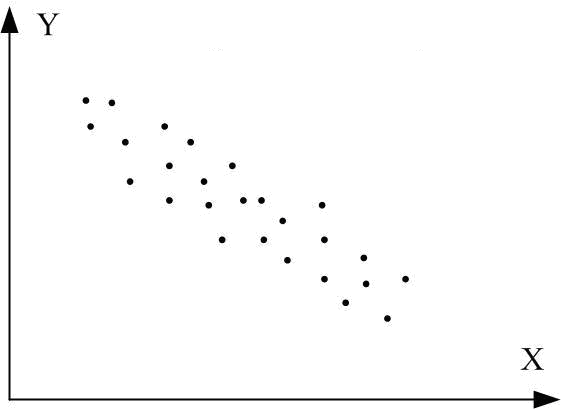
– обидві прямі регресії спадаючі (від’ємна регресія).

Отже, вибірковий коефіцієнт кореляції (при достатньо великому обсязі вибірки ) так же, як коефіцієнт кореляції двох випадкових величин має наступні властивості:

1. Коефіцієнт кореляції може бути додатнім або від’ємним. Знак біля значення коефіцієнта кореляції вказує на напрямок зв’язку: «+» – прямий, «–» – зворотній.

2. Коефіцієнт кореляції може приймати значення від –1 до 1, тобто або .

Чим ближче до нуля, тим більший розкид статистичних даних відносно прямої регресії, тим ця кореляційна залежність слабша.

Чим ближче до одиниці, тим менший розкид статистичних даних відносно прямої регресії, тим ця кореляційна залежність тісніша.

Якщо , то прямі регресії наближаються одна до іншої. Якщо , то прямі регресії віддаляються одна від іншої аж до перпендикулярності.

Чим ближче коефіцієнт кореляції до одиниці, тим зв’язок між ознаками щільніший:

– зв’язку немає;

– зв’язок слабкий;

– зв’язок помірний;

– зв’язок помітний;

– зв’язок сильний;

– зв’язок дуже сильний;

– зв’язок повний.

3. За своєю природою він симетричний, тобто коефіцієнт кореляції між і ( ) той же, що й між і ( ).

4. Він незалежний по відношенню до вибору початку системи координат і масштабу вздовж осей координат, тобто, якщо визначимо і , де , , , , і – константи, то коефіцієнт кореляції між і матиме те ж значення, що й між початковими змінними і .

5. Якщо і статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю, але якщо , це не означає, що дві змінні незалежні. Іншими словами, нульовий коефіцієнт кореляції не обов’язково означає незалежність (рис. 4.5 з).

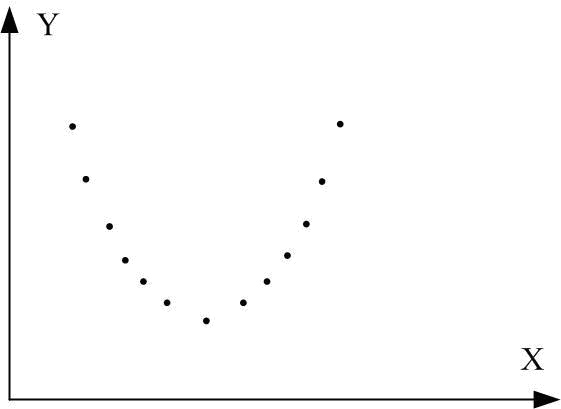
6. Коефіцієнт кореляції є мірою тільки лінійної асоціативності або лінійної залежності; він незастосовний для опису нелінійної залежності. Так, на рис. 4.5, з є точна залежність, хоча .

а)	б)
в)	г)
д)	є)
ж)	з)

Рисунок 4.5 – Кореляційний коефіцієнт для різних випадків вибірок

а) ; б) ; в) близький до 1; г) близький до –1;

д) додатній, близький до 0; є) r від’ємний, близький до 0; ж) ; з) 

7. Хоча є мірою лінійної асоціативності між двома змінними, це необов’язково означає який-небудь причинно-наслідковий зв’язок, як було відзначено раніше.
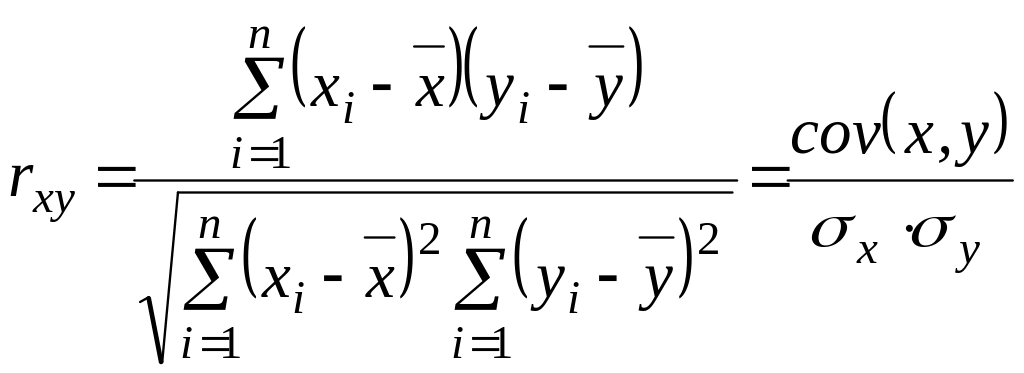