Тема 4. Лінійна парна регресія

4.1 Загальний вид лінійної парної моделі

Найпростішою серед лінійних економетричних моделей є модель парної лінійної регресії (або проста лінійна модель), яка описує зв’язок всього між двома економічними змінними – показниками.

Економетричною моделлю парної лінійної регресії (простою лінійною моделлю) називається регресійна модель, яка описує лінійний зв’язок між двома економічними показниками, один з яких є залежною (пояснюваною), а другий – незалежною (пояснюючою) змінною.

Виходячи з вищерозглянутих позначень для простої лінійної регресії маємо:

• теоретичну (“канонічну”) модель парної лінійної регресії:

  ;

  (4.1)

• вибіркову (емпіричну) модель парної лінійної регресії:

  ;

  (4.2)

• вибіркову функцію парної лінійної регресії:

.

(4.3)

Рівняння (4.3) представляє собою параметричне рівняння прямої, тому на площині вибірковій функції парної лінійної регресії відповідає вибіркова (емпірична) пряма регресії. Графічно вибіркова функція регресії і пряма регресії для деякої вибірки представлені на рис. 4.1.

yi ei  b0 Y x1 xi xn X

x1 y1 x2 y2 … … xi yi … … … … xn yn

Рисунок 4.1 – Парна лінійна регресія

Параметри моделі парної лінійної регресії мають спеціальну назву. Параметр називається перетином, а – нахилом. Математична інтерпретація цих параметрів зрозуміла з наведеного рисунку.

В економічних дослідженнях найбільш широке використання знайшли моделі лінійної регресії, хоча це і є спрощений засіб в моделюванні реальних економічних процесів. Ґрунтовне вивчення і застосування методики побудови лінійних моделей надає необхідну теоретичну базу для створення більш складних, нелінійних моделей, які в більшій мірі відповідають реальним економічним процесам. Якщо в рівняння включено лише одну пояснюючу змінну, то одержуємо теоретичну модель, яка дістала назву парної лінійної регресії:

.

(4.4)

Теоретичну модель для парної лінійної регресії можна записати наступним чином:

(4.5)

або у векторно-матричній формі, співвідношення (4.4) буде мати такий вид:

,

(4.6)

де

.

Для визначення теоретичних коефіцієнтів та необхідно буде використати всі значення ( ,  ) змінних і генеральної сукупності, що практично здійснити не можливо. Тому переходимо до побудови так званого емпіричного рівняння на базі інформації, одержаної із статистичної вибірки.

Емпіричне рівняння регресії має вид:

(4.7)

який аналогічно із теоретичною моделлю, запишемо у векторно-матричній формі:

,

(4.8)

де

.
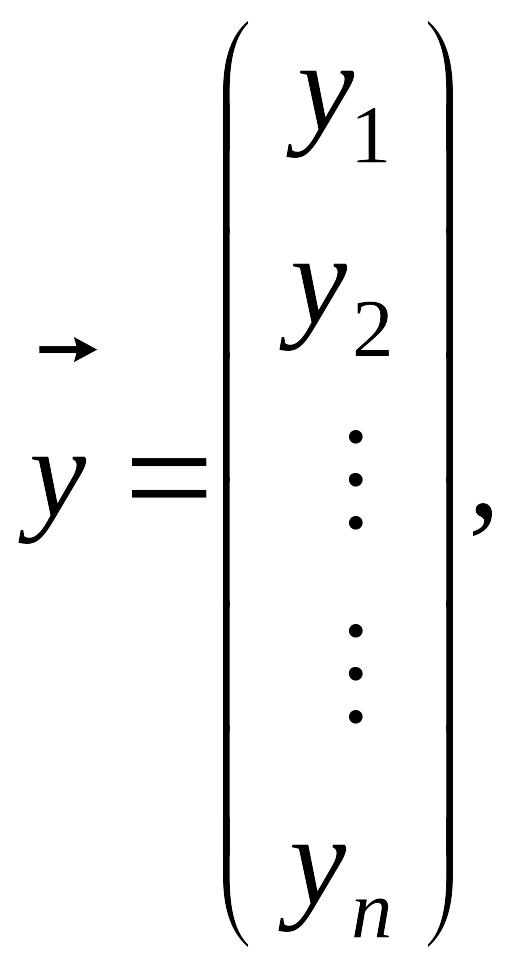
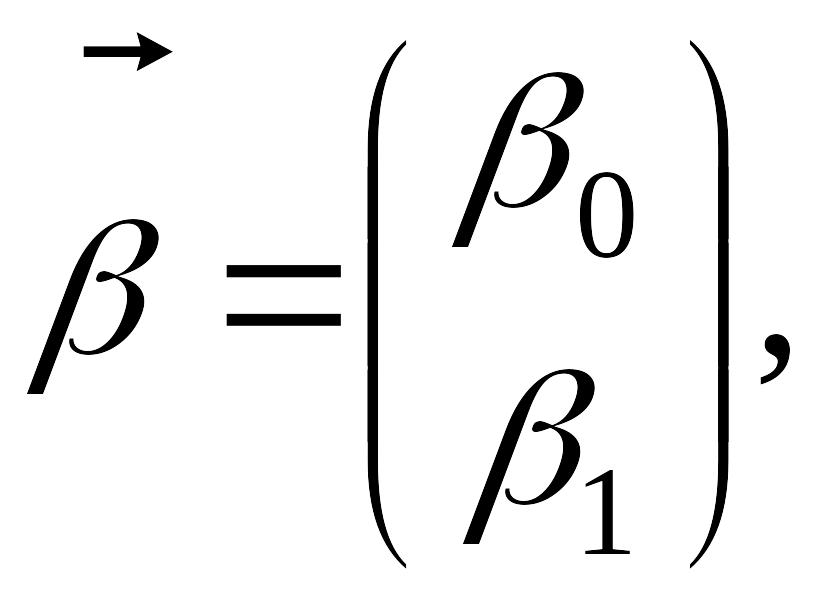
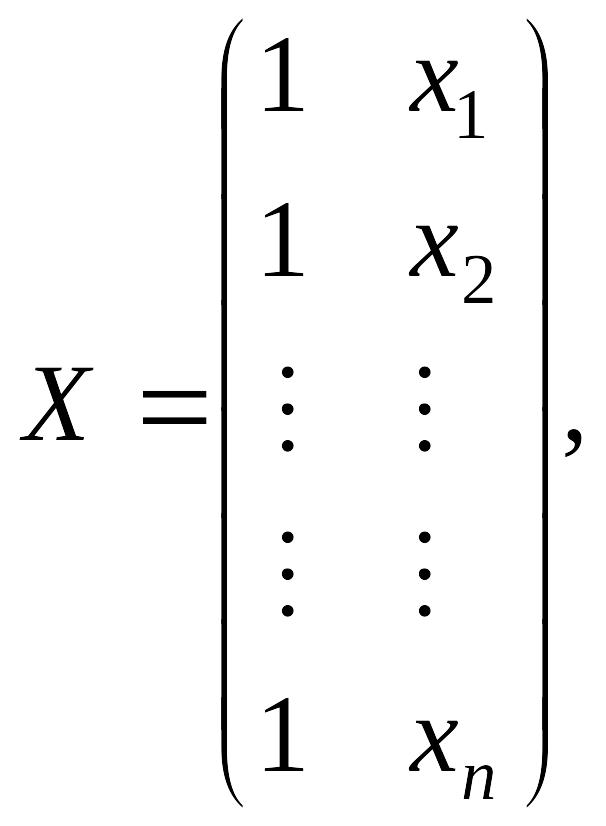
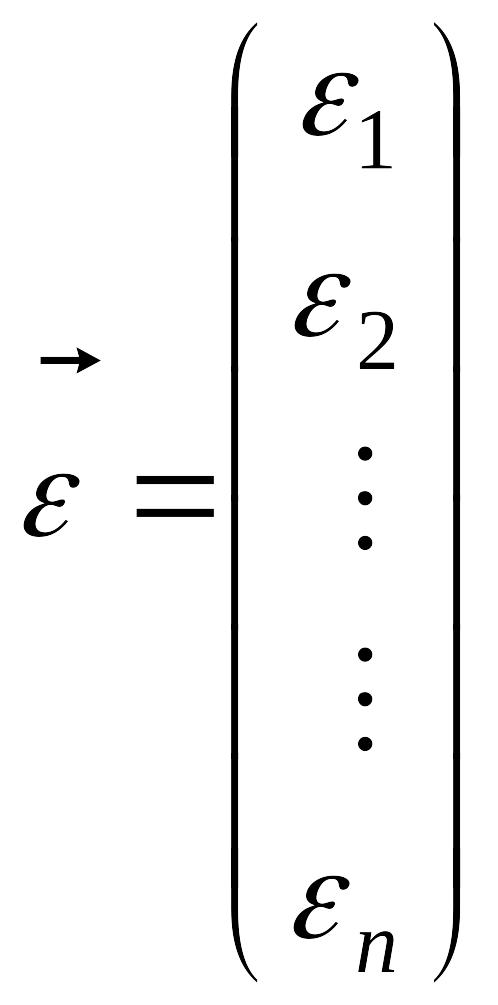
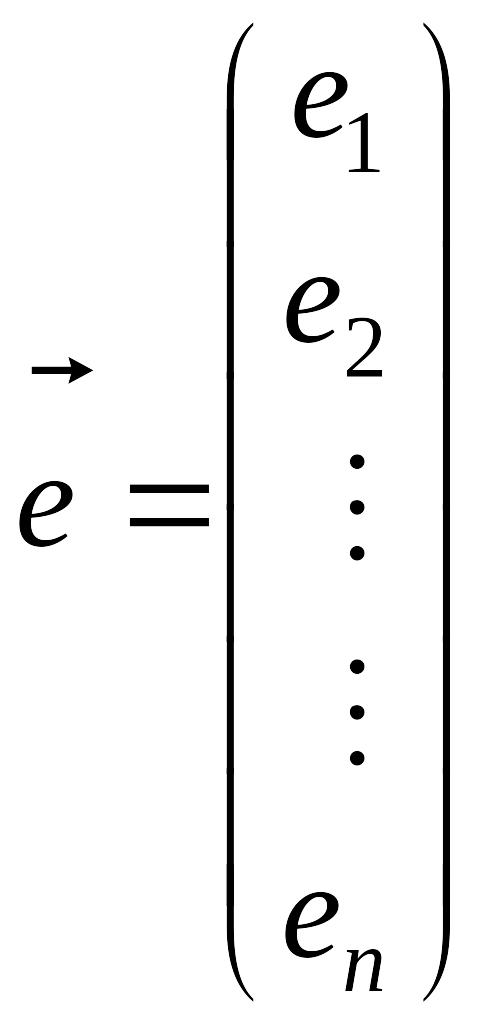