28.Автокоррреляционная функция случайной величины

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автокорреляционная функция (АКФ, ACF).

В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:

и показывает связь сигнала (функцииf(t)) с копией самого себя, смещённого на величину .

В теории случайных функций АКФ является корреляционным моментом двух значений одной случайной функции

Здесь , - Математическое ожидание!!!

используем формулу из книги Малышенко:

Автокорреляционная функция является важной статистической

характеристикой случайной функции, характеризующая взаимообуслов-

ленность значений последней в моменты времени t1 и t 2 . Если

вычислить её значения при различных моментах времени t1 и t 2 , то

получим полную характеристику такой зависимости.

График автокорреляционной функции можно получить, отложив по оси ординат коэффициент корреляции двух функций (базовой и функции сдвинутой на величину ) а по оси абсцисс величину . Если исходная функция строго периодическая, то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности базовой функции, а следовательно, и о её частотных характеристиках. Это применяется для анализа сложных колебаний, например электроэнцефалограммы человека.

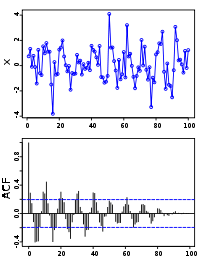
График 100 случайных величин со скрытой синусоидой. Автокорреляционная функция позволяет увидеть периодичность в ряде данных.

ПРИМЕНЯЕТСЯ ДЛЯ МЕСТА УТЕЧКИ В ТРУБОПРОВОДЕ.

Секрет от Рудницкого: Мат. ожидание и дисперсия в Автокорреляционной-функции автоматизированы:

1) X(t), t

2)

3) (t)=x(t)

4) (T) задержка

или ( ) и (

5) multiplication

6) Делим на 2т

29. Взаимная корреляционная функция двух случайных сигналов.

Для начала введем понятие корреляционная функция.

Корреляция - статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). А корреляционная функция — функция времени или пространственных координат, которая задает корреляцию в системах со случайными процессами.

Зависящая от времени корреляция двух случайных функций X(t) и Y(t) определяется как:

где угловые скобки обозначают процедуру усреднения.

Взаимнокорреляционная функция — стандартный метод оценки степени корреляции двух последовательностей. Она часто используется для поиска в длинной последовательности более короткой заранее известной. Рассмотрим два ряда f и g. Взаимная корреляция определяется по формуле:

где i — сдвиг между последовательностями относительно друг друга, а верхний индекс в виде звёздочки означает комплексное сопряжение. В общем случае, для непрерывных функций f (t) и g (t) взаимная корреляция определяется как

Если Х и У — два независимых случайных числа с функциями распределения вероятностей соответственно f и g, тогда взаимная корреляция f g соответствует распределению вероятностей выражения -Х+У . Напротив, свёртка f g соответствует распределению вероятностей суммы Х+У .

Корреляционные функции позволяют характеризовать вход-выходные взаимосвязи в системах при случайных воздействиях и широко используются на практике.

Либо можно так.

Для двух взаимосвязанных случайных функций x(t) и y(t) можно ввести понятие двухмерной плотности вероятности w(x, ; y, ), аналогичное по смыслу ранее введенной двухмерной плотности вероятности w( , ; , ). Тогда момент второго порядка вида:

будет называться взаимной корреляционной функцией случайных процессов x(t), y(t) . Он характеризует их взаимообусловленность в моменты, соответственно, и . Такие корреляционные функции позволяют характеризовать вход-выходные взаимосвязи в системах при случайных воздействиях и широко используются на практике.