6 Детерминированные и случайные переменные описывающие системы

Математическое описание состояний, процессов, свойств, характеристик систем сводится к составлению характеризующих их равенств, неравенств и/или функций. Константы этих функций, равенств и неравенств образуют множество постоянных параметров описываемых систем. Переменными у систем могут быть величины, которые характеризуют их входные воздействия;

• параметрическое, координатное, структурное и/или алгоритмическое состояние;

• динамику протекающих в них процессов;

• также те величины, которые отражают описываемые свойства или характеристики.

С позиции системного анализа переменные могут быть разбиты на две группы:

1. Независимые переменные─ часть изменяющих свое значение величин, которые изменяются под действием внешней для данной системы среды.

2. Зависимые переменные ─ тепеременные которые изменяются под действием независимых переменных.

Переменные могут быть вещественными, целочисленными, комплексными и/или логическими. Переменная каждого из этих типов может быть как детерминированной, так и случайной, а изменение во времени может быть либо непрерывным, либо дискретным.

Детерминированными переменными понято называть такие величины, которые могут изменять свои значения (в том числе во времени).

7. Основные способы математического описания детерменированных переменных.

Математическое описание детерминированных непрерывных переменных, используемое в теории систем, в том числе и в технической кибернетике, сводится к установлению их аналитических зависимостей от времени, их операторных изображений или спектральных составов.

Для независимых детерминированных переменных исследуемых или синтезируемых систем их аналитические зависимости выбираются в соответствии с их реальными изменениями в системе или исходя из интересующих разработчиков или исследователей влияний внешней среды на эти системы. Довольно часто при этом внешние воздействия на систему x(t) принимаются изменяющимися скачкообразно по уровню, т.е. в виде:

где единичная функция

Другими типовыми воздействиями на систему, часто используемыми при анализе или синтезе систем являются:

1) гармонические воздействия вида

2) воздействия, нарастающие с течением времени.

3) воздействия импульсного типа, форма которых может изменяться в зависимости от типа исследуемой системы. Часто таковым выбирается импульс, соответствующий дельта-функции Дирака равной нулю всюду при и бесконечности при , причем

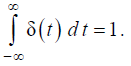
Эта функция технически не реализуема в виде сигнала, но удобна в исследованиях систем, т.к. достаточно просто связана с рядом важных типовых характеристик динамических систем (см. главу 8).

Экспериментальные данные, полученные при анализе систем, часто представляют в аналитической форме, используя для этого так называемые сплайны-функции времени вида:

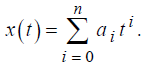
Наиболее часто при этом используются сплайны второго и третьего порядка (когда n равняется 2 или 3). Сплайны широко используются также при задании программ работы автоматических систем и отражают при этом требуемые изменения во времени программно изменяемых величин.

Другой, широко используемой в инженерной практике и научных исследованиях формой представления переменных – функций времени, является их разложение по той или иной системе ортогональных функций. Такие разложения дают вполне адекватное описание функций x(t) достаточно общего вида при конечном числе членов разложения . Кроме того, оно позволяет в дальнейшем сравнительно просто проводить необходимые математические преобразования членов подобного разложения.

Введем необходимые для дальнейшего изложения определения. Две функции определенные на интервале (2.3), называются ортогональными на этом интервале, если они удовлетворяют условию:

(2.4)

Система функций , определенных на интервале, называется ортогональной системой функций, если все эти функции попарно ортогональны, т.е. удовлетворяют условию. При этом обычно полагают, что

В тех случаях, когда , ортогональная система функций называется нормальной. Совокупность таких функций называют также сокращенно ортонормальной. Если же это условие не выполнено, то при желании всегда исходную систему ортогональных функций можно привести к нормальной, выбрав в качестве последней совокупность функций вида:

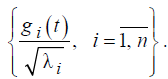
К числу ортогональных систем функций относится, например, тригонометрический ряд:

1, sin t, cos t, sin 2t, cos 2t, sin 3t, cos 3t, … , sin nt, cosnt, …

Различают счетные и континуальные наборы ортогональных функций. Счетными они называются в тех случаях, когда удовлетворяют условию (2.4).

Континуальные наборы ортогональных функций удовлетворяют условию:

Произвольную непрерывную или кусочно-непрерывную на интервале 2.3. функцию x(t) можно разложить в ряд по полному набору ортонормальных функций, т.е. представить в виде обобщенного ряда Фурье [1,9,15,17]:

Счетные наборы ортонормальных функций обладают рядом важных в практическом плане свойств. В частности, выбор коэффициентов c_i согласно (2.6) при аппроксимации x(t) рядом (2.5) обеспечивает минимум среднеквадратической ошибки такой аппроксимации по сравнению с любой другой взвешенной суммой ортонормированных функций. К тому же увеличение числа членов ряда (2.5) не влечет за собой изменения коэффициентов c_iранее использовавшегося ряда. В этой связи при подобном увеличении числа элементов ряда (2.5) не требуется производить перерасчет этих коэффициентов, что удобно при практическои использовании этого ряда. Существенным является и тот факт, что при x(t), удовлетворяющем условию

коэффициенты c_i0 при iбесконечности.

При аппроксимации функций конечным рядом (2.5) имеется возможность введением весовой функции w(t) изменять вклад в среднеквадратическую ошибку

такой аппроксимации отдельных ортогональных функций g_i(t). Для этого вместо условия ортогональности (2.4) следует применить условие

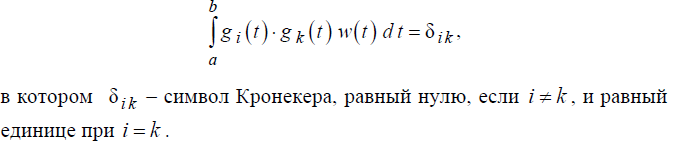
Наиболее часто используемые на практике наборы ортогональных функций приведены в приложении 1. Там же указаны и использумые при их определении интервалы [a,b] и значения весовых функций w(t).