Неравенство Крафта
Теорема. Неравенство Крафта.
Пусть 
- число символов алфавита кодировки и
задано множество целых положительных
чисел
, тогда неравенство
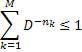
является необходимым и достаточным
условием существования множества
кодовых слов, соответствующих концевым
узлам кодового дерева, с длинами 
.
Доказательство.
Необходимость.
Допустим удалось построить дерево с
концевыми узлами порядка 
.
Узлов максимального порядка может быть
Это число достигается тогда, когда из
каждого промежуточного узла исходит
ровно 
Но в кодовом дереве существуют узлы
порядка 
не больше 
,
но такой концевой узел исключает 
узлов максимального порядка.
Достаточность.
Пусть справедливо
Докажем, что мы можем построить кодовое дерево.
Упорядочим все узлы в порядке возрастания
и предположим, что удалось построить
часть кодового дерева, которая включает
в себя узлы порядка 
-
некоторое число
Предположим, что кодовое дерево содержит
узлов порядка m. Если так
и справедливо неравенство
то:
т.е. все эти узлы порядка 
могут быть размещены в дереве – для них
найдется место.
Произвольный выбор 
– свидетельствует о том, что кодовое
дерево может быть построено.