• число позиций – 2;

• Число полков у полковника Блотто – 4;

• число полков у противника – 3.

Правила определения платежей:

• если на позиции у полковника полков больше, чем у противника, то он получает все полки противника и плюс один полк, так как занятие позиции эквивалентно захвату одного полка;

• если на данной позиции у полковника полков меньше, то он теряет свои полки на данной позиции и плюс позицию, то есть еще один полк;

• общий платеж равен сумме платежей на обеих позициях.

У полковника Блотто есть пять стратегий, у противника – четыре стратегии по распределению полков на двух позициях. Распределение платежей в зависимости от выбранной стратегии заносится в платежную матрицу

		b1	b2	b3	b4
		3,0	0,3	2,1	1,2
a1	4,0	4,0	1,–1	3,–1	2,–1
a2	0,4	–1,1	0,4	–1,2	–1,3
a3	3,1	0,1	1,–2	3,0	2,–2
a4	1,3	–2,1	1,0	–2,2	0,3
a5	2,2	–3,1	1,–3	0,2	2,0

Суммарная платежная матрица имеет вид:

min выигрыш А		b1	b2	b3	b4
		3,0	0,3	2,1	1,2
a1	4,0	4	0	2	1	0
a2	0,4	0	4	1	2	0
a3	3,1	1	–1	3	0	–1
a4	1,3	–1	1	0	3	–1
a5	2,2	–2	–2	2	2	–2
max проигрыш В		4	4	3	3

Оптимальный выбор стратегии для А – наибольший из минимальных выигрышей – max из min – 0, 0 (a₁, a₂).

Оптимальный выбор стратегии для В – наименьший из максимальных проигрышей – min из max – 3, 3 (b₃, b₄).

Обычно при выборе стратегии руководствуются одним из принципов: осторожности (минимакса) Гурвица или Сэвиджа.

Математические модели теории игр с полной информацией. Принцип осторожности

Модель игры может быть представлена в матричной форме в виде суммарной платежной матрицы

Наименьший выигрыш А_i

	B1	B2	B3	B4
А max min 1	35	35	3	10	3
А2	24	1	6	90	1
А3	40	60	10	15	10
Наибольший проигрыш Вj	40	60	10	90

min max

Сторона А имеет три стратегии (А₁, А₂, А₃). Сторона В – четыре стратегии (В₁, В₂, В₃, В₄).

Получаем две границы игры:

a – max min c_ij = 10 – максимальный выигрыш

j i

b – min max c_ij = 10 – минимальный проигрыш

i j

a – нижняя цена игры;

b – верхняя цена игры;

a = b – решение находится в области чистых стратегий;

a ≠ b – стратегии смешанные;

c₃₃ – седловая точка (отклонение уменьшает выигрыш).

Если стратегии известны, то они называются числовыми стратегиями.

Суть принципа:

Если стратегия В не известна для А, то А выбирает стратегию, обеспечивающую из минимально возможных выигрышей максимальное значение.

Если стратегия А не известна для В, то В применяет стратегию, обеспечивающую минимальный из максимально возможных проигрышей.

Если А стала известна стратегия В, то А выбирает ту стратегию, которая приведет В к максимальному проигрышу.

Если В известна стратегия А, то В выбирает стратегию, обеспечивающую минимальный выигрыш А.

Математические модели теории игр с неполной информацией

Если седловой точки нет, то для А стратегии смешанные. Выбор стратегии ограничен с вероятностями или частотами при многократной игре:

; ,

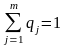где p_i, q_i - вероятности применения стратегий А и В.