22.. Оценка динамических погрешностей при использовании аналоговых средств измерения

Простейшая оценка динамических погрешностей при исполь­зовании аналоговых средств регистрации. Как видно из данных табл. 1-1, с применением ручной записи показаний, цифропе-чати или перфораторов могут быть зарегистрированы только очень медленные процессы с периодом 0,6 с — 2,2 мин (при у_т «s яй 1%). Поэтому для регистрации процессов, протекающих с ча­стотами от 1 Гц до 5—50 кГц, широко используются аналоговые средства регистрации: самопишущие приборы с чернильной за

СО, 1

° 4

f f f

^тгр 'rp ^lo

Рис. 1-8

писью, светолучевые и электронные осциллографы с фотопри- . ставками.

Динамические погрешности таких приборов, а также исполь-вуемых в комплекте с ними датчиков и усилителей принято нор­мировать указанием их амплитудно-частотной характеристики, представляющей собой график зависимости от частоты / отноше­ния их чувствительности 5 при частоте / к чувствительности 5 при / = О (см. ГОСТ 8.256—77).

В большинстве случаев эти характеристики имеют вид кривых, показанных на рис. 1-8. При апериодической частотной характе­ристике (рис. 1-8, а) (показывающие приборы, усилители, дат­чики температуры и т. п.) чувствительность 5 прибора или дат­чика монотонно понижается с ростом частоты / воспринимаемого процесса. Частотная погрешность y_f есть разность между орди­натами частотной характеристики и постоянным уровнем S/S₀ = s= 1, показанным на рис. 1-8, а штриховой прямой. Она всегда отрицательна и увеличивается с ростом частоты /. Ее численное значение может быть найдено из этого графика для лю­бой частоты и использовано для оценки точности регистрации или введения поправки в результат измерения.

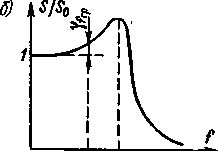
Частотная характеристика, изображенная на рис. 1-8, б, ха­рактерна для колебательных систем с малым успокоением (галь­ванометров, светолучевых осциллографов, датчиков манометров, акселерометров и т. д.). Она имеет резонансный пик вблизи соб­ственной частоты /о колебательной системы иположитель-н у ю частотную погрешность y_f.

Для приборов и датчиков с такими частотными характеристи­ками нормируется рабочий диапазон частот, простирающийся от / = 0 до такой частоты /_гр, где y_f достигает некоторого гранич­ного значения ^/гр- Так как граничное значение частотной по­грешности достигается только в конце рабочего диапазона частот, то внутри его частотные погрешности оказываются много меньше этого значения.

Располагая частотной характеристикой прибора или датчика, можно найти частотную погрешность для любого значения ча­стоты регистрируемого процесса внутри рабочего диапазона ча­стот. Так, например, при частотной характеристике, приведенной

на рис. 1-8, б, частотная погрешность может быть рассчитана по

формуле

?, » (1 - 2р^а) (Ш^а, (1-Ю)

где р ■— степень успокоения колебательной системы; fa — ее собственная частота.

При отсутствии успокоения ф ж 0), что характерно для дат­чиков, не имеющих специальных средств успокоения, частотная погрешность

?/«(Ш^а. 0-И)

Так же легко может быть вычислена частотная погрешность и для апериодических (неколебательных) преобразователей не­высоких порядков. Так, например, термопара или термометр сопротивления могут быть представлены апериодическим звеном первого порядка (с одной постоянной времени). Для них частотная погрешность может быть приближенно выражена как

?**-4-<ш\ (М2)

где f_c ■== (2ПТ)"¹ — так называемая частота среза частотной ха­рактеристики, а т — постоянная времени.

Практическое использование формул (1-11) и (1-12) рассмо­трим на двух конкретных примерах.

Пусть для регистрации пульсирующего давления исполь-вуется мембранный датчик (тензометрический, пьезоэлектриче­ский, емкостный или индуктивный) с собственной частотой /₀ =а t= 5 кГц. Какие процессы и с какой погрешностью могут быть им измерены? Полагая, что степень успокоения датчика |3 ?» 0, и используя соотношение (1-11), получаем, что при частоте измеряе­мого процесса / = 50 Гц его частотная погрешность y_f = 0,01 %, но при / в= 100 Гц уже «р/ = 0,04%, при / = 500 Гц -р/ =1%, а при / = 1000 Гц 7/ =4%, т. е. рабочий диапазон частот дат­чика оказывается уже исчерпанным.

Пусть периодические колебания температуры измеряются с помощью термопары или термометра сопротивления средней инерционности с постоянной времени чг == 1 мин = 60 с. Спраши­вается, каков рабочий диапазон частот такого датчика? Для этого преобразуем формулу (1-12), заменив / на 1/Т, где Т — период измеряемого процесса; тогда получим

„ 1 f* __ 1 (2ят)^а 2я^ат^а

Т/ ^ 2 /² 2 Т^% Т^%

Подставляя в это выражение разные вначения периода Т измеряемых колебаний, получим частотную погрешность <ру = = 0,14% при периоде колебаний Г =2 ч, ^/ =0,5% —при Т = 60 мин, ^ в 2% — при Т s= 30 мин, ^ = 5% —- при Т =

г— 20 мин, т. е. рабочий диапазон частот можно считать исчерпан­ным.

Соотношения (1-11) и (1-12) показывают, что частотная по­грешность возрастает пропорционально квадрату частоты, что, как и при дискретных отсчетах 1см. формулу (1-9)], приводит к очень неблагоприятным соотношениям при регистрации неси­нусоидальных процессов. Поэтому изложенные выше предосте­режения остаются актуальными и в этом случае.