18.. Расчет оценки статической погрешности результата измерения по паспортным данным используемого си.

Результат измерения имеет ценность лишь тогда, когда можно оценить его интервал неопределенности, т. е. степень достоверности. Поэтому согласно ГОСТ 8.011—72 «Показатели точности измерений и формы представления результатов измерений» сообщение о любом результате измерений обязательно должно сопровождаться указанием его погрешности.

Погрешность результата прямого однократного измерения зависит от многих факторов, но, в первую очередь, определяется, естественно, погрешностью используемых средств измерений. Поэтому в первом приближении погрешность результата измерения можно принять равной погрешности, которой в данной точке диапазона измерений характеризуется используемое средство измерений.

Так как погрешности средств измерений изменяются в диапазоне, то вычисление должно производиться по соответствующим формулам. Вычисляться должна как абсолютная, так и относительная погрешности результата измерения, так как первая из них нужна для округления результата и его правильной записи, а вторая — для однозначной сравнительной характеристики его точности.

Для разных характеристик нормирования погрешностей СИ эти вычисления производятся по-разному, поэтому рассмотрим три характерных случая.

1. Класс точности прибора указан в виде одного числа g_s заключенного в кружок. Тогда относительная погрешность результата (в процентах) g(х)=g_s, а абсолютная его погрешность D(х)=g_sх/100.

2. Класс точности прибора указан одним числом g₀ (без кружка). Тогда абсолютная погрешность результата измерения D(х)=g₀X_к, где Х_к — предел измерений, на котором оно производилось, а относительная погрешность измерения (в процентах) находится по формуле

                                     (6)

т. е. в этом случае при измерении, кроме отсчета измеряемой величины х, обязательно должен быть зафиксирован и предел измерений x_к, иначе впоследствии нельзя будет вычислить погрешность результата.

3. Класс точности прибора указан двумя числами в виде g_к/g_н. В этом случае удобнее вычислить относительную погрешность результата по формуле (5), а уже затем найти абсолютную погрешность как D(х)=g(х)х/100.

При использовании этих формул полезно помнить, что в формулы для определения g(х) значения g_s, g₀, g_н и g_кподставляются в процентах, поэтому и относительная погрешность результата измерения получается также в процентах.

Однако для вычисления абсолютной погрешности D(х) в единицах х значение g(х) (в процентах) необходимо разделить на 100.

3.4.2 Правила округления значений погрешности и результата измерения.

Рассчитывая значения погрешности по формулам (5) и (6), особенно при пользовании калькулятором, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчета являются нормируемые значения погрешности СИ, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна-две значащие цифры. При этом приходится учитывать следующее. Если полученное число начинается с цифр 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30—50%), что недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, т. е. указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности.

Исходя из этого, на практике установилось такое правило:

если полученное число начинается с цифры, равной или большей  , то в нем сохраняется лишь один знак; если же оно начинается с цифр, меньших 3, т. е. с цифр 1 и 2, то в нем сохраняют два знака. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5% указываются два знака, но в числах 0,5; 4; 6% указывается лишь один знак.

В итоге можно сформулировать три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.

1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, — если первая есть 3 и более.

2. Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.

3. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.

Пример. На вольтметре класса точности 2,5 с пределом измерений 300 В был получен отсчет измеряемого напряжения х =267,5 В.

Расчет погрешности удобнее вести в следующем порядке:

необходимо найти абсолютную погрешность, а затем — относительную. Абсолютная погрешность D(х) =g₀X_к/100; при g₀=2,5%  и Х_к =300 В это дает   В » 8 В; относительная   

Так как первая значащая цифра значения абсолютной погрешности (7,5 В) больше трех, то это значение должно быть округлено по обычным правилам округления до 8 В, но в значении относительной погрешности (2,81%) первая значащая цифра меньше 3, поэтому здесь должны быть сохранены в ответе два десятичных разряда и указано g(х) =2,8%. Полученное значение х=267,5 В должно быть округлено до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности, т. е. до целых единиц вольт.

Таким образом, в окончательном ответе должно быть сообщено: Измерение произведено с относительной погрешностью g(х)=2,8%. Измеренное напряжение х=(268±8) В или х=268 В ± 8 В.

При этом более наглядно указать пределы интервала неопределенности измеренной величины в виде х=260—276 В или 260 В <х< 276 В.

Наряду с изложенными правилами округления значений погрешностей результатов измерения, иногда применяются и другие, некоторые из них изложены в книге Рабинович С.Г. Погрешности измерений. – Л.:Энергия ,1978.

Динамическая погрешность. Выбор СИ по их быстродействию.

В общем случае динамическая погрешность в передаче сигнала x(t), являющегося функцией времени, определяется разностью между действительным выходным сигналом y(t) в динамическом режиме и выходным сигналом уст= Sx(t) в статическом режиме при отсутствии инерционных свойств СИ, т.е. Али y(t) - Sx(t) = y(t) - уст, B.29)

где S — чувствительность СИ.

Динамическая погрешность — разность между погрешностями СИ в динамическом режиме и его статической погрешностью.

Измерение называют динамическим (в динамическом режиме), если нельзя пренебречь изменением величины во времени. Например, измерение мгновенного значения переменного тока или напряжения. С другой стороны, СИ, как правило, обладают инерционностью и не могут мгновенно реагировать на изменение входного сигнала. Поэтому при измерении изменяющегося во времени сигнала x(t) всегда возникает составляющая погрешности, обусловленная инерционными (динамическими) свойствами СИ. Эти свойства выражают с помощью динамических характеристик, однозначно устанавливающих отклик СИ на изменение входного воздействия. В качестве таких характеристик использует передаточную функцию; комплексный коэффициент переда — амплитудно-частотную характеристику (АЧХ); комплексную Чувствительность—фазочастотную характеристику (ФЧХ); переходную функцию — реакцию на единичный скачок; импульсную (вербую) функцию — реакцию на единичный импульс [10; 30; 55]. Указанные характеристики взаимосвязаны, и по одной из них моЖно найти все остальные. Методы их экспериментального определения также широко освещены в литературе по автоматичекоМу регулированию. При решении задач динамических измерений необходимо подобрать аналитические выражения для аппроксимации найденных или заданных динамических характеристик; найти аналитические выражения (с помощью специальных функций; полигонов, рядов и др.) для входных и выходных сигналов; определить собственно динамические погрешности; найти входной сигнал (например, состояния ТС) по зафиксированному выходному — восстановление сигнала. В общем случае динамическая погрешность в передаче сигнала x(t), являющегося функцией времени, определяется разностью между действительным выходным сигналом y(t) в динамическом режиме и выходным сигналом уст= Sx(t) в статическом режиме при отсутствии инерционных свойств СИ, т.е. Али„ = X') - Sx(t) = y(t) - уст, B.29) где S — чувствительность СИ. Динамической погрешностью является не только погрешность, оцениваемая по формуле B.29), но, например, и погрешность при идеальной передаче формы сигнала, сдвинутого во времени по фазе на т: Aoth= y(t + т) - уп. Динамические погрешности могут быть определены только расчетно-экспериментальным путем. Эталонов и образцовых СИ в области динамических измерений нет. Учитывая, что СИ входит в измерительную цепь наряду с другими звеньями (датчиками, усилителями, преобразователями, трансформаторами и т.д.), каждый из которых тоже обладает своими динамическими свойствами, в целом следует говорить о некотором аналоге измерительной цепи — измерительном преобразователе (ИП) с известными (заданными) динамическими характеристиками. Для описания динамических свойств ИП необходимо задать такие параметры, которые позволили бы для любого входного сигнала x(f) определить выходной y(f) сигнал, а также решить обраТную задачу (восстановление входного сигнала, т.е. оценки технического состояния ТС) с учетом дестабилизирующих факторов (помехи, внешние влияния, неинформативные параметры и т. Я-)-

20.. Численная оценка динамической погрешности.

Оценка величины динамической погрешности является сравнительно сложным процессом. Проблема возникает потому, что динамическая погрешность зависит не только от динамической модели измерительного канала, но и от формы измеряемого сигнала.

Основными источниками динамической погрешности являются естественная инерционность физических процессов, протекающих в датчиках, процессы заряда входной емкости измерительного устройства, инерционность фильтров, использованных для устранения алиасного эффекта и подавления помех в измерительном канале.

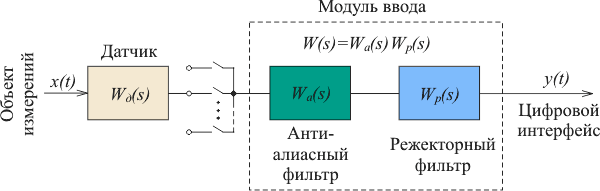
Рис. 4.9. Динамическая модель измерительного канала

Для количественного описания динамических свойств измерительного канала используют линейные динамические модели в виде дифференциальных уравнений, операторных передаточных функций, импульсных переходных характеристик или реакций на единичный скачок, амплитудно-частотные и амплитудно-фазовые характеристики (ГОСТ 8.256 [ГОСТ]). Описание этих моделей может быть указано в эксплуатационной документации на средство измерений. Идентификацию динамической модели средства измерений выполняет его разработчик, используя те же методы, что и при идентификации объекта управления (см. раздел "ПИД-регуляторы").

В некоторых случаях, например, когда уравнения динамической моделипользователю известны, могут быть заданы только коэффициенты уравнений, постоянные времени, время реакции (время установления), коэффициент демпфирования, полоса пропускания по уровню 0,707 и др.

Для модулей аналогового ввода может быть также задана погрешность положения отсчета измеряемого сигнала на оси времени.

Рассмотрим типовую динамическую модель измерительного канала (рис. 4.9), которая включает в себя модели датчика   и модуля ввода аналоговых сигналов  . Передаточная функция   обычно представляет собой произведение передаточных функций антиалиасного фильтра (стоящего до АЦП) и цифрового режекторного фильтра после АЦП. Измерительный преобразователь часто входит в состав модуля ввода.

При проектировании системы автоматизации динамические характеристики ее звеньев можно выбрать так, что инерционность всего измерительного канала будет определяться инерционностью самого медленного звена. Это существенно упрощает процесс оценки величины динамической погрешности. Например, при измерении температуры самым инерционным звеном должен быть датчик (инерционность термопар характеризуется постоянной времени десятки секунд и намного превышает инерционность модуля ввода (доли секунды)).

21.. Особенности измерения сложных несинусоидальных процессов.

Особенности измерения сложных иесииусоидальиых процессов.

На практике чаще всего приходится измерять существенно не­синусоидальные процессы, содержащие гармонические составляю­щие или высокочастотные составляющие шумов, помех или наво­док. В этих случаях динамическая погрешность восстановления процесса по дискретным отсчетам резко возрастает, о чем исследо­ватель должен всегда помнить.

Рассмотрим это свойство погрешности восстановления на кон­кретном примере. Так, в табл. 1-1 указано, что при использова­нии АЦП с периодом дискретизации t₀ =30 мкс исследуемый процесс g частотой f_x = 500 Гц восстанавливается с y_ml f& 0,1%. Действительно, рассчитывая у_тХ по формуле (1-9), получаем

Ъ*. = 4" #* = "Г" (30-10-⁶-500)² = 10"^s = 0,1 %,

что часто можно считать достаточно высокой точностью восстанов­ления. Однако если в кривой этого процесса содержится дополни­тельно еще 10-я гармоника с частотой /₁₀ = 5000 Гц и амплитудой в 0,1 основной волны, она будет восстанавливаться с относитель­ной погрешностью Ymio» ^в ЮО раз большей, чем у_т1, т. е. равной 10%. Правда, так как амплитуда этой гармоники в 10 раз меньше амплитуды основной волны, то приведенное значение этой погреш­ности составит лишь у_т10 = 1 %. Тем не менее результирующая погрешность восстановления всего процесса будет в 10 раз (!) больше, чем погрешность восстановления у_т1 =0,1% процесса, не содержащего этой высокочастотной составляющей.

Погрешность восстановления для основной волны и ее гармо­ник является систематической (она всегда отрицательна, см. рис. 1-7, и приводит к уменьшению восстанавливаемой амплитуды кривой), однако если высокочастотная составляющая вызвана шумом или другими помехами и не синхронна с основной волной, то и погрешность восстановления оказывается случайной и наб­людается в виде случайного разброса отсчетов.

При ручной регистрации наблюдений подобный разброс дан­ных будет сразу замечен экспериментатором и он примет соответ­ствующее решение о ходе эксперимента. Рассмотренное явление особенно опасно при автоматическом вводе данных в ЭВМ и под­черкивает крайнюю важность метрологического анализа динами­ческих погрешностей в этом случае.