44.. Методы обработки и оценки погрешностей при однофакторном эксперименте.

МЕТОДЫ ОБРАБОТКИ И ОЦЕНКИ ПОГРЕШНОСТЕЙ |ПРИ ОДНОФАКТОРНОМ ЭКСПЕРИМЕНТЕ

I.

Ь-Ь ЦЕЛЬ И ОСОБЕННОСТИ ЭКСПЕРИМЕНТА

ПО ОПРЕДЕЛЕНИЮ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ

1

На практике сама необходимость измерений большинства величин вызывается именно тем, что они не остаются постоянными, а изменяются в функции от изменения, других величин. В этом случае целью измерения является, установление вида функци­ональной зависимости у —f(x). Для. этого должны одновременно определяться как значения .ж, так и соответствующие им значе­ния у, а задачей эксперимента является, как принято теперь говорить, установление математической модели исследуемой за­висимости.

Определение математической модели включает в себя указание вида модели и определение значений ее параметров (коэффициентов, показателей степени и т. д.). Искомая функция может быть как функцией одной независимой переменной, так и функцией многих переменных. В современной теории экспери­мента независимые переменные принято называть факторами,. а зависимую переменную у — откликом (ГОСТ 24026—80). В соот­ветствии с этим стандартом эксперимент по определению функции вида у ~f (х) принято именовать однофожторным, а эксперимент по определению функций вида у = F (х_ъ ..., x_k) — многофактор­ным. В дальнейшем будем использовать терминологию ГОСТ 24026—80, а не ГОСТ 16263—70, подразделяющего такие измерения, на совместные и совокупные. Вопросы, относящиеся к однофакторному эксперименту, будут рассмотрены в данной главе, а обработке и оценке погрешностей многофакторного экс­перимента будет посвящена гл. 7.

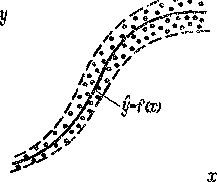
Искомая, математическая модель функциональной зависимости S ~f(x) может быть найдена лишь в результате совместной обработки всех полученных значений х ___„

к у. На рис. 6-1 это кривая, проходя­ щая по центру полосы эксперименталь­ ных точек, которые могут и не лежать на искомой кривой § = / (х), а зани­ мают некоторую полосу вокруг нее. Эти отклонения вызваны погрешно­ стями измерений, неполнотой модели ^и учитываемых факторов, случайным характером самих исследуемых процес­ сов и другими причинами. Разделить кярешноега,, вызванные неточностьюРис. 6-1

измерения х и неточностью измерения, у, невозможно, так как смещение точки на рис. 6-1, например, выше кривой могло быть вызвано как положительной погрешностью при измерении у, так и отрицательной погрешностью при измерении х. Поэтому описанием погрешности исходных данных может быть лишь указание ширины полосы их разброса вокруг найденной кривой зависимости & = f (х). При этом полоса разброса экспери­ментальных данных необязательно будет иметь постоянную ширину по всей своей длине. Она может быть узкой вначале и расширяться, в конце или, например, иметь узкий перешеек в средней части и расширяться по концам и т. п. Поэтому форма полосы погрешностей должна анализироваться в каждом отдель­ном случае.

45.. Оценка коэффициента корреляции и погрешности исходных данных при однофакторном эксперименте.

Быстрая оценка коэффициента корреляции и погрешности исходных данных также может быть произведена методом медиан­ных центров. Для этого обведенное прямоугольным контуром поле исходных данных (рис. 6-3, в) вначале разбивается вертикальной границей на две равные по числу точек области, в каждой из ко­торых находятся медианные центры, отмеченные на рисунке кре­стиками. Через них проводится прямая 1, являющаяся линией регрессии у по х.

Затем поле точек разбивается горизонтальной границей на две части с равным числом точек, и в каждой из них также находятся медианные центры, помеченные на рисунке незалитыми точками. Через эти центры проводится прямая 2, являющаяся линией регрессии х по у. (Эти понятия рассматриваются в пояснении рис. 6-10.)

Прямые 1 и 2 совпадают между собой и с прямой 3 лишь при коэффициенте корреляции между х и у р_жг, = 1, когда все экспе­риментальные точки лежат строго на прямой 3, т. е. погрешность разброса исходных данных <у = 0. При у^О ир^1 прямая 1идет положе прямой 3 на величину коэффициента корреляции р, а прямая 2 — во столько же раз круче. Поэтому если прямая 1 имеет уравнение у = а_х + Ь_хх, а прямая 2 — уравнение у =» с== й₂ + Ь_гх, то всегда 6₂ > W и р = Vbjb_u, а относительная (приведенная к диапазону изменения у) погрешность исходных данных, как было отмечено в § 3-1, будет >р = 1/(1 — р^а)/4.

46.. Методы установления графического вида однофакторных зависимостей.

Быстрые методы установления графического вида однофак-торных зависимостей. Основной помехой для установления, вида исследуемой зависимости является случайный разброс экспери­ментальных данных.

Если случайный разброс координат х и у почти отсутствует или, как иногда говорят, диффузность исходных данных очень мала, то привлечение статистических методов для. их обработки излишне и кривую можно просто провести через эти точки. Однако даже в этом случае не следует соединять нанесенные на график экспериментальные точки отрезками прямых линий, а провести через них плавную кривую. При проведении такой кривой (рис. 6-2, с) может оказаться, что одна или две точки все-таки не лежат на этой кривой и их следует рассматривать как возмож­ные выбросы или промахи.

Если диффузность исходных данных значительна, т. е. вслед­ствие случайного разброса отсчетов х и у точки на графике имеют существенный случайный разброс, то соединение их между собой отрезками прямых линий (рис. 6-2, б) просто бессмысленно и для обработки таких данных надо применять простейшие или более сложные статистические методы.

Одним из таких простейших экспресс-мегодов статистической обработки является метод обведения, контура плавных границ полосы рассеяния экспериментальных точек. Если при этом для. сохранения плавности этих границ какие-то из точек приходится оставить вне контура (рис. 6-2, в), то их следует рас­сматривать как возможные промахи или аномально большие слу­чайные отклонения. Форма обведенной контуром полосы рассея­ния экспериментальных точек чаще всего уже позволяет вынести суждение о характере функциональной зависимости у = f (х). Для однозначного указания, вида этой зависимости необходимо провести на глаз осевую линию этого контура.

Несмотря, на исключительную простоту метода контура, он позволяет быстро указать желаемое положение и форму искомой кривой и провести ее не через какие-то отдельные точки, а сообра-^вУясь с положением на графике всех экспериментальных точек ^в Целом. Однако при большом рассеянии результатов экспери­мента форма контура может иметь бессмысленные, случайные очертания. В этих условиях приходится, ограничиваться, уста­новлением лишь уровня и наклона искомой вависимости, полагая

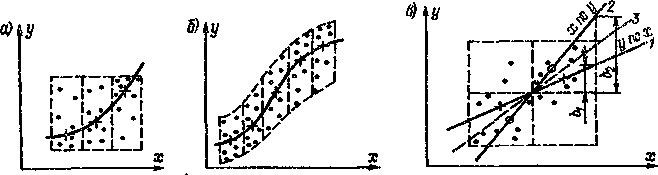
Рис. 6-3

ее прямой линией (рис. 6-2, г), проходящей по центру обведенной контуром полосы точек.

При очень большой диффузности экспериментальных данных, когда использование метода контура не, дает ответа, может ока­заться полезным метод медианных центров. Сущность этого ме­тода поясняет рис. 6-3, а. Обведенное контуром поле точек делят на несколько частей, и в каждой из них находят медианный центр, т. е. пересечение вертикали и горизонтали слева и справа, и выше и ниже которых оказывается равное число точек. Затем через эти медианные центры проводят плавную кривую. Так как общее число отсчетов, как правило, не очень велико, то не следует стремиться к разделению поля точек на излишне большое число областей. Так, например, если поле точек на рис. 6-2, г решено описать прямой линией, для определения положения которой достаточно двух медианных центров, то и поле точек нужно раз­делить только на две равноценные области. Положение и форма кривых на рис. 6-3, а и б определяется соответственно тремя и пятью точками. Поэтому и поля точек должны быть разбиты не бо­лее чем на три и пять областей.

Быстрая оценка коэффициента корреляции и погрешности исходных данных также может быть произведена методом медиан­ных центров. Для этого обведенное прямоугольным контуром поле исходных данных (рис. 6-3, в) вначале разбивается вертикальной границей на две равные по числу точек области, в каждой из ко­торых находятся медианные центры, отмеченные на рисунке кре­стиками. Через них проводится прямая 1, являющаяся линией регрессии у по х.

Затем поле точек разбивается горизонтальной границей на две части с равным числом точек, и в каждой из них также находятся медианные центры, помеченные на рисунке незалитыми точками. Через эти центры проводится прямая 2, являющаяся линией регрессии х по у. (Эти понятия рассматриваются в пояснении рис. 6-10.)