
- •5.. Метрология. Метод, принцип, средство измерения. Понятие точности и истинного значения.
- •6.. Методы измерений. Понятие меры.
- •7.. Виды и методы измерений
- •8.. Организация измерительного дела в стране. Эталоны. Система передачи единиц
- •14.. Понятия полосы погрешностей, реальной и номинальной характеристик средств измерений
- •15.. Абсолютная, относительная и приведенная погрешность си. Аддитивные и мультипликативные погрешности. Погрешности квантования.
- •16.. Методы нормирования погрешностей средств измерения.
- •18.. Расчет оценки статической погрешности результата измерения по паспортным данным используемого си.
- •3.4.2 Правила округления значений погрешности и результата измерения.
- •22.. Оценка динамических погрешностей при использовании аналоговых средств измерения
- •23.. Изменение погрешности си во время их эксплуатации.
- •24.. Методы вероятностного описания погрешностей средств и результатов измерений
- •28.. Вероятностные оценки ширины распределения. Предельная и квантильная оценка
- •29.. Достоверность определения доверительного значения погрешности по экспериментальным данным
- •30. Методы расчетного суммирования составляющих результирующей погрешности. Дисперсия
- •32. Практические правила расчетного суммирования составляющих результирующей погрешности и квантильного коэффициента.
- •33. Расчет погрешности результатов косвенных измерений.
- •35.. Методы уст ранения постоянных систематических погрешностей.
- •7.6. Частотные характеристики апериодического сигнала
- •44.. Методы обработки и оценки погрешностей при однофакторном эксперименте.
- •45.. Оценка коэффициента корреляции и погрешности исходных данных при однофакторном эксперименте.
- •47.. Расчет по экспериментальным данным параметров выбранной аппроксимирующей функции.
- •3 Группы для измерения температуры:
35.. Методы уст ранения постоянных систематических погрешностей.
Методы исключения систематических погрешностей
В теоретической метрологии принято считать, что систематические погрешности можно обнаружить и исключить из результата измерения. Однако в реальных условиях полностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то не исключенные факторы, которые нужно учитывать и которые будут вызывать систематическую погрешность измерения. Это значит, что систематическая погрешность тоже случайна и ее определение обусловлено лишь установившимися традициями обработки и представления результатов измерения. Для результата измерения не обнаруженная систематическая составляющая погрешности гораздо опаснее случайной погрешности: если случайная составляющая вызывает вариацию (разброс) результатов, то систематическая — устойчиво их искажает (смещает результаты измерений, содержащие систематическую погрешность, относятся к неисправленным. В любом случае отсутствие или незначительность (пренебрежение) систематической погрешности надо доказать. Постоянные систематические погрешности можно обнаружить только путем сравнения результатов измерений с другими, подученными с использованием более точных методов и средств измерения. В ряде случаев систематическую погрешность можно исключить путем устранения источников погрешности до начала измерений (профилактика погрешности), а в процессе измерений — внесением известных поправок в результаты измерений. Профилактика — наиболее рациональный способ снижения погрешности, который заключается в устранении влияния, например, температуры (термостатированием и термоизоляцией), магнитных полей (магнитными экранами), вибраций и т. п. Сюда же относятся регулировка, ремонт и поверка средств измерений.
Метод замещения обеспечивает наиболее полную компенсацию постоянной систематической погрешности. Суть данного метода состоит в такой замене измеряемой величины хи известной величиной Δ, получаемой с помощью регулируемой меры, чтобы показание измерительного прибора сохранилось неизменным. Значение измеряемой величины считывают в этом случае по указателю меры. При использовании данного метода погрешность неточного измерительного прибора устраняют, а погрешность измерения определяют только погрешностью самой меры и погрешностью отсчета измеряемой величины по указателю меры.
Пример 4.2. Омметром малой точности измерялось сопротивление резистора Rx. Результат измерения равен х = Rx + Δс, где х и Δс — соответственно показание омметра и систематическая погрешность измерения. Решение. Заменив Rxмагазином сопротивлений и отрегулировав его так, чтобы сохранилось показание омметра, получимх = RM + Δс. Из двух приведенных выражений для х следует, что Rx = Rм. Метод компенсации погрешности по знаку используют для устранения постоянной систематической погрешности, у которой в зависимости от условий измерения изменяется только знак. При этом методе выполняют два измерения, результаты которых соответственно есть х1 = хu + Δс и х2 = хи - Δс, где хu— измеряемая величина Среднее значение из полученных результатов
(х1 + х2)/2 = хu представляет собой окончательный результат измерения, не содержащий погрешности ± Δс. Данный метод наиболее часто применяют при измерении экстремальных значений (максимума и нуля) неизвестной физической величины.
Пример 4.3. Показания вольтметра подвержены влиянию магнитного поля Земли. В результате возникает погрешность измерения ΔU.
Решение. Произведя два измерения напряжения при противоположной ориентации прибора относительно меридиана, получим U1 = Ux + ΔU и U2 = UX- ΔU.Отсюда напряжение Ux= (U1 + U2)/2. Метод введения поправок позволяет достаточно просто вычислить и исключить из результата измерения систематические погрешности. Напомним, что поправка С — величина, одноименная с измеряемой хu, вводимая в результат измерения х = хu+ Δс + С с целью исключения систематической погрешности. В случае принимают С = - Δс и систематическая погрешность полностью исключается из результата измерения. Поправки определяют экспериментально или путем специальных теоретических исследований и задают в виде формул, графиков или таблиц.
Пример 4.4. Показания вольтметра при измерении напряжения в сети переменного тока составили 219В.
Решение. В свидетельстве о поверке данного прибора указано, что на этой отметке его шкалы систематическая погрешность вольтметра составляет Δс = - 1 В. С учетом поправки напряжение в сети 219 + 1 = 220 В. Ввод одной поправки позволяет исключить влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить несколько поправок.
Метод противопоставления применяется в радиоизмерениях для уменьшения постоянных систематических погрешностей при сравнении измеряемой величины с известной величиной примерно равного значения, воспроизводимой соответствующей образцовой мерой.
Данный метод является разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.
Метод рандомизации (от англ. random— случайный, беспорядочный; в переводе на русский означает: перемешивание, создание беспорядка, хаоса) основан на принципе формального перевода систематических погрешностей в случайные. Этот метод позволяет эффективно уменьшать постоянную систематическую погрешность (методическую и инструментальную) путем измерения некоторой величины рядом однотипных приборов с последующей оценкой результата измерений в виде математического ожидания (среднего арифметического значения) выполненного ряда наблюдений. В данном методе при обработке результатов измерений используются случайные изменения погрешности от прибора к прибору. Поясним действие метода рандомизации простым примером. Пусть некоторая физическая величина измеряется п раз (число п достаточно велико) однотипными приборами, имеющими систематические погрешности одинакового происхождения. Для одного прибора эта погрешность — величина постоянная, но от прибора к прибору она изменяется случайным образом. Поэтому если измерить неизвестную величину и приборами и затем вычислить математическое ожидание всех результатов, то значение погрешности существенно уменьшится (как и в случае усреднения случайной погрешности). Рассмотрим некоторые методы, применяющиеся для обнаружения и уменьшения переменных и монотонно изменяющихся во времени систематических погрешностей.
Метод симметричных наблюдений весьма эффективен при выявлении и исключении систематической погрешности, являющейся линейной функцией соответствующего аргумента (амплитуды, напряжения, времени, температуры и т. д.). Положим, что измеряют физическую величину хu, а результаты наблюдений хi зависят от времени t. Для выявления характера изменения погрешности выполняют ряд наблюдений через равные промежутки времени Δt. Пусть выполнено пять наблюдений физической величины х1 – x5 в моменты времени t1 – t5.Вычислим средние арифметические значения двух пар наблюдений (х1 + х5)/2 и (x2 + x4)/2. Наблюдения в этих парах проведены в моменты t1, t5и t2, t4, симметричные относительно момента t3. При линейном характере изменения погрешности, полученные средние значения измеряемой величины должны быть одинаковы. Убедившись в этом, результаты наблюдений запишем как хi= хи+ kti, где к — некоторая постоянная. Пусть при измерениях получены значения х1 = хи + kt1 и х2 = хи + kt2. Решение полученной системы из двух уравнений дает значение измеряемой величины хи, свободное от переменной систематической погрешности:
xu = (x2t1 - x1t2) / (t1-t2) (4.5)
Метод анализа знаков неисправленных случайных погрешностей. Когда знаки неисправленных случайных погрешностей чередуются с некоторой закономерностью, имеет место переменная систематическая погрешность. Если у случайных погрешностей последовательность знаков «+» сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если же у случайных погрешностей группы знаков «+» и «-» чередуются, то имеет место периодическая систематическая погрешность.
Графический метод является наиболее простым методом, используемым для обнаружения переменной систематической погрешности в ряде результатов наблюдений. При этом методе рекомендуется построить график, на который нанесены результаты наблюдений в той последовательности, в какой они были получены. На графике через точки наблюдений проводят плавную линию, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.
36… Динамические погрешности измерения.
Динамическая погрешность измерений - погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
37Классификация сигналов. Детерминированные сигналы.
Сигналом называется материальный носитель информации, представляющий собой некоторый физический процесс, один из параметров которого функционально связан с измеряемой физической величиной. Такой параметр называют информативным.
Измерительный сигнал - это сигнал, содержащий количественную информацию об измеряемой физической величине. Основные понятия, термины и определения в области измерительных сигналов устанавливает ГОСТ 16465 70 «Сигналы радиотехнические. Термины и определения».
Измерительные сигналы чрезвычайно разнообразны. Их классификация по различным признакам.
По характеру измерения информативного и временного параметров измерительные сигналы делятся на аналоговые, дискретные и цифровые.
Сигнал - это любая физическая величина (например, температура, давление воздуха, интенсивность света, сила тока и т.д.), изменяющаяся со временем. Именно благодаря этому изменению сигнал может нести в себе какую-то информацию.
Электрический сигнал - это электрическая величина (например, напряжение, ток, мощность), изменяющаяся со временем. Вся электроника в основном работает с электрическими сигналами, хотя сейчас все больше используются световые сигналы, которые представляют собой изменяющуюся во времени интенсивность света.
Аналоговый сигнал - это сигнал, который может принимать любые значения в определенных пределах (например, напряжение может плавно изменяться в пределах от нуля до десяти вольт). Устройства, работающие только с аналоговыми сигналами, называются аналоговыми устройствами. Название "аналоговый" подразумевает, что сигнал изменяется аналогично физической величине, то есть непрерывно.
Цифровой сигнал - это сигнал, который может принимать только два (иногда - три) значения, причем разрешены некоторые отклонения от этих значений.
По степени наличия априорной информации переменные измерительные сигналы делятся на детерминированные, квазидетерминированные и случайные.
Детерминированный сигнал - это сигнал, закон изменения которого известен, а модель не содержит неизвестных параметров. Мгновенные значения детерминированного сигнала известны в любой момент времени. Детерминированными (с известной степенью точности) являются сигналы на выходе мер. Например, выходной сигнал генератора низкочастотного синусоидального сигнала характеризуется значениями амплитуды и частоты, которые установлены на его органах управления. Погрешности установки этих параметров определяются метрологическими характеристиками генератора.
Детерминированные и квазидетерминированные сигналы делятся на элементарные, описываемые простейшими математическими формулами, и сложные. К элементарным относятся постоянный и гармонический сигналы, а также сигналы, описываемые единичной и дельта-функцией.
Сигналы могут быть периодическими и непериодическими. Непериодические сигналы делятся на почти периодические и переходные. Почти периодическим называется сигнал, значения которого приближенно повторяются при добавлении к временному аргументу надлежащим образом выбранного числа почти периода. Периодический сигнал является частным случаем таких сигналов. Почти периодические функции получаются в результате сложения периодических функций с несоизмеримыми периодами.
Периодическим называется сигнал, мгновенные значения которого повторяются через постоянный интервал времени. Период Т сигнала параметр, равный наименьшему такому интервалу времени. Частота f периодического сигнала - величина, обратная периоду. Периодический сигнал характеризуется спектром. Различают три вида спектра:
комплексный комплексная функция дискретного аргумента, кратного целому числу значений частоты f периодического сигнала Y(t)
амплитудный - функция дискретного аргумента, представляющая собой модуль комплексного спектра периодического сигнала
фазовый - функция дискретного аргумента, представляющая собойаргумент комплексного спектра периодического сигнала
К тому же, как уже отмечалось, в природе все сигналы - аналоговые, то есть для преобразования их в цифровые и обратного преобразования требуется применение специальной аппаратуры (аналого-цифровых и цифро-аналоговых преобразователей). Так что ничто не дается даром, и плата за преимущества цифровых устройств может порой оказаться неприемлемо большой.
38… Временные характеристики стохастических сигналов.
Временные характеристики стохастических сигналов
Описание стохастических сигналов как функции времени в детерминированном виде невозможно. Вместо этого проводится статистическое описание. При этом предполагается, что сигнал является стационарным.
Первой
характеристикой стохастического сигнала
является амплитудная
плотность. Если амплитуды сигнала
разбить на интервалы
шириной ![]() ,
то можно определить
относительную частоту для
каждого интервала:
,
то можно определить
относительную частоту для
каждого интервала:
![]()
Аналогично
процедуре, изложенной ранее,
можно, осуществляя предельный
переход ![]() и Т
и Т![]() ,
получить в общем случае
непрерывную функцию амплитудной
плотности:
,
получить в общем случае
непрерывную функцию амплитудной
плотности:
![]() .
.
Среднее значение сигнала, определяемое в результате усреднения по времени, соответствует первому моменту плотности распределения, так как площадь под графиком плотности распределения равна единице:
![]()
Дисперсия сигнала
представляет собой среднеквадратичное отклонение
амплитуды от среднего значения. Это
величина соответствует
второму моменту плотности распределения
относительно
центра тяжести распределения ![]() :
:
![]() (7.1)
(7.1)
Разумеется, что характеристика сигнала c помощью только плотности амплитуд связана с известной потерей информации. Одному и тому же распределению плотности амплитуд может соответствовать бесконечное множество форм сигнала. И, что особенно важно, плотность амплитуд никак не характеризует тенденцию изменения сигнала во времени. Быстро изменяющийся сигнал может иметь то же самое распределение плотности амплитуд, что и медленно изменяющийся сигнал.
Корреляционная функция. Для оценки «тенденции сигнала к сохранению», которую также называют внутренней когерентностью, может быть использовано понятие корреляции.
При
изучении вопроса
о наличии линейной статистической связи
между парами значений ![]() и
и ![]() рассчитывают упомянутый
ранее коэффициент корреляции. Чем теснее
линейная зависимость,
тем больше модуль коэффициента корреляции,
тем с
большей вероятностью на основе значений
функции
в
момент времени
рассчитывают упомянутый
ранее коэффициент корреляции. Чем теснее
линейная зависимость,
тем больше модуль коэффициента корреляции,
тем с
большей вероятностью на основе значений
функции
в
момент времени ![]() возможен
прогноз
возможен
прогноз ![]() в
момент времени
в
момент времени ![]() .
Он состоит в том, что в течение отрезка
времени
.
Он состоит в том, что в течение отрезка
времени ![]() сигнал
имеет тенденцию к сохранению.
сигнал
имеет тенденцию к сохранению.
Изучаемый
отрезок времени
—
свободная (независимая) переменная.
Таким образом, коэффициент корреляции
является функцией
переменной
.
В рассматриваемом случае говорят об
автокорреляционной функции. В отличие
от коэффициента корреляции дискретных
пар значений автокорреляционная функция
в общем случае
относится к непрерывному сигналу ![]() и
часто не нормируется.
Как и при расчете среднего значения и
дисперсии,
сумма дискретных значений заменяется
интегралом
и
часто не нормируется.
Как и при расчете среднего значения и
дисперсии,
сумма дискретных значений заменяется
интегралом
![]() (7.2) Исходя
из изложенного, можно ожидать, что в
общем случае для больших сдвигов
времени
тенденция
к сохранению сигнала становится меньше.
Действительно, можно показать, что
(7.2) Исходя
из изложенного, можно ожидать, что в
общем случае для больших сдвигов
времени
тенденция
к сохранению сигнала становится меньше.
Действительно, можно показать, что ![]() есть
максимум функции и справедливо следующее
неравенство:
есть
максимум функции и справедливо следующее
неравенство:
![]() .
.
Как
следует из (7.2), ![]() (0)
=
(0)
= ![]() соответствует
среднему значению квадрата функции
соответствует
среднему значению квадрата функции ![]() :
:
![]()
Далее имеет место равенство
![]()
Для дисперсии, рассчитанной по (7.1), справедливо соотношение:
![]() .
.
Очевидно, автокорреляционная функция является четной функцией :
![]()
![]() является
характеристической функцией изучаемого
стохастического сигнала
.
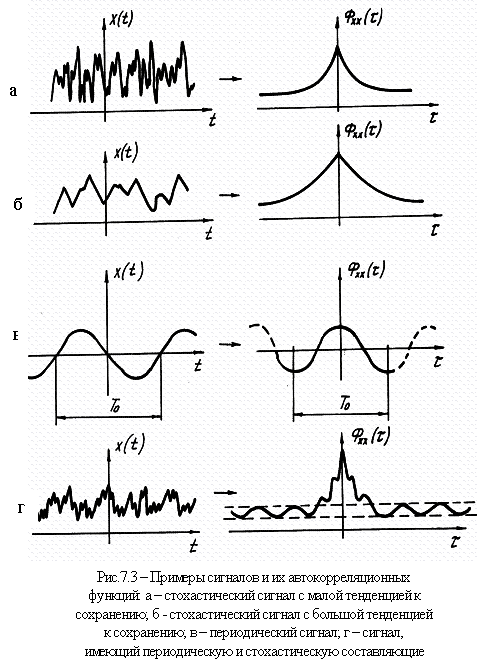
Тенденция сигнала к сохранению (рис.7.3,
а и б) характеризуется видом автокорреляции
одной функции между точками
является
характеристической функцией изучаемого
стохастического сигнала
.
Тенденция сигнала к сохранению (рис.7.3,
а и б) характеризуется видом автокорреляции
одной функции между точками ![]() и
и ![]() Если
Если ![]() то
это означает, что пары
значений
то
это означает, что пары
значений ![]() и
некоррелированы.
и
некоррелированы.
Разумеется, зависимость (7.2) можно применять и для стационарных детерминированных сигналов. Этим, априорно периодическим, сигналам соответствуют периодические автокорреляционные функции (рис.7.3, в).
Если сигнал содержит как периодическую, детерминированную, так и стохастическую составляющие, то в автокорреляционной функции при больших стохастическая составляющая сигнала становится некоррелированной, соответствующая ей составляющая автокорреляционной функции исчезает и остается только периодическая составляющая, соответствующая детерминированной составляющей сигнала (рис.7.3, г). Корреляция в этом случае отображает эффект фильтрации, что может быть использовано в измерительной технике.
39… Частотные характеристики периодического и апериодического сигналов.
Частотные характеристики периодического сигнала
Математическое описание и обработка гармонических сигналов осуществляются просто. В связи с этим периодический сигнал часто представляют в виде ряда Фурье, т. е. разлагают на гармонические составляющие. При этом гармонические составляющие могут быть описаны тремя равноценными способами. Для типовых периодических сигналов, таких как прямоугольные, пилообразные колебания и др., составлены таблицы соответствующих рядов Фурье.
7.5.1. Ряд Фурье как сумма синусоидальных и косинусоидальных колебаний. Ряд Фурье периодического сигнала по определению равен:
![]() ,
,
где ![]() -
круговая частота основной гармонической
составляющей:
-
круговая частота основной гармонической
составляющей:
![]() ;
;
![]()
Смысл
уравнения ряда
Фурье при
описании сигнала состоит в том, что вся
информация о сигнале
заключена
в амплитудах ![]() или
или ![]() как
функция дискретных частот
как
функция дискретных частот ![]() . Для
периодических функций
характерна дискретность амплитудных спектров
. Для
периодических функций
характерна дискретность амплитудных спектров ![]() и
и ![]() ,
т. е. они существуют
только при дискретных величинах
частоты
. Коэффициент
ряда Фурье
,
т. е. они существуют
только при дискретных величинах
частоты
. Коэффициент
ряда Фурье ![]() соответствует
так называемой постоянной составляющей
сигнала. Коэффициент
соответствует
так называемой постоянной составляющей
сигнала. Коэффициент ![]() отсутствует
в тех случаях, когда сигналы имеют вид
последовательности прямоугольных
импульсов.
отсутствует
в тех случаях, когда сигналы имеют вид
последовательности прямоугольных
импульсов.
7.5.2. Ряд Фурье как сумма косинусоидальных колебаний с различным сдвигом фаз. На основании тригонометрической теоремы сложения ряд Фурье можно записать в следующей форме:
![]()
где ![]()
![]()
При
этом описание сигнала
даётся
в виде дискретного амплитудного
спектра ![]() и
дискретного фазового спектра
и
дискретного фазового спектра ![]() .
.
7.5.3.
Ряд Фурье в комплексной форме. Наиболее
просто ряд Фурье описывается с помощью
комплексного коэффициента ![]() :
:
![]() ;
;
где ![]()
Используя уравнение Эйлера, можно показать, что
![]()
При
этом векторная величина
эквивалентна
величинам
и
или ![]() и
и ![]() :
:
![]()
![]()
