Основные уравнения гидродинамики

Уравнение неразрывности жидкости. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то можно записать:

или

где Q — расход жидкости, м³/с; v — средняя скорость в сечении при установив­шемся движении, м/с; S— площадь живого сечения, м²

Как следует из вышерассмотренного уравнения расход, проходящий через все живые сечения потока, неизменен, несмотря на то, что в каждом сечении средняя скорость и площадь живого сечения различны.

Уравнение называют уравнением неразрывности потока при установившемся движении.

Из уравнения получим важное соотношение

т. е. средние скорости обратно пропорциональны площадям живых сечений, которым соответствуют эти средние скорости.

Уравнение неразрывности потока — одно из основных уравне­ний гидродинамики. Оно выводится из уравнения неразрывнос­ти для элементарной струйки несжимаемой жидкости при уста­новившемся движении:

где v — местные скорости в каждом живом сечении струйки, м/с; S — площадь живого сечения элементарной струйки, м²;  Q_n— элементарный расход, м³/с

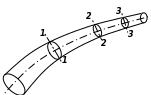
Рис.- схема демонстрирующая неразрывность потока

Уравнение Бернулли, его энергетическая и геометрическая ин­терпретации.

Рассматривая уравнение Бернулли для установив­шегося движения элементарной струйки идеальной жидкости, выделим в потоке жидкости элементарную струйку и определим удельную энергию жидкости. В идеальной жидкости при движе­нии не возникает сила трения, поэтому на основании закона сохранения энергии E₁=E₂.

Уравнение Бернулли для элементарной струйки идеальной жидкости имеет вид

Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удель­ная потенциальная энергия положения; Р/ — удельная потенциальная энергия давления; gz + Р/ — удельная потенциальная энергия; u²/2 — удельная кинети­ческая энергия; и — скорость элементарной струйки идеальной жидкости.

Энергетический смысл уравнения Бернулли: для элементар­ной струйки идеальной жидкости полная удельная энергия, рав­ная сумме удельной потенцальной энергии давления, удельной потенциальной энергии положения и кинетической удельной потенциальной энергии положения и кинетической удельной энергии, есть величина постоянная во всех сечениях по отноше­нию к выбранной плоскости отсчета.

Разделив уравнение на g, получим уравнение полного напора:

z - геометрическая высота или геометрический напор, м; P/ — пьезометрический напор или пьезометрическая высота, м; u²/(2g) —скоростной напор или скоростная высота, м; Н—полный напор, м.

Представим элементарную струйку идеальной жидкости с осью, проходящей через точки А, В и С (рис. а).

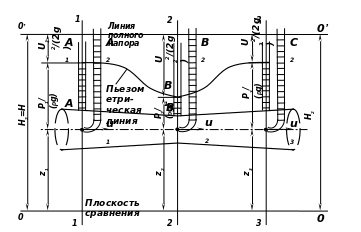
Рис. а . Графическая иллюстрация уравнения Бернулли для струйки идеальной жидкости

Точки А, В и С лежащие соответственно в сечениях 1—1, 2—2, 3—3, расположены на высоте z₁, z₂, z₃ над плоскостью сравнения О—О. Отложим от точки А вверх по вертикали отрезок АА₁, равный пьезометрической высоте Р₁/(g), а затем от точки А₁ вверх отрезок A₁A₂, равный u²/(2g), т. е. равный скоростному напору. Аналогичное построение проведем для точек В, С в сечениях 2—2, 3-3. Такое же построение можно повторить и для остальных точек оси элементарной струйки. Вершины полученных вертикальных отрезков АА₂, ВВ₂, СС₂ и т. д. должны находиться на одинаковой высоте от плоскости сравнения, т. е. должны лежать в одной горизонтальной плоскости 0'— 0', так как сумма трех членов

z+ Р/)+ u²/(2g) согласно уравнению ( ) вдоль всей . Струйки невязкой жидкости постоянна.

Для каждого сечения элементарной струйки полный напор Н это совокупность отрезков z , Р/) , u²/(2g). Соединив между собой концы отрезков Н, получим горизонтальную линию, которая называется линией полного напора. Линию изменения пьезометрических высот называют пьезометрической линией.

С геометрической точки зрения для движущейся идеальной жидкости уравнение Бернулли показывает, что сумма трех высот — геометрической, пьезометрической и скоростной — есть величина постоянная. Линия полного напора параллельна плоскости отсчета.

Умножив все члены уравнения ( ) на удельный вес жидкости , получим

z - весовое давление, Па; P — гидродинамическое давление, Па; и² /2 — динамическое давление Па; H — полное давление, Па.

Уравнение Бернулли для элементарной струйки реальной жидкости (рис. б):

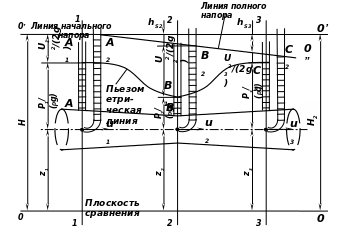
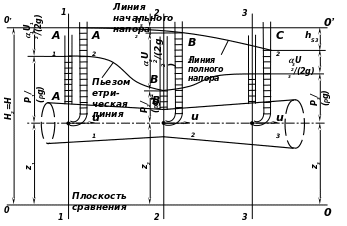
Рис. в . Графическая иллюстрация уравнения Бернулли для потока жидкости

где ghs - потерянная удельная энергия, Дж/кг, затраченная на преодоление сопротивлений движению, обусловленных трением в вязкой жидкости.

Остальные члены уравнения имеют то же значение, что и в уравнении для идеальной жидкости.

При рассмотрении движения струйки реальной (вязкой) жидкости гидродинамический напор в каждом предыдущем сечении будет больше гидродинамического напора в последующем сече­нии на величину потерь напора hs. Соответственно с этим напорная плоскость или силовая линия 0' - 0' оказывается наклонной (рис. 3.2, б).

Вторая форма записи уравнения для струйки реальной жидкости:

где с геометрической точки зрения ghs —потеря напора, м.

Линия полного напора представляет собой спадающую кри­вую.