Если , то если , то .

Эпюра давления будет в виде треугольника (рис. б). Следует отметить, что наклон линии зависит от величины . На­пример, для воды ( =9800 Н/м³) эпюра избыточного гидроста­тического давления будет представлять собой равнобедренный треугольник с углом =45°. Для жидкостей более тяжелых, чем вода (например, ртуть), наклон линии будет более пологим, т. е. <45°. Для жидкостей более легких, чем вода (например, бен­зин, спирт), наклон линии будет более крутым, т. е. >45°.

Принимая во внимание первое свойство гидростатического давления, получаем эпюру давления для плоской наклонной стен­ки (рис. б). Если стенка испытывает двустороннее давле­ние, то по тому же принципу можно построить эпюру для верти­кальной (рис. в) и наклонной (рис. г) стенок.

Если стенка имеет ломаный профиль, то эпюра будет иметь вид, представленный на рис д.

Cила избыточного гидростатиче­ского давления на дно сосуда зависит только от рода жидкости, площади дна сосуда и глубины жидкости в сосуде и не зависит от формы и объема сосуда. Это свойство жидкости известно под названием гидростатического парадокса (рис.).

Рис. . Схема к гидростатическому парадоксу.

Закон архимеда

Допустим, что тело произвольной формы погружено в жид­кость. Представим, что оно состоит из элементарных вертикаль­ных цилиндров, имеющих малые площадки ds. Верхние и ниж­ние основания цилиндров погружены на глубину h₁ и h₂ соответ­ственно. Причем элементарные силы гидростатического давления, направленные сверху и снизу , будут действовать на каждый из вышеуказанных цилиндров (рис.)

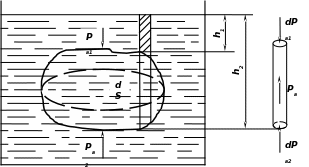
Как видно, h₁меньше h₂, это показыва­ет, что цилиндры находятся под действием элементарной вытал­кивающей силы dРв.

Для получения полной выталкивающей силы необходимо просуммировать элементарные выталкивающие силы. Значит, на тело, погруженное в жидкость, действует выталкивающая сила, равная по величине и обратная по направлению силе тяжести жидкости, вытесненной телом.

Этот закон, на котором основана теория плавания тел, установ­лен 2200 лет назад греческим ученым Архимедом и носит его имя.

Выталкивающую силу, приложенную в центре тяжести тела, называют выталкивающей(архимедовой) силой. Она направлена вертикально вверх и приложена в точке, соответствующей центру давления называемому - центром водоизмещения, количество воды, вытесненной плавающим телом, — водоизмещением.

Рис Плавучесть тела а и 6 — cудно остойчиво

На рисунке показана схема корпуса судна со следующи­ми обозначениями: а—а—плоскость плавания, ограниченная ватерлинией, как контуром; о—о—ось плавания—ось, нормаль­ная к плоскости плавания и проходящая через центр тяжести тела С.

На оси плавания расположены три центра: центр тяжести С, центр водоизмещения D и метацентр М (точка пересечения оси плавания с линией действия архимедовой силы).

Расстояние от метацентра до центра тяжести тела называют метацентрической высотой h_м. Приняв за плоскость сравнения – плоскость плавания охарактеризуем остойчивость.

При h_м > 0 положение тела будет остойчивым, при h_м < 0 — неостойчивым, а при h_м =0 тело будет находиться в состоянии безразличного равновесия.

Плавучесть и остойчивость — ключевые понятия теории плава­ния тел. Плавучесть — это состояние равновесия твердого тела, частично или полностью погру­женного в жидкость. Остойчи­вость — способность плаваю­щего тела, выведенного из рав­новесия, восстанавливать исходное положение после прекращения действия сил, вызывающих крен. Крен — положение тела, при котором вертикальная плоскость его симметрии отклонена от вертикали к земной поверхности.

Между соотношениями веса плавающего тела G и его вытал­кивающей силой Рв возможны три состояния тела, погруженного в жидкость.

Если G > Рв, то тело тонет, так как равнодействую­щая сил G и Рв направлена вертикально вниз.

Если G < Рв, тело плавает в полупогруженном состоянии (надводное плавание), и при этом равнодейст­вующая сил G и Рв направлена вертикально вверх, поэтому тело всплывает, пока новая уменьшенная выталкивающая сила Рв не будет равна весу тела G (G=Pv).

Тело плавает в погруженном состоянии в случае G=Pв, оно может находиться в устойчивом или неустойчивом равновесии. Чтобы тело находилось в равно­весии, необходимо, чтобы его центр тяжести и центр водоизме­щения лежали на одной вертикали.

В случае воздействия на плавающее тело внешних сил (ветра, крутого поворота) оно будет отклоняться от положения равнове­сия (давать крен). При остойчивом плавании тела центр тяжести расположен ниже центра водоизмещения, а после прекращения взаимодействия этих сил тело возвращается в прежнее положе­ние. При неостойчивом плавании центр тяжести тела располо­жен выше центра водоизмещения, В этом случае тело выведено из состояния равновесия и не может возвратиться в первона­чальное положение. Состояние безразличного равновесия харак­теризуется совпадением центров тяжести и водоизмещения.

Плавучесть тела выражается формулой

где G вес воды; в— удельный вес воды; V — объем вытесненной телом воды.