Поверхности равных давлений

Поверхность, во всех точках которой значения гидростатичес­кого давления равны между собой, называют поверхностью рав­ного давления или поверхностью уровня. На по­ложение уровня свободной поверхности влияют силы тяжести и инерции.

Найдем величину равного давления Р по трем частным произ­водным. При Р=const и р # 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид

Это уравнение называется уравнением поверхности жидкости равного или постоянного давления. Рассмотрим наиболее часто встречающиеся случаи.

Первый случай, когда на покоящуюся жидкость действует одна внешняя сила, сила тяжести, тогда , , (на­правление ускорения свободного падения не совпадает с положи­тельным направлением оси Z). В этом случае исходное уравнение имеет вид

или

т. е. получаем поверхности равного давления, представляющие собой семейство горизонтальных плоскостей. Каждому значению Z соответствует плоскость, точки которой имеют определенное постоянное значение давления. Свободная поверхность жидкости (для ограниченного объема), в данном случае—одна из плоско­стей равного давления. Имеем в виду, что свободная поверхность — это поверхность на границе жидкой и газообразной сред. На свободную поверхность будет приложено постоянное давление равное атмосферному.

Второй случай, когда поверхность равного давления может быть наклонной. Например, свободная поверхность бензина в железнодорожной цистерне, движущейся горизонтально с уско­рением а (рис)

В этом случае единичная масса жидкости находится под действием силы тяжести Z= -1 *g и горизонтального ускорения силы инерции Х= -1*а (к цистерне приложена си­ла с ускорением а, а к жидкости—такая же по величине сила инерции с ускорением - а).

Составляющие массовых сил в уравнении получают значения:

Из вышеизложенного следует, что свободная поверхность бен­зина в цистерне представляет собой плоскость с углом наклона

Уравнение в этом случае примет вид

После интегрирования получим зависимость распределения давления в любой точке цистерны с бензином:

Из этого выражения следует, что наибольшее давление будет в точке z=0 и максимальным отрицательным значением х.

Третий случай, когда жидкость находится в открытом ци­линдрическом сосуде, вращающемся вокруг его вертикальной оси с постоянной угловой скоростью а (рис).

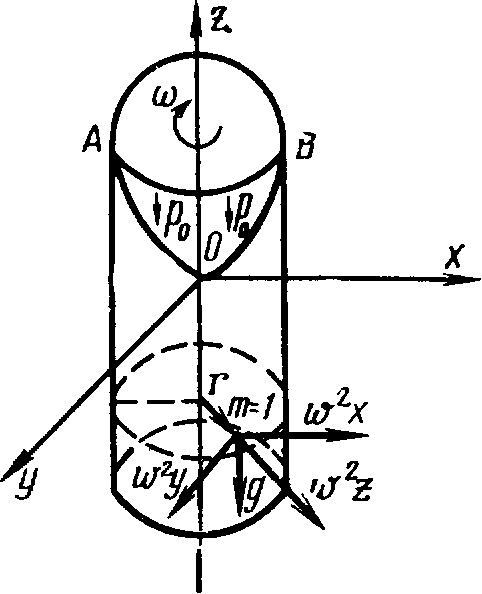
В этом случае на частицу жидкости массой m=l действуют сила тяжести G= -1*g, параллельная оси z, и центробежная сила F=1•v²/r=w²*r, перпендикулярная к оси z.

Из уравнения видно, что при вращении сосуда наи­большее давление будет в точках у дна и на боковых стенках сосуда.

Уравнение свободной поверхности можно получить при P==0

Кривая A—О—В—это па­рабола, а свободная поверх­ность жидкости — параболоид вращения. Такую же форму имеют и другие поверхности равного давления.

Основное уравнение гидростатики

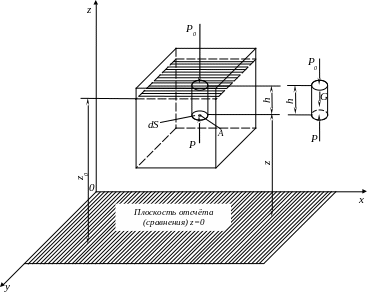
Рассмотрим объем жидкости, находящейся в покое под дейст­вием сил тяжести и давления на свободной поверхности. Опре­делим гидростатическое давление Р в т.А на бесконечно малой площадке dS, расположенной на глубине h от свободной поверхности жидкости и параллельной ей (рис. ). Выделим над этой площадкой некоторый цилиндрический объем жидкос­ти, заменив действие окружающей его среды силами давления на свободную поверхность РodS, на нижнее основание цилиндра РdS и на его боковую поверхность. Силы давления жидкости на боковую поверхность цилиндра взаимно уравновешиваются. На выделенный объем действует также массовая сила — вес G = g h dS. Цилиндр находится в равновесии, поэтому сумма проекций всех сил на ось z будет равна нулю:

Сократив члены этого уравнения на dS и перегруппировав их, получим основное уравнение гидростатики:

где P—полное или абсолютное давление, иногда обозначаемое как Pабс,gh — весовое давление, равное весу столба жидкости при единичной площа­ди и высоте h; z и z₀ — геометрические высоты расположения точек относительно произвольной горизонтальной плоскости называемой плоскостью сравнения

Если в уравнении заменить h на z-z₀, то получим

откуда при и

(для точек лежащих на свободной поверхности) имеем

т. е. другую форму записи основного уравнения гидростатики,

где P/g и P₀/g —высоты, соответствующие гидростатиче­скому давлению P и Pо. Величины z и P/g часто в гидрав­лике называют геометрической и пьезометрической высотами или геометри­ческим и пьезометрическим напорами.

Поскольку все слагаемые, входящие в уравнение

име­ют линейную размерность, то и сумма высот z+P/g будет также высотой Н с линейной размерностью. Высоту Н называют гидро­статическим напором. А горизонтальную плоскость, удаленную от плоскости сравнения на величину гидростатического напора Н называют плоскостью гидростати­ческого напора. Эта плоскость расположена выше плоскости свободной поверхности на высо­ту P₀/g . Итак, для данного объе­ма жидкости гидростатический напор относительно выбранной плоскости сравнения - величина постоянная:

С энергетической точки зрения рассматриваемое уравнение представля­ет собой постоянную величину суммы удельной потенциальной энергии положения z и удельной потенциальной энергии давле­ния P/g во всех точках покоящейся жидкости относительно плос­кости сравнения.

Из основного уравнения гидростатики следует, что гидростатическое давление Р в любой точке жидкости и на любой глубине h зависит от внешнего давления Ро на свободной поверхности, т. е. всякое внешнее давление, действующее на свободную поверхность жид­кости, находящейся в равновесии, передается внутрь во все точ­ки жидкости без изменения. В этом заключается закон Паскаля, найденный опытным путем и имеющий большое практическое значение.

Рассмотрим равновесие двух неоднородных жидкостей (g_{1 ¹} g₂ ), покоящихся в сообщающихся сосудах (рис. ):

если Ро₁ = Ро₂ = Ро, то h₁/h₂=g₂/g₁ ; h₁/h₂=r₂/r₁ т.е. неод­нородных жидкостях и одинаковом внешнем давлении в сообща­ющихся сосудах уровень жидкостей обратно пропорционален удельному весу этих жидкостей.

Для однородных жидкостей (g₂=g₁) свободная поверхность в сообщающихся сосудах устанавливается на одном уровне (h₁=h₂).