Малое (а) и затопленное (б) отверстия

В сече­нии 2—2 диаметр струи dc = 0,8do. Пропускная способность от­верстия So и степень сжатия струи Sc оцениваются коэффициен­том сжатия струи:

Отметим, что для круглого отверстия сжатое сечение находит­ся на расстоянии, примерно равном половине диаметра отверс­тия 0,5do. Если струя сжимается по всему периметру, то сжа­тие называют полным, а если отверстие находится на значи­тельном расстоянии от стенки и составляет не менее трех диа­метров отверстия, т. е. l > 3do, такое сжатие называют совер­шенным. Совершенное сжатие характеризуется наименьшими значениями коэффициентов сжатия и расхода.

Коэффициент совершенного сжатия на основании опытов для круглых и прямоугольных отверстий составляет e = 0,60... 0,64 (большим отверстиям соответствуют меньшие значения e, а меньшим — большие значения этого коэффициента). Наиболее часто применяют значения e = 0,64 при практических расчетах для малых отверстий в тонкой стенке. Несовершенное сжатие возникает в том случае, если расстояние от края стенки до контура отверстия находится на более близком расстоянии, т. е. l < 3do.

Чтобы вывести основные расчетные зависимости для опреде­ления скорости и расхода при истечении жидкости через малые незатопленные отверстия в тонкой стенке при постоянном напоре Н, составим уравнение Бернулли от произволь­ной горизонтальной плоскости сравнения О—О, проходящей через центр тяжести отверстия для двух сечений: сечения 1—1 на свободной поверхности жидкости в сосуде и сечения 2—2 по отверстию — там, где движение потока близко к плавно изменяющемуся движению (сжатое сечение струйки). Отметим, что ос­новное уравнение гидравлики — уравнение Бернулли — было получено именно в результате одного из подобных опытов (опубли­ковано в труде «Гидродинамика» в 1738 г.):

В этом уравнении z₁ = Н; z₂ = zc = 0. Если давление на сво­бодной поверхности в сосуде равно атмосферному, то p₁ = pс, причем V₁ и V₂ — средние скорости в соответствующих сечениях;

a₁ и a₂ — коэффициенты Кориолиса в сечениях 1—1 и 2—2; hs — потери напора между рассматриваемыми сечениями 1—1 и 2—2; как было показано выше, потери hs обусловлены только местными сопротивлениями самих отверстий, т. е.

где xо — коэффициент сопротивления отверстия.

При истечении с большими числами Рейнольдса Re>10⁵ зна­чение ^о = 0,06.

С учетом сделанных замечаний можно получить:

Обозначим , где Но — напор над центром тя­жести отверстия с учетом скорости подхода.

Тогда

Отсюда получим скорость истечения в сжатом сечении 2—2.

где коэффициент скорости. Численное значение j = 0,96...0,98.

Часто приходится иметь дело с истечением жидкости из за­крытого резервуара с давлением на свободной поверхности жид­кости p₁ в среду с давлением p₂; в данном случае скорость и расход жидкости определяют по формулам

где m— коэффициент расхода отверстия.

Если истечение происходит через затопленное отверстие (под уровень), т. е. не в газовую среду, а в смежный резервуар с той же жидкостью, то в качестве геометрического пара­метра принимают разность уровней жидкости в резервуарах H= H₁ — H₂, а скорость и расход определяют соответственно по формулам

Числовые значения коэффициентов сжатия и расхода при истечении под уровень те же, что и при истечении через неза­топленное отверстие, т. е. скорость и расход не зависят от высо­ты расположения отверстия.

При изучении истечения жидкости в атмосферу из малого отверстия в тонкой стенке представляет интерес явление, на­званное инверсией струи — изменение формы поперечного сече­ния струи по ее длине под действием сил поверхностного натя­жения на вытекающие криволинейные струйки и различных ус­ловий сжатия по периметру отверстия. Больше всего инверсия проявляется при истечении из некруглых отверстий.

Уравнение движения свободной струи жидкости, вытекающей из насадка, можно записать следующем образом:

|где q —угол между направлением истечения и осью абсцисс (рис.);

начальная скорость истечения; у—высота падения струи; х—дальность падения струи.

При q=0 получаем координаты осевой линии струи жидкости, вытекающей из малого вертикального отверстия в тонкой стенке:

Свободная струя жидкости, направленная вертикально вверх с начальной скоростью и, без учета сопротивления воздуха, сложных колебательных явлений, приводящих к раздроблению и в дальнейшем к распылению струи, поднимется на высоту

а — вертикальная; б — наклонная.

В незатопленных свободных струях различают компактную раздробленную и распыленную части. Компактная часть струи имеет форму отверстия, из которого, она вытекает, чаще всего цилиндрическую или близкую в ней. В раздробленной части происходит дробление струи на Отдельные крупные частицы. Распыленная часть струи состоит из отдельных мельчайших частиц жидкости.

Высота вертикальной струи /t/, включая распыленную часть, всегда меньше напора Н на величину потерь напора АА (рис. 1.48):

где d— диаметр насадка; k — коэффициент, получаемый опытным путем.

Истечение через насадки. Насадком называют короткую трубу (l = 3..4d), присоединенную к отверстию с целью изменения характеристик истечения жидкости.

Наиболее распространенными типами насадков являются:

• внешний цилиндрический насадок (насадок Вентури);

• внутрен­ний цилиндрический насадок (насадок Борда);

• конические на­садки (сходящийся и расходящийся);

• коноидальный насадок (на­садок криволинейного очертания);

• комбинированный или диффузорный насадок

Скорость и расход для всех видов насадков определяют по тем же зависимостям, что и для отверстия в тонкой стенке, т. е. для незатопленных насадков при постоянном напоре

а для затопленных насадков при постоянном напоре

где m — коэффициент расхода, зависящий от типа насадка; Но — напор над цент­ром тяжести выходного отверстия с учетом скорости подхода; h — разность уровней верхнего и нижнего бьефов с учетом скорости подхода.

Рассмотрим истечение жид­кости через внешний цилинд­рический насадок. При входе во внешний цилиндрический насадок в случае безотрывного режима истечения струя жид­кости сжимается, а затем рас­ширяется, заполняя все сече­ние насадка. При этом на вы­ходе из насадка диаметр струи равен диаметру отверстия и, следовательно, коэффициент сжатия e = 1.

Тогда коэффициент расхода

Коэффициент скорости для выходного сечения насадка

где коэффициент сопротивления насадка. Здесь xвх — коэф­фициент сопротивления входа; xв.р — коэффициент сопротивления внезапного расширения;l— коэффициент гидравлического трения в насадке; l, d— соответственно длина и диаметр насадка.

В результате расширения струи после сжатия и потерь по длине насадка коэффициент сопротивления при истечении из насадка значительно увеличивается по сравнению с истечением из отверстия.

При турбулентном режиме движения, когда число Рейнольдса достаточно велико, коэффициенты истечения для внешнего цилиндрического насадка m= f= 0,82; x= 0,5; e = 1.

Возрастание коэффициента сопротивления x до 0,5 приводит к увеличению потерь напора и уменьшению скорости истечения. Несмотря на это, расход жидкости при истечении через насадок превышает расход из отверстия » на 35%, что объясняется нали­чием вакуума в зоне сжатого сечения. По этой причине в сжатом сечении насадок работает как своеобразный насос, дополнитель­но подсасывая жидкость.

Величина вакуума может быть определена по формуле

Применение насадков. Насадки применяются в технике для различных целей. Для выпуска жидкости из резервуара и водое­мов применяют различные цилиндрические насадки. Для получе­ния больших выходных скоростей и дальности полета струи жид­кости применяют конически сходящиеся насадки в виде пожар­ных брандспойтов, форсунок для подачи топлива, гидромониторов для размыва грунта, фонтанных сопел, сопел гидравлических турбин. Наоборот, для замедления течения жидкости и увеличе­ния давления во всасывающих трубах гидравлических турбин, для замедления подачи смазочных масел применяют конически расходящиеся насадки.

Гидравлический удар. Комплекс явлений, возникающих в трубопроводе в связи с резким изменением скорости течения жидкости и сопровождающихся резким изменением давления Н. Е. Жуковский в 1898 г. назвал гидравлическим ударом.

При гидравлическом ударе повышение или понижение давления в трубопроводе объясняется инерцией массы жидкости. При быстром закрытии крана или задвижки частицы жидкости, со прикасающиеся с краном, мгновенно остановятся, что повлечет за собой значительное повышение ударного давления р вследствие уменьшения скорости до нуля (рис. ).

Скорость движения частиц жидкости непосредственно у крана будет погашена, а кинетическая энергия потока будет израсходована на работу деформации сжатия жидкости и растяжения стенок трубы.

В результате сжатия жидкости давление в ней увеличится , величину DР. Тогда возникшая у крана ударная волна (сечения п—п) отделит поток жидкости с давлением Р +DР и скоростью v = 0 от потока с давлением Р и скоростью v.

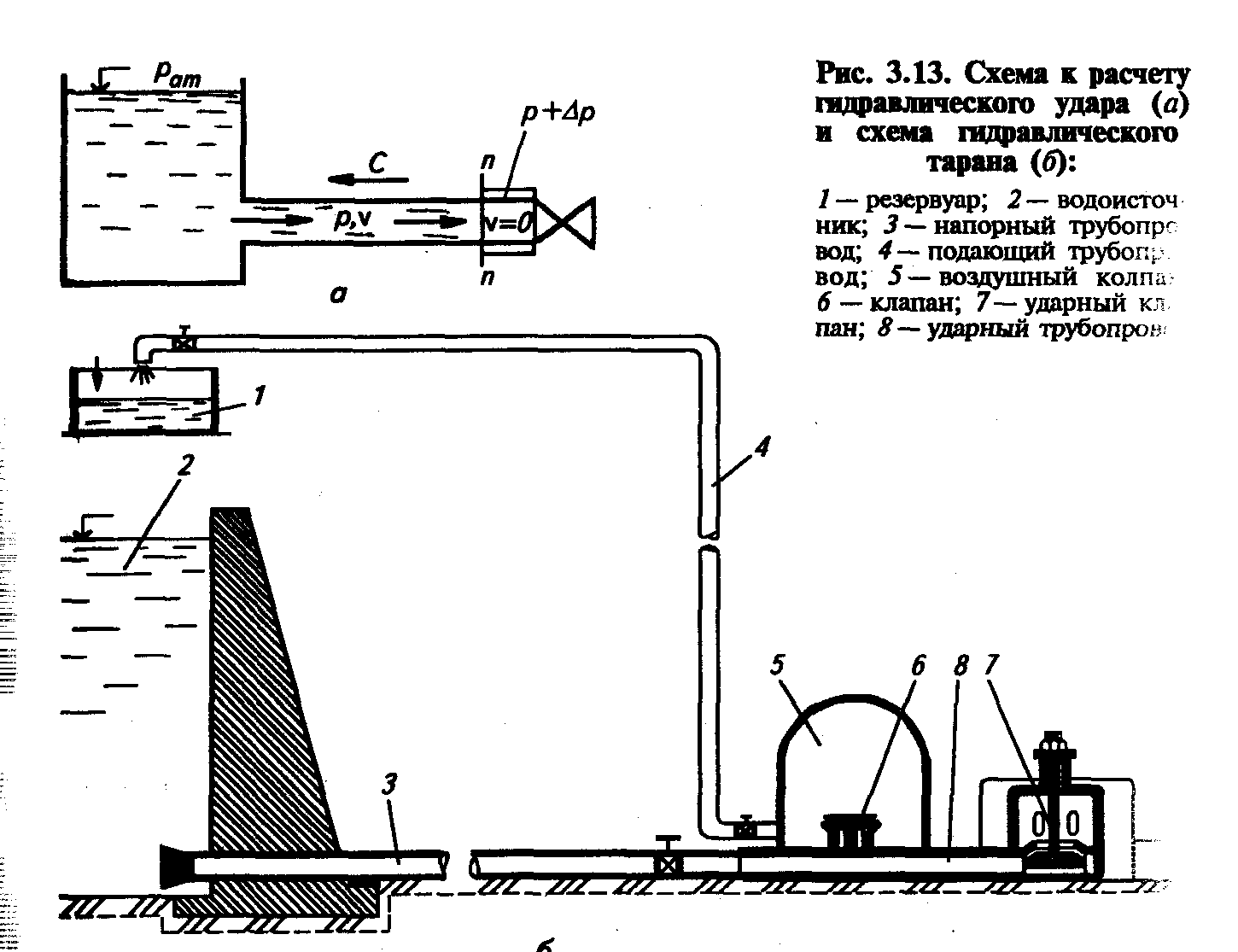
У крана на остановившиеся частицы жидкости набегают другие, при этом они также теряют свою скорость, вследствие чего сечение п—п передвигается от крана к резервуару трубопровода Когда ударная волна достигнет резервуара, вся жидкость в трубе будет остановлена и сжата, т. е. во всей трубе скорость буде равна нулю, а давление увеличится и составит Р +DР. Этот период называют периодом повышения давления, причем скорость распространения ударной волны определяется по формуле а = l/Dt где Dt — время, за которое сечение п—п пройдет по длине трубопровода l от крана до резервуара. Вышеописанное состояние не является равновесным. В следующий момент вре­мени жидкость начинает поступать из трубы в резервуар, причем сначала начнет двигаться обратно слой жидкости, ближайший к резервуару. Постепенно вся жидкость придет в движение по направлению от трубы к резервуару. Сечение п—п теперь переме­щается в обратном направлении — к крану с той же скоростью v, оставляя за собой выравненное давление P и скорость v, направ­ленные в сторону резервуара.

При достижении ударной волной крана (конец второго периода — периода восстановления) расположенный непосредственно у крана слой жидкости будет стремиться оторваться от него, в результате чего давление понизится на DР, жидкость расширится, а стенки трубопровода сожмутся. Вследствие этого возникнет отрицательная ударная волна непосредственно у крана, распро­страняющаяся со скоростью v по направлению от крана к резер­вуару и оставляющая позади себя давление Р — DР, причем ско­рость v = 0. Этот третий период называют периодом понижения давления.

Четвертый период характеризуется восстановлением давления и после прихода ударной волны к резервуару — возобновлением движения жидкости к крану. Такое движение жидкости продол­жается до тех пор, пока колебания не затухнут из-за потерь энергии на трение и деформацию стенки трубы.

Время, необходимое для того, чтобы ударная волна, исходя­щая из крана, вернулась к нему, называют временем фазы. В зависимости от соотношения времени закрытия крана и времени фазы удара различают прямой и непрямой гидравлические удары. Гидравлический удар называют прямым, если время за­крытия крана меньше времени фазы (tз < tф), и непрямым, если время закрытия крана больше времени фазы (tз > tф), т.е. при возвращении ударной волны к крану он еще полностью не за­крыт.

Повышение давления в трубе определяют по формуле Жуков­ского:

при прямом ударе

где r— плотность жидкости, кг/м³; а — скорость распространения ударной волны м/с; v — скорость движения жидкости в трубе до закрытия крана, м/с;

при непрямом ударе

где vo — скорость движения жидкости в трубе до частичного закрытия крана.

Для устранения причин, вызывающих гидравлический удар в трубопроводах, применяют постепенно закрывающиеся гидрав­лические задвижки разных конструкций, а также устанавливают различного рода компенсаторы ударного давления. Примером использования гидравлического удара для полезных целей явля­ется гидравлический таран или водяной насос (рис.).

ДВИЖЕНИЕ ЖИДКОСТИ В КАНАЛАХ И БЕЗНАПОРНЫХ ВОДОВОДАХ. ФИЛЬТРАЦИЯ

Особенность движения жидкости в каналах и без­напорных водоводах состоит в том, что оно безнапорное (сво­бодная поверхность потока соприкасается с атмосферой) и рав­номерное (живые сечения, средняя и местная скорости движе­ния потока одинаковы).

Каналы и безнапорные водоводы применяют во многих от­раслях народного хозяйства: сельском хозяйстве, гидроэнергети­ке, водном транспорте, в промышленности. Многие каналы и во­доводы имеют комплексное назначение.

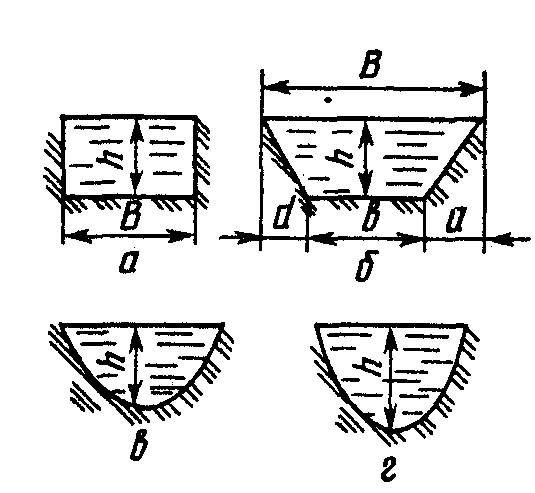
Каналы бывают (рис. ) прямоугольного сечения (а), тра­пецеидального (б), полукруглого (в) и параболического (г).

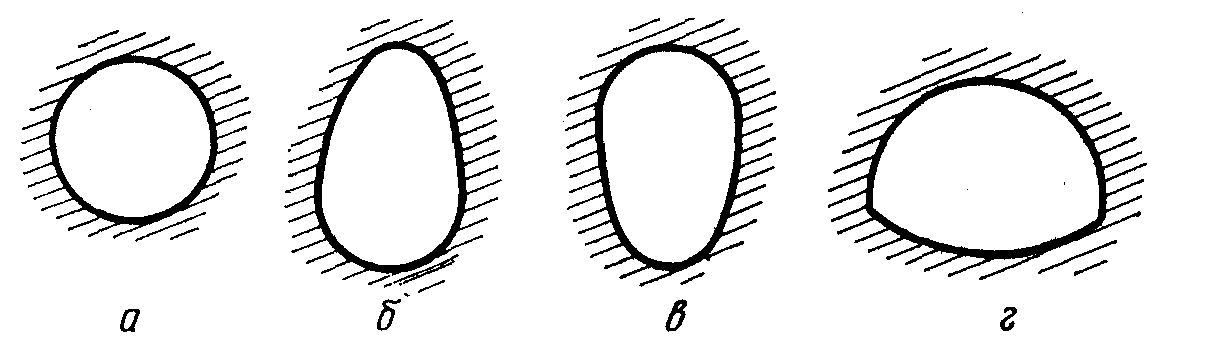
Водоводы выполняются замкнутыми (рис. ) и имеют стан­дартные профили круглого (а), шатрового (б), овоидального (в) и лоткового сечения (г)

Типы поперечных сечений водоводов: