Гидравлический расчет трубопроводов

Для транспортирования жидкостей используют трубопрово­ды, изготовленные из разных материалов. Они бывают напо­рными и безнапорными, короткими и длинными, простыми и сложными.

Простые трубопроводы. Простым (коротким) называют тру­бопровод, по которому жидкость транспортируют от питателя к приемнику без промежуточных ответвлений потока. При этом необходимо учитывать не только потери напора на трение по длине трубопровода, но и скоростной напор и местные потери напора, которыми в данном случае нельзя пренебречь.

Исходным при расчетах простого трубопровода (рис. )

яв­ляется уравнение баланса напоров (уравнение Бернулли)

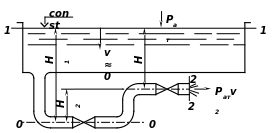
Схема к расчету короткого трубопровода

Учитывая, что v²₁/2g=0, Н₁— H₂= H; v₂ = v₁ и

получим

откуда средняя скорость исте­чения жидкости

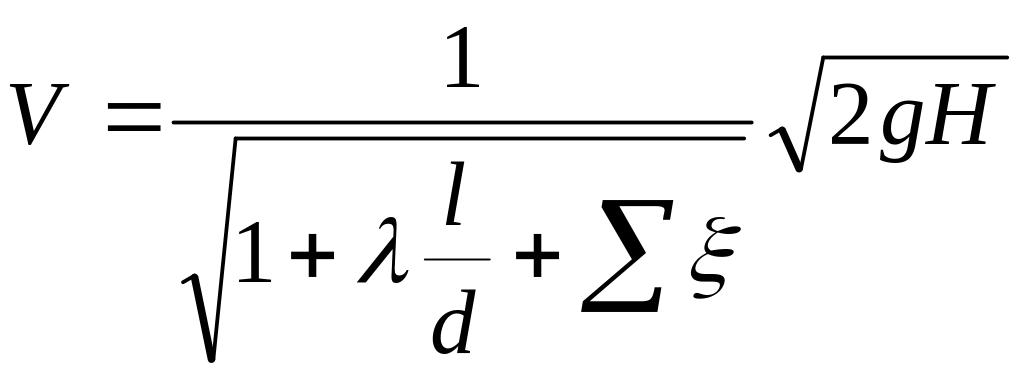
Введем обозначение 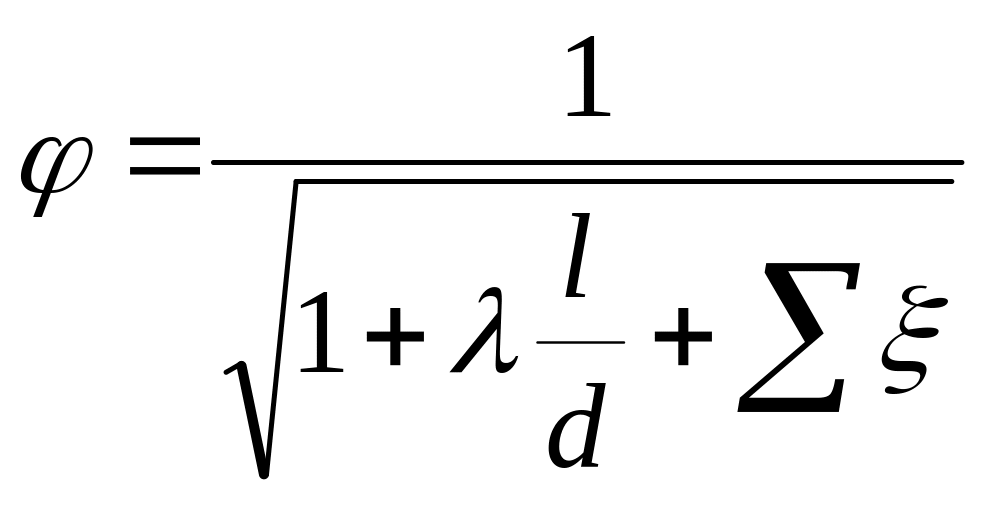где — коэффициент скорости, а

— коэффициент сопротивления системы

Следовательно, окончательно

Расход жидкости, пропускаемой через короткий трубопровод, можно определить по формуле

где =— коэффициент расхода; S— площадь живого сечения.

Длинные трубопроводы. Это трубопроводы постоянного по длине диаметра, у которых основными являются потери напора по длине, а местными потерями напора и скоростным напором можно пренебречь.

Потери напора по длине трубопровода определяют

по формуле Дарси—Вейсбаха:

Учитывая, что расход Q = VS и скорость движения потока тогда

или

где А — удельное сопротивление трубопровода, определяемое по справочным таблицам;

Для переходной области удельное сопротивление Ао=А,

где  — поправочный коэффициент, учитывающий зависимость коэффициента |гидравлического трения  от числа Рейнольдса.

Кроме удельного сопротивления А в литературе по гидравлике для решения задач приводится способ расчета длинных трубо­проводов, базирующийся на формуле Шези.

Широко применяемые гидравлические параметры — это мо­дуль расхода , сопротивление трубопровода S_T=A*l, про­водимость трубопровода . С помощью вышеука­занных параметров потери напора по длине можно определить следующим образом:

Параллельное соединение трубопроводов. В узел поступает рас­ход Q и разделяется на n в общем случае неравных частей Q₁ , Q₂ , Оз, ..., Qi, ..., Qn.

Особенность расчета заключается в том, что потери напора в каж­дой из линий одинаковы и равны разности напоров в узлах А и B.

h₁= h₂ = h₃ = ... = h_n = h_A - h_B

Расход через любую из линий, соединяющих точки А и В, может быть записан в виде

Так как сумма расходов во всех параллельных трубопроводах равна расходу Q до разветвления трубопровода

Последовательное соединение трубопроводов. Рассмотрим тру­бопровод, состоящий из п последовательно соединенных труб различных диаметров. Каждый участок этого трубопровода имеет длину l и диаметр d.

При движении жидкости по трубопроводу весь напор Н будет затрачен на преодоление потерь напора по длине.

Полная потеря напора в трубопроводе равна сумме потерь на отдельных участках

где l — длина участка, м; A — удельное сопротивление участка.

Трубопроводы с равномерно распределенным путевым расходом.

Это такие трубопроводы, в которых вдоль всего пути расход

Расход в сечении А (рис. )

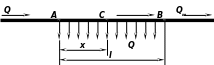
Схема к расчету трубопрово­да с путевым расходом

где Q_Т — транзитный расход; Qn — путевой расход.

Отношение путевого расхода Qn к длине трубопровода l назы­вают удельным расходом q.

Расход в произвольном сечении С, расположенном на рассто­янии х от начального сечения А,

Потери напора при Q_T  0:

Рассмотрим трубопровод постоянного диаметра, у которого расход непрерывно изменяется по его длине. Это вызвано тем, что кроме транзитного расхода существует путевой расход. Объ­емный расход по длине участка с путевым отбором будет пере­менным:

На участке АВ, где имеется непрерывный путевой расход, определим потери напора в трубопроводе (см. рис. ). Обо­значим расходы: транзитный Q_T, путевой Qn и удельный q. Отно­шение путевого расхода к длине трубопровода (удельный расход) q = Qn/l. Под удельным расходом q понимают количество Жидкости, отдаваемой на сторону через отверстия в каждой единице длины трубопровода.

Из схемы видно, что расход в сечении А

С течением времени расход постепенно уменьшается и стано­вится равным Q_T в сечении В, а в произвольном сечении С расположенном на расстоянии х от начального сечения А расход жидкости

Потери напора по длине в трубопроводе для квадратичной области турбулентного режима

Если на участке АВ будет отобран весь расход, т. е. отсутству­ет транзитный расход (Q_T = 0), то потери напора по длине в данном частном случае примут вид формулы, которая носит название формулы Дюпуи:

В случае расчета трубопроводов с путевым расходом с достаточной степенью точности Qп² /3 можно заменить членом Qп² /4. Тогда

Расчетный расход на участке АВ

Анализ этой формулы показывает, что путевой расход Qп эквивалентен транзитному расходу и зависит от степени равно­мерности отбора жидкости по длине трубопровода.

Сложные трубопроводы. Такой трубопровод имеет разветвлен­ные участки, состоящие из нескольких труб (ветвей), между ко­торыми распределяется жидкость, поступающая в трубопровод из питателей. Сечения трубопроводов, в которых смыкаются не­сколько ветвей, называют узлами.

Расчет сложных трубопроводов можно разделить на три ос­новные группы, когда задачей его является определение:

1. раз­меров труб по заданным в них расходам и перепадам напоров в питателях и приемниках;

2. перепадов напоров в питателях и приемниках по заданным расходам в трубах заданных размеров;

3) расходов в трубах заданных размеров по известным перепадам напоров.

При расчете сложных трубопроводов составляют систем уравнений, которая устанавливает функциональные связи между параметрами, характеризующими потоки жидкости в трубах, т.е. между размерами труб, расходами жидкости и напорами. Эта система состоит из уравнений баланса расходов для каждого узла и уравнений баланса напоров (уравнений Бернулли) для каждой ветви трубопровода.