Гидравлические сопротивления

При движении жидкости в трубах и других водотоках энергия потока расходуется на преодоление сопротивлений движению (потери напора). Возникающие при движении жидкости сопротивления (так называемые гидравлические сопротивления) можно разделить на два вида: 1) сопротивления по длине, обусловленные силами трения; 2) местные сопротивления, обусловленные изме­нениями скорости потока по величине и направлению.

Основной закон вязкого сопротивления.

Возможны два резко отличающихся режима движения жидкостей: ламинарный и турбулентный. Существование двух режимов движения подтверждено экспериментально в 1883 г. известным английским ученым Осборном Рейнольдсом.

Рис. 3.3. Режимы движения жидкости: а – схема прибора Рейнольдса; 1,3,5 - сосуды с жидкостью; 2 – труба; 4 – вентиль; б – ламинарный режим; в – турбулентный режим.

Схема прибора для демонстрации режимов движения показана на рис.

Ламинарное (параллельно-струйное) движение (от латинского lamina — лист, полоса) — строго упорядоченное, j слоистое движение без перемешивания жидкости (рис. б). | Пьезометр, присоединенный к трубе с установившимся ламинарным движением, показывает неизменность давления и скорости во времени, отсутствие колебаний (пульсаций).

Турбулентное (беспорядочное) движение (от латинского turbu-lentus — бурный, беспорядочный) характеризуется интенсивным перемешиванием частиц жидкости и пульсациями скоростей и давлений. При турбулентном режиме движения наряду с основным продольным движением жидкости вдоль трубы наблюдаются поперечные перемещения и вращательное движение отдельных объемов жидкости (рис. 3.3, в).

Изменение режимов движения жидкости в трубе наблюдается при определенной скорости потока, которую называют критической V_Kp.

Рейнольдс установил, что критическая скорость прямо пропорциональна кинематической вязкости жидкости V и обратно пропорциональна диаметру трубы d, т. Е.

где k- безразмерный коэффициент пропорциональности, или критическое число Рейнольдса

При практических расчетах для круглых труб постоянного диаметра Rе_кр=2320.

Безразмерный параметр, представляющий собой произведение фактической скорости движения жидкости v на диаметр трубы d, деленное на кинематическую вязкость жидкости v, называют критерием или числом Рейнольдса:

При Re<Re_Kp = 2320 режим движения жидкости ламинарный,

а при Re>Re_Kp = 2320 — турбулентный.

Сопротивлеиия трения по длине. Схема для расчета сопротивления трения по длине представлена на рис..

Потери напора по длине (или потери на трение, путевые потери) при напорном движении в круглых трубах определяют по формуле Дарси—Вейсбаха:

где _тр- коэффициент сопротивления движению жидкости по длине трубы;

_тр=l /d, здесь -безразмерный коэффициент гидравлического трения (коэффициент сопротивления участка круглой трубы длиной, равной ее диаметру);l— общая длина трубы; d— диаметр трубы.

Зависимость гидравлического коэффициента от режима движения жидкости и шероховатости стенок.

При ламинарном режиме формула Пуазейля

Таким образом, коэффициент гидравлического трения обрат­но пропорционален числу Рейнольдса Re.

Если для ламинарного режима коэффициент  в полной мере определяется числом Re, то для турбулентного  зависит и от шероховатости внутренней поверхности трубы. Шероховатость характеризуется величиной и формой разных по размеру выступов и неровностей, имеющихся на поверхности стенок; на неё влияют также материал стенок и чистота обработки их поверхности.

Основная характеристика шероховатости трубы — абсолютная шероховатость — средний размер выступов и неровностей, измеренный в единицах длины. |

При турбулентном режиме большая часть потока в трубе занята турбулентным ядром, а у стенок трубы образуется очень тонкий пограничный слой с ламинарным подслоем. В пределах этого ламинарного подслоя скорость резко возрастает от нуля на стенке трубы до некоторой конечной величины v_л на его границе. Толщина _л ламинарного подслоя очень мала. При увеличении скорости потока толщина _л уменьшается, и при больших числах Re ламинарный подслой практически исчезает (рис. б).

Если размер выступов шероховатости меньше толщины ламинарного подслоя, т. е. < _л, то труба называется гидравлически гладкой и коэффициент гидравлического трения , зависит только от числа Re и не зависит от шероховатости стенок.

Если высота выступов превышает толщину ламинарного подслоя т.е. >_л, то трубы называются гидравлически шероховатыми

Относительная шероховатость — отношение абсолютного размера выступов шероховатости к радиусу или внутреннему диаметру трубы,

т. е. /r или /d.

Когда все выступы шероховатости имеют одинаковую форму, то это равномерно распределенная зернистая шероховатость.

В условиях турбулентного режима можно выделить три области гидравлического сопротивления:

Область гидравлически гладких труб

Существует ряд эмпирических и полуэмпирических формул для определения коэффициента  гидравлически гладких труб. Одной из наиболее удобных является формула Блазиуса:

2. Докввадратичная, или переходная, область, где

причем

Коэффициент , можно также определить, например, по формуле А.Д. Альтшуля:

Переходная область сопротивлений является промежуточной и характеризуется тем, что размер выступов шероховатости примерно равен толщине ламинарного подслоя.

3. Квадратичная, или область гидравлически шероховатых труб

причем Re> 1100d/

Коэффициент  можно также рассчитать по формуле Никурадзе:

или Шифринсона:

Для определения коэффициента гидравлического трения при турбулентном режиме имеется еще большое число различных формул. Например, универсальная формула для определения , имеет вид

где d — расчетный внутренний диаметр трубы.

При скорости меньше 1,2 м/с в формулу вводится поправоч­ный коэффициент:

Кроме того, есть графики для определения  (И. И. Никурадзе) (рис в).

Местные потери напора при турбулентном движении жидкости.

В результате изменения величины или направления скорости движения жидкости на различных участках трубопровода появля­ются местные потери напора: внезапное расширение или суже­ние потока, резкие повороты, при прохождении

через краны (рис. а), диафрагмы (рис. б),

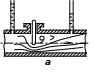
задвижки, вентили и т. д., — поэтому часть напора удельной энергии затрачивается на то, чтобы преодолеть сопротивление движению жидкости, а часть механической энергии превращается в теплоту.

Общих теоретических формул для нахождения коэффициен­тов местных сопротивлений , за исключением отдельных случа­ев, нет. Поэтому эти коэффициенты обычно определяют экспе­риментальным путем и выражают в виде эмпирических формул, графиков или таблиц.

Простейшие местные гидравлические сопротивления можно разбить на три группы: расширение, сужение, поворот русла.

При внезапном расширении трубопровода от диаметра d₁ до диаметра d₂ поток, вытекающий из узкой трубы, не сразу заполняет все поперечное сечение широкой трубы, а отрывается от стенок и движется в виде расширяющейся струи, пока не заполнит все сечение трубы с большим диаметром. В кольцевом пространстве между струёй и стенкой широкой трубы образуются вихри. Из-за отрыва потока и вихреобразования с непрерывным обменом частицами жидкости между основным потоком и завихренной его частью происходит переход механи­ческой энергии в тепловую, что является причиной значитель­ных потерь напора (рис. в).

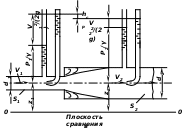
Потери напора при внезапном расширении могут быть опре­делены по формуле Борда:

где V₁ и V₂ — соответственно средние значения скорости до и после расширения трубопровода.

После преобразований получим

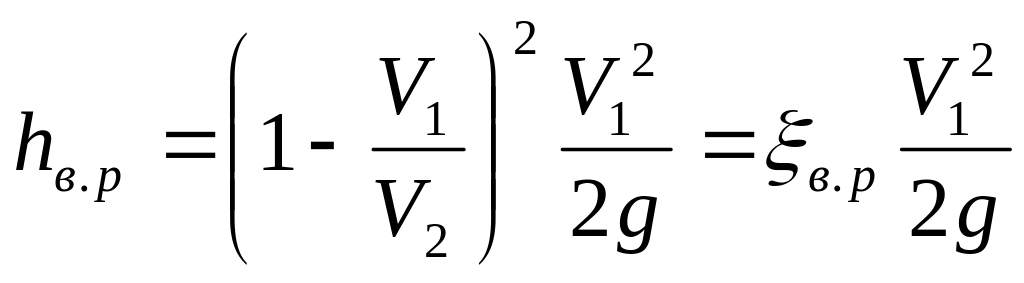где

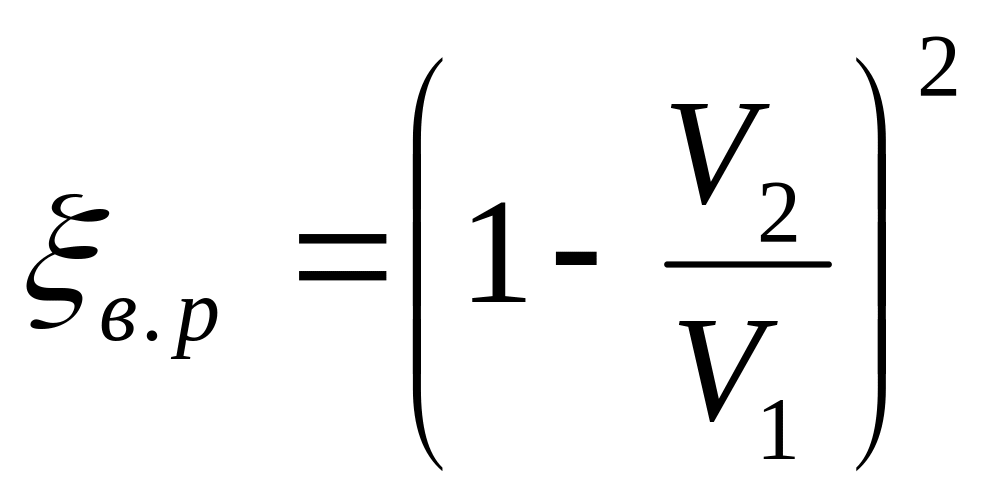
- коэффициент местного сопротивления для внезапного рас­ширения.

Согласно уравнению неразрывности потока

поэтому можно записать

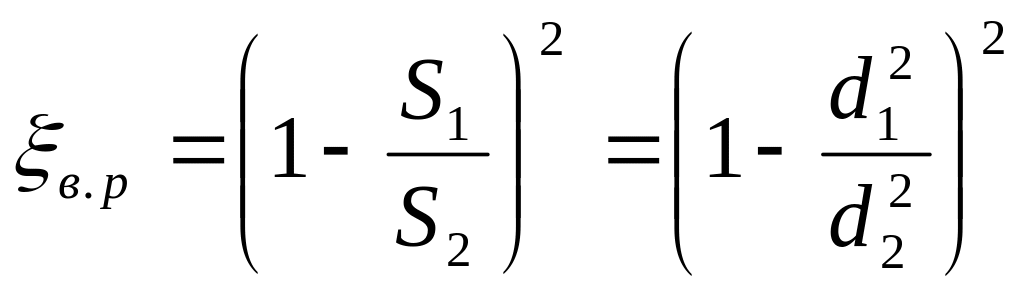
Если потери напора при внезапном расширении выразить через скорость V₂, т. е.

тогда

При внезапном сужении трубопровода от диаметра d₁ до диаметра d₂ поток сужается постепенно, при этом жидкость не обтекает входной угол, а срывается с него и на некотором расстоянии от внезапного сужения достигает наименьшей пло­щади Sс, вокруг которой образуется вихревая кольцевая зона. Затем поток начинает постепенно расширяться до площади жи­вого сечения, равной поперечному сечению узкого трубопровода диаметром d₂ (рис. г).