Уравнение бернулли для потока вязкой жидкости

При переходе от элементарной струйки к потоку вязкой жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей в живых се­чениях и иметь представление о случаях возможного и невоз­можного применения уравнения Бернулли.

Решение этих вопросов сводится к установлению поправоч­ных коэффициентов  и выделению потоков с плавно изменяю­щимся движением, т. е. таким движением, при котором угол расхождения между соседними элементарными струйками на­столько мал, что составляющими скорости в поперечном сече­нии можно пренебречь. В этих условиях справедлив основной закон гидростатики, т. е. величина z+Р/ одинакова во всех точках сечения.

При движении вязкой жидкости вдоль твердой стенки ее скорость достигает максимального значения в центральной час­ти потока и уменьшается до нуля возле стенки. Неравномерное распределение скоростей означает неодинаковое скольжение одних элементарных струек по другим, движение вязкой жид­кости сопровождается вращением частиц, вихреобразованием и перемешиванием. Поэтому приходится вводить среднюю по сечению скорость v. Для приведения результатов расчетов по средней скорости в соответствие с действительными скоростями вводится коэффициент Кориолиса , характеризующий неравно­мерное распределение скоростей в живом сечении потока, пред­ставляющий собой отношение кинетической энергии, подсчитан­ной по истинным скоростям сечения, к той же энергии, вычисленной по соседней скорости в этом же сечении потока:

где М—масса жидкости; и и v—соответственно истинная и средняя ско­рости.

Обычно в трубопроводах и каналах  = 1,05... 1,1. Иногда приближенно принимают a  1.

Поэтому для потока вязкой жидкости с учетом неравномер­ности распределения скоростей по живому сечению уравнение Бернулли запишется следующим образом:

Уравнение Бернулли устанавливает связь между высотны­ми положениями частиц жидкости, давлением и скоростями в разных сечениях потока жидкости. Причем каждая из входя­щих в уравнение величин может изменяться, но сумма их остается постоянной.

Падение полной удельной энергии жидкости вдоль потока, приходящегося на единицу его длины l, называют гидравлическим уклоном J и определяют по формуле

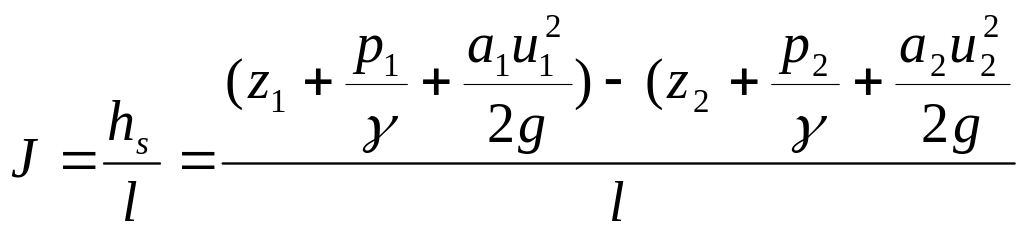
Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.

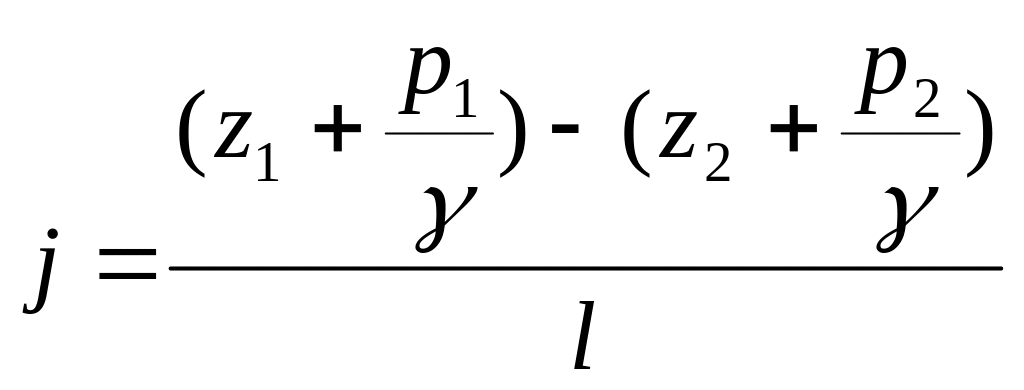
Если гидравлический уклон всегда положителен, то пьезомет­рический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока v² / (2g) = const. Следовательно, пьезометрическая линия параллельна энергети­ческой, и пьезометрический уклон равен гидравлическому.

Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, назы­вают геометрическим уклоном i и определяют по формуле

где l — расстояние между сечениями потока.

Сформулируем два условия применимости к потоку жидкости уравнения Бернулли: 1) движение жидкости должно быть установившимся; 2) движение жидкости в сечениях 1—2, 2—2 и 3—3,cоединяемых уравнением Бернулли, должно быть параллельно струйным или плавноизменяющимся, в промежутке же между сечениями 1—1, 2—2 и 3—3 движение жидкости может быть и резко меняющимся.

Hа применении уравнения Бернулли основан принцип действия приборов для измерения скоростей и расходов жидкости. Одним из таких приборов является расходомер Вентури, состоящий из двух конических отрезков трубы, узкие концы которых соединены коротким цилиндрическим патрубком длиной менее 10 диаметров трубопровода (отношение диаметра конфузора и диффузора соответственно d/D=^:0,3...0,7). Принцип работы расходомера Вентури базируется на уравнении Бернулли и уравнении неразрывности потока, а также на том, что перепад давлений на диафрагме, измеряемый пьезометром либо дифманометром пропорционален квадрату протекающего через нее расхода

Для определения местных скоростей при плавноизменяющемся безнапорном движении применяют метод Пито. Трубку, нижний конец которой изогнут под прямым углом, опускают навстречу потоку, и жидкость в трубке начинает подниматься над свободной поверхностью, где давление равно атмосферному, на высоту .

При определении местных скоростей в напорном потоке используют систему из двух трубок, одна из которых представляет собой обычный пьезометр, показывающий напор Р/, а другая,только что описанная, измеряет величину напора

Разность уровней в обеих трубках h представляет собой скоростной напор

Местные скорости находят с помощью трубки Пито по формуле

где k- поправочный коэффициент, определяемый для каждой трубки опытным путем