
Контрольное задание № 1.1
1. Найти область определения функции:
![]() .
.
2. Построить линию:
![]() .
.
3. Найти пределы функций:
3.1.
![]() ;
3.2.
;
3.2.
 ;
3.3.
;
3.3.
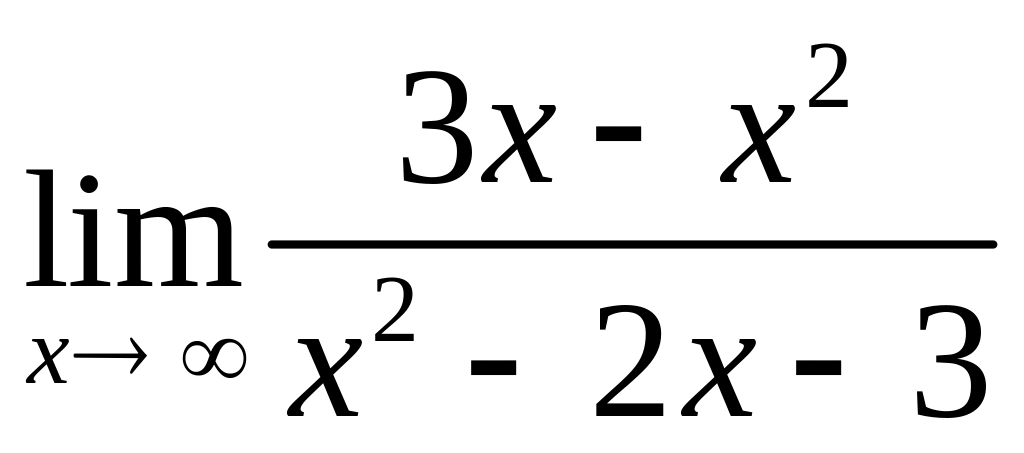 ;
;
3.4.
 ;
3.5.
;
3.5.
 ;
3.6.
;
3.6.
 ;
;
3.7.
![]() ;
3.8.
;
3.8.
![]() ;
3.9.
;
3.9.
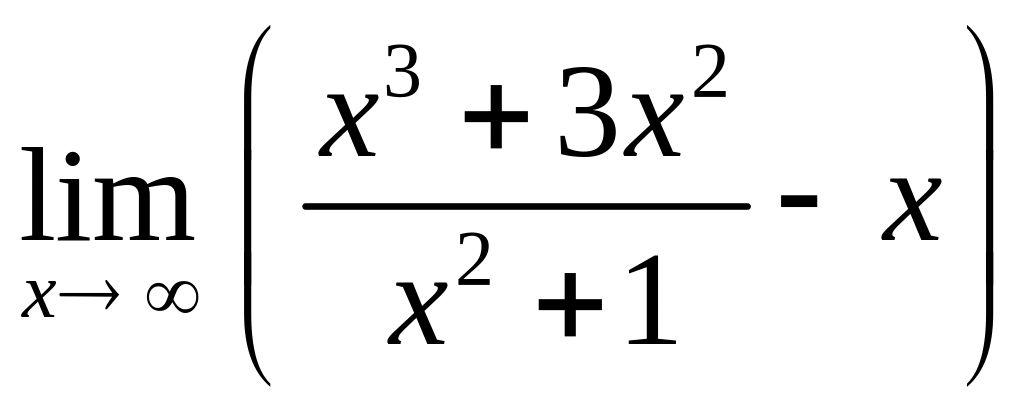 ;
;
3.10.
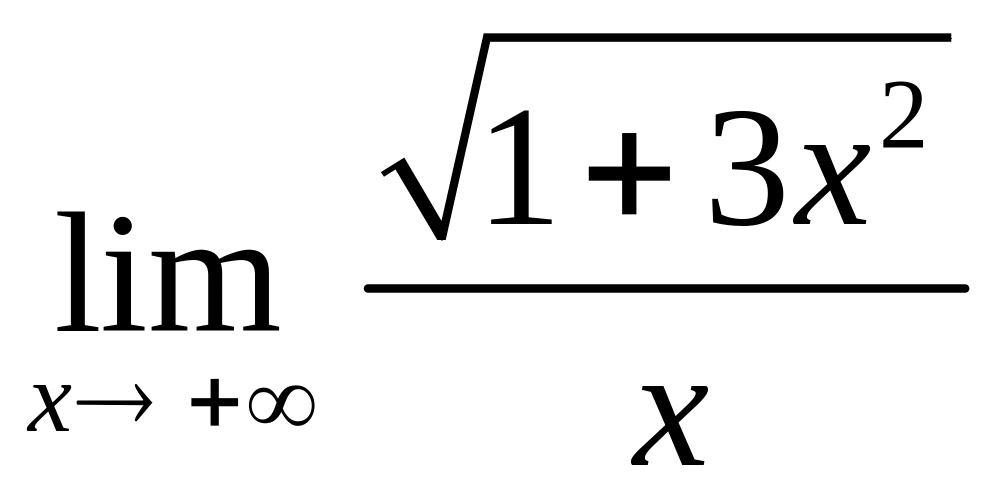 ;
3.11.
;
3.11.
 ;
3.12.
;
3.12.
![]() .
.
4. Задана функция
![]() .
.
Найти односторонние пределы этой
функции в точках
![]() ;
;
Имеет ли эта функция точки разрыва? Если имеет, какого они рода?
5. Написать уравнения асимптот кривой
![]() .
.
Контрольное задание № 1.2
1. Найти область определения функции:
![]() .
.
2. Построить линию:
 .
.
3. Найти пределы функций:
3.1.
![]() ;
3.2.
;
3.2.
 ;
3.3.
;
3.3.
 ;
;
3.4.
 ;
3.5.
;
3.5.
 ;
3.6.
;
3.6.
 ;
;
3.7.
![]() ;
3.8.
;
3.8.
![]() ;
3.9.
;
3.9. ;
;
3.10.
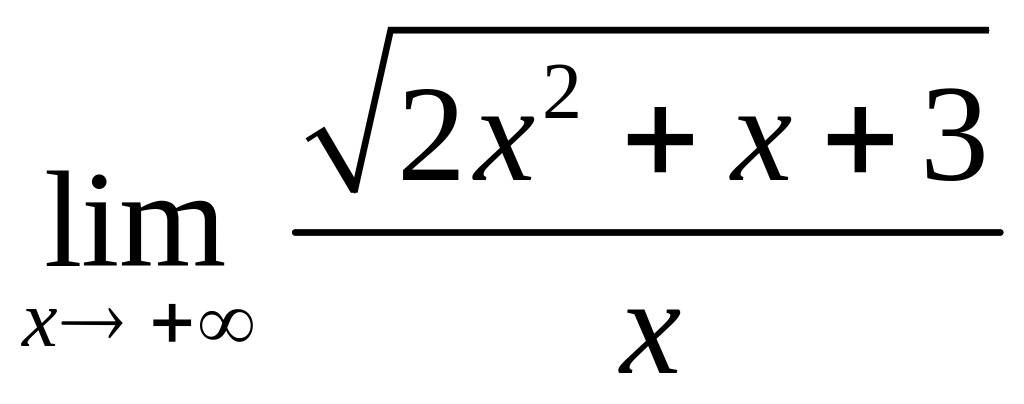 ;
3.11.
;
3.11.
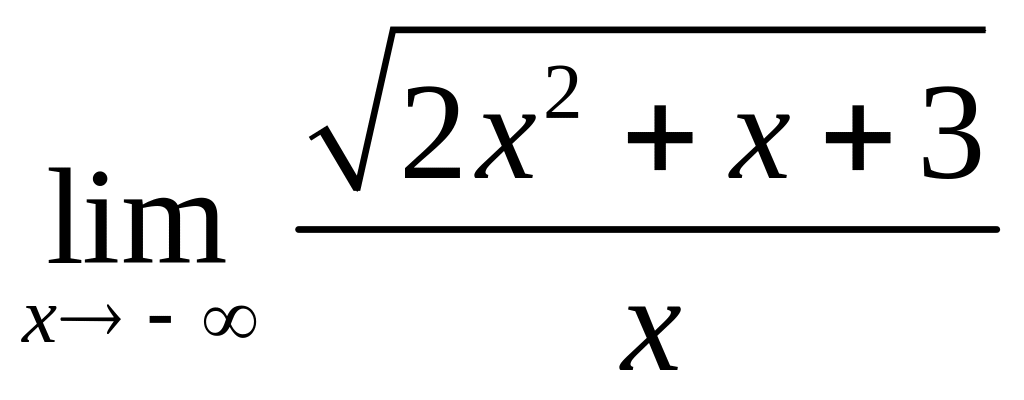 ;
3.12.
;
3.12.
![]() .
.
4. Задана функция
![]() .
.
Найти односторонние пределы этой
функции в точках
![]() ;
;
Имеет ли эта функция точки разрыва? Если имеет, какого они рода?
5. Написать уравнения асимптот кривой
![]() .
.
Контрольное задание № 2.1
1. Найти производные функций:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() .
.
2. Найти дифференциал первого и второго
порядка функции
![]() в т. (1;1).
в т. (1;1).
3. Составить уравнение касательной к
графику функции
![]() в точке
в точке
![]() =0.
=0.
Построить в плоскости
![]() кривую и касательную к ней.
кривую и касательную к ней.
4. Используя дифференциал, найти
приближенное значение
![]() .
.
5. Задана функция
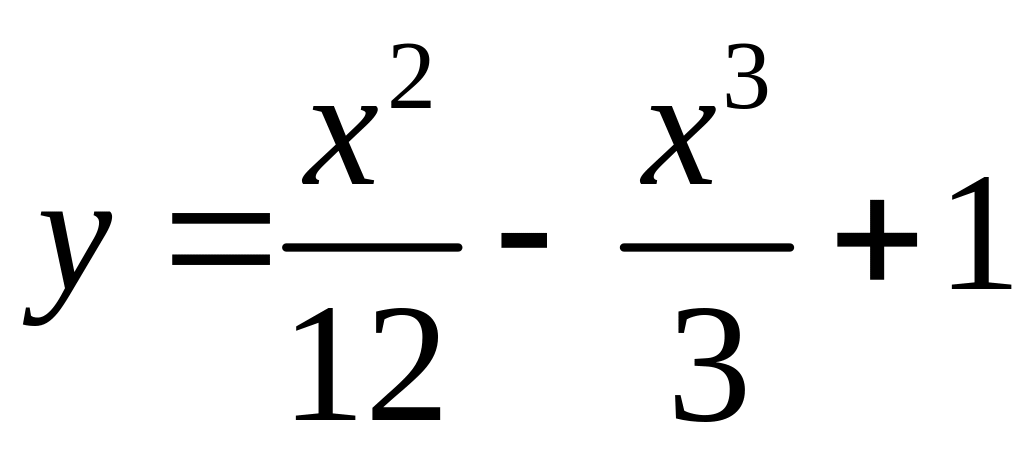 .
.
а) Исследовать функцию на монотонность и экстремумы;
б) Найти наибольшее и наименьшее значения
функции на отрезке
![]() ;
;
в) Найти интервалы выпуклости вверх, выпуклости вниз и точки перегиба функции.
6. Провести полное исследование функции
![]() и построить ее график.
и построить ее график.
Контрольное задание № 2.2
1. Найти производные функций:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() .
.
2. Найти дифференциал 1-го и 2-го порядка
функции
![]() в т. (1;1).
в т. (1;1).
3. Составить уравнение касательной к
графику функции
![]() в точке
=2.
в точке
=2.
Построить в плоскости кривую и касательную к ней.
4. Используя дифференциал, найти
приближенное значение
![]() .
.
5. Задана функция
 .
.
а) Исследовать функцию на монотонность и экстремумы;
б) Найти наибольшее и наименьшее значения функции на отрезке ;
в) Найти интервалы выпуклости вверх, выпуклости вниз и точки перегиба функции.
6. Провести полное исследование функции
![]() и построить ее график.
и построить ее график.
Контрольное задание № 3.1
1. Найти интеграл
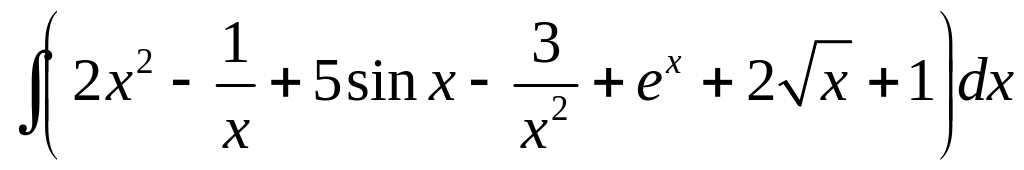
2. Найти интеграл
![]()
3. Найти интеграл
![]() 4. Найти интеграл
4. Найти интеграл
![]()
5. Вычислить

6. Вычислить площадь фигуры, ограниченной линиями:
![]() ;
;
![]() .
.
Решение проиллюстрировать рисунком.
Контрольное задание № 3.2
1. Найти интеграл

2. Найти интеграл
![]()
3. Найти интеграл
 4.
Найти интеграл
4.
Найти интеграл

5. Вычислить

6. Вычислить площадь фигуры,
ограниченной линиями:![]() ;
;
![]() .
.
Решение проиллюстрировать рисунком.
Контрольное задание № 4.1
1. Показать, что функция
![]() является решением дифференциального
уравнения
является решением дифференциального
уравнения
![]() .
.
2. Функция
![]() является решением дифференциального
уравнения
является решением дифференциального
уравнения
![]() .
Построить интегральную кривую этого
уравнения, проходящую через точку
.
Построить интегральную кривую этого
уравнения, проходящую через точку![]() .
.
3. Решить дифференциальное уравнение
![]() .
.
4. Решить дифференциальное уравнение
![]() .
.
5. Решить дифференциальное уравнение
![]() .
.
6. Решить дифференциальное уравнение
![]() .
.
7. Решить дифференциальное уравнение
![]() .
.
8. Найти решение дифференциального
уравнения
![]() ,
удовлетворяющее начальному условию:
,
удовлетворяющее начальному условию:
![]() .
.
Контрольное задание № 4.2
1. Показать, что функция
![]() является решением дифференциального
уравнения
является решением дифференциального
уравнения
![]()
2. Функция
![]() является решением дифференциального
уравнения
является решением дифференциального
уравнения![]() .
Построить интегральную кривую этого
уравнения, проходящую через точку
.
Построить интегральную кривую этого
уравнения, проходящую через точку
![]() .
.
3. Решить дифференциальное уравнение
 .
.
4. Решить дифференциальное уравнение
![]() .
.
5. Решить дифференциальное уравнение
![]() .
.
6. Решить дифференциальное уравнение
![]() .
.
7. Решить дифференциальное уравнение
![]() .
.
8. Найти решение дифференциального
уравнения
![]() ,
удовлетворяющее начальным условиям:
,
удовлетворяющее начальным условиям:
![]() ,
,![]() .
.
Вариант 1
|
Условие: |
1 |
2 |
3 |
4 |
|
1 |
|
1,5 |
2 |
–3 |
–4 |
|
2 |
|
1 |
2 |
–1 |
|
|
3 |
|
0 |
2 |
–1 |
|
|
4 |
|
0 |
0,5 |
2 |
|
|
5 |
|
–0,5 |
1 |
0 |
|
|
6 |
|
0,125 |
0,2 |
0,4 |
0,5 |
|
7 |
|
0 |
0,75 |
3 |
|
|
8 |
|
1 |
е2 |
е–2 |
|
|
9 |
|
3 |
е3 |
е–3 |
|
|
10 |
Односторонние пределы функции
х0=1 равны |
0 и 1 |
0 и 2 |
0 и 0,5 |
1 и 2 |
|
11 |
График функции
имеет асимптоту |
у=4 |
у= 2 |
у=4х–2 |
у=4х+8 |
|
12 |
Найти точки разрыва функции
классифицировать их. Построить эскиз графика. |
|
|
|||
13 |
Вычислить предел:
|
|
|
|||
14 |
Доказать, используя определение:
|
|
|
|||
Вариант 1
|
Условие: |
1 |
2 |
3 |
4 |
|
1 |
|
|
|
|
–7 |
|
2 |
|
|
|
|
|
|
3 |
Производная функции
|
1 |
2е |
3е |
2 |
|
4 |
Производная функции
|
0,2 |
1 |
1,2 |
|
|
5 |
Дифференциал функции
|
4dx |
2dx |
0 |
Не существует |
|
6 |
Уравнение касательной к графику
функции
|
|
|
|
|
|
7 |
Функция
|
|
|
|
|
|
8 |
Максимум функции
достигается в точке
|
–1 |
1/2 |
1 |
–1/3 |
|
9 |
При каком значении а график функции
|
–3 |
3 |
2 |
–5 |
|
10 |
Предел
|
4/3 |
3/4 |
0 |
|
|
11 |
Предел
|
1 |
–4 |
–3 |
5 |
|
12 |
Найти производную функции
|
|
|
|||
13 |
Вычислить
|
|
|
|||
14 |
Исследовать и построить график функции
|
|
|
|||
