
- •Содержание и структура тестовых материалов выходного контроля для 2-х курсов специальности
- •230115 «Программирование в компьютерных системах»
- •Тематическая структура
- •2. Матрицы. Действия над ними
- •4. Аналитическая геометрия на плоскости. Прямая линия, плоскость.
- •5. Линия на плоскости
- •6. Кривые второго порядка
- •7. Линейные операции над векторами
- •8. Длина вектора
- •9. Пределы
- •10. Производная
- •11. Производные высших степеней.
- •12. Применение производной в исследовании функций
- •13. Неопределенный интеграл
- •14. Определенный интеграл
- •15. Геометрическое приложение определенного интеграла.
- •16 .Замена переменной в неопределенном интеграле:
- •17. Частные производные
- •18. Двойные интегралы.
- •19. Дифференциальные уравнения 2-го порядка с постоянными коэффициентами
- •20. Ду высших порядков
- •Ду с разделяющимися переменными
- •22. Ряды
- •23. Знакочередующиеся ряды
- •24. Разложение функции в ряды Тейлора и Маклорена.
- •25. Степень мнимой единицы.
- •26. Действия над комплексными числами
- •27. Тригонометрическая форма комплексного числа
6. Кривые второго порядка
У эллипса большая полуось a равна 3 и малая полуось b равна 2, тогда каноническое уравнение эллипса имеет вид…
![]()
![]()
*![]()
![]()
полуось a равна 4 и малая полуось b равна 3, тогда каноническое уравнение эллипса У эллипса большая имеет вид…
![]()
![]()
*![]()
У гиперболы действительная полуось a равна 3 и мнимая полуось b равна 2, тогда каноническое уравнение гиперболы имеет вид…
*
У гиперболы действительная полуось a равна 2 и мнимая полуось b равна 5, тогда каноническое уравнение гиперболы имеет вид…
*![]()
![]()
![]()
![]()
У гиперболы действительная полуось a равна 4 и мнимая полуось b равна 2, тогда каноническое уравнение гиперболы имеет вид…
![]()
![]()
*![]()
![]()
У гиперболы действительная полуось a равна 3 и мнимая полуось b равна 2, тогда каноническое уравнение гиперболы имеет вид…
*
Парабола задана уравнением х2=-32у. Найдите координаты ее фокуса
(0; -8)
(8;0)
(0;-16)
(-8;0)
Парабола задана уравнением х2=32у. Найдите координаты ее фокуса
(0; -8)
(8;0)
(0;8)
(-8;0)
Парабола задана уравнением у2=-32х. Найдите координаты ее фокуса
(0; -8)
(8;0)
(0;-16)
(-8;0)
Парабола задана уравнением у2=32х. Найдите координаты ее фокуса
(0; -8)
(8;0)
(0;8)
(-8;0)
7. Линейные операции над векторами
Среди векторов
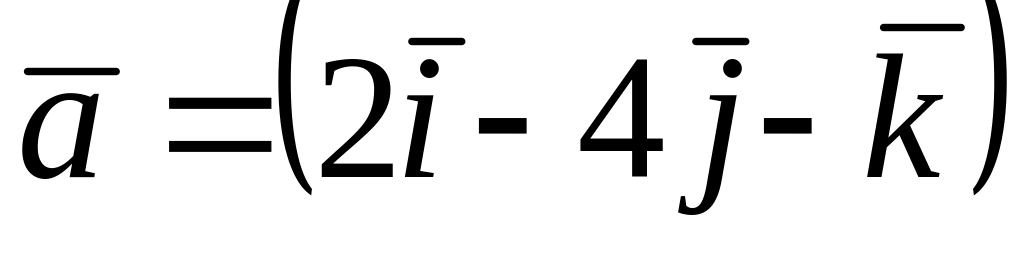 ,
,
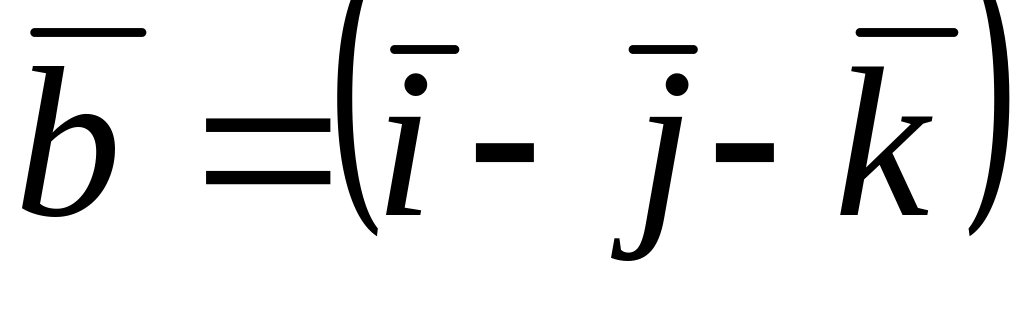
и
![]() коллинеарные…
коллинеарные…
*
![]()
![]()
![]()
![]()
Среди векторов
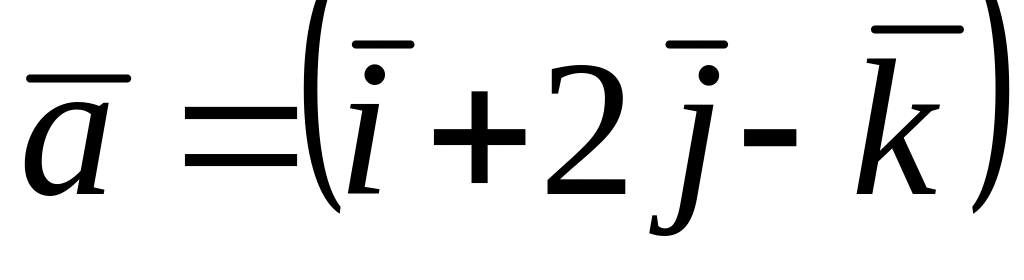 ,
,
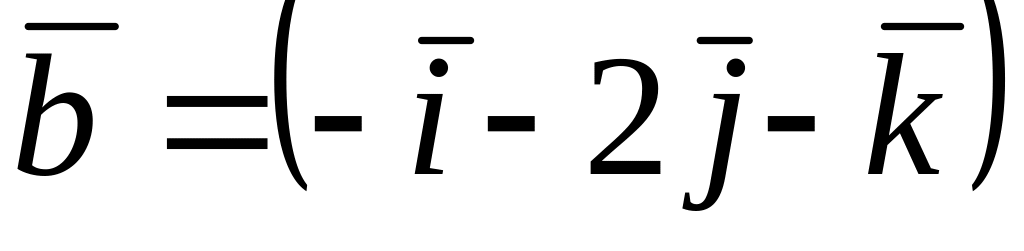
и
![]() коллинеарные…
коллинеарные…
*
![]()
Среди векторов
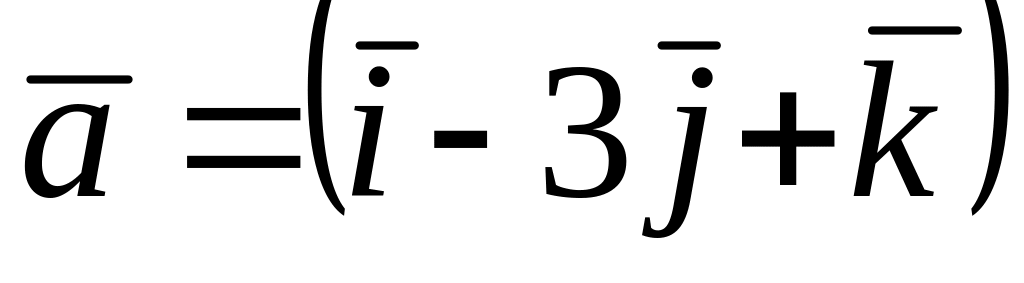 ,
,
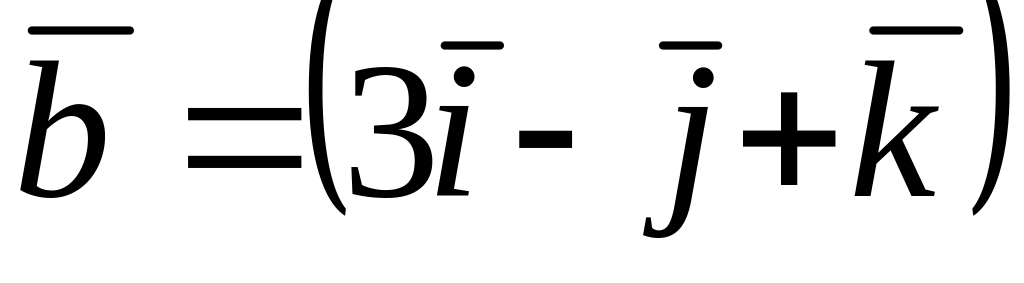
и
![]() коллинеарные…
коллинеарные…
*
Среди векторов
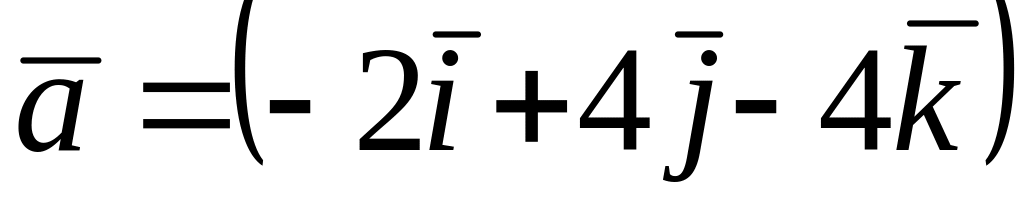 ,
,
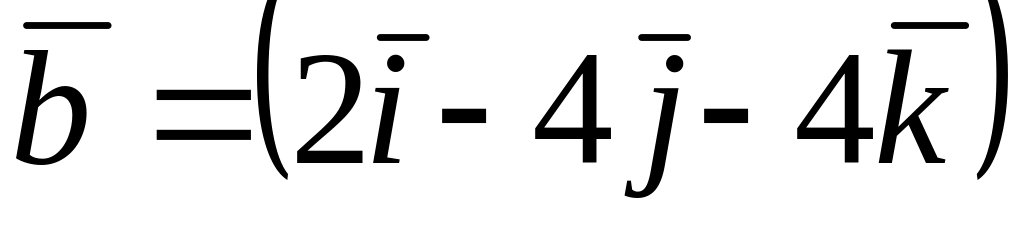
и
![]() коллинеарные…
коллинеарные…
*
Среди векторов
 ,
,
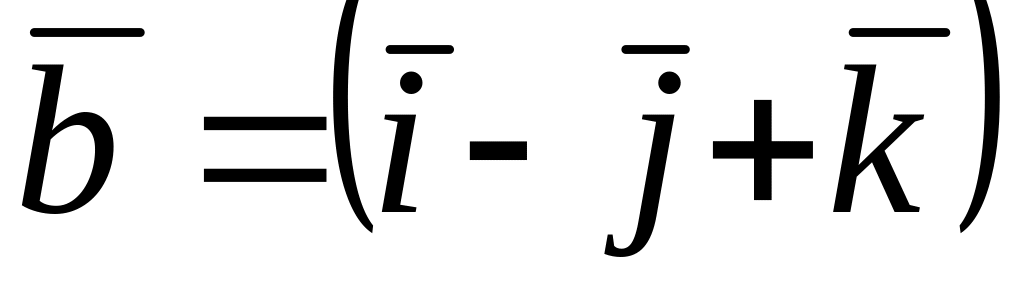
и
![]() коллинеарные…
коллинеарные…
* нет
Среди векторов
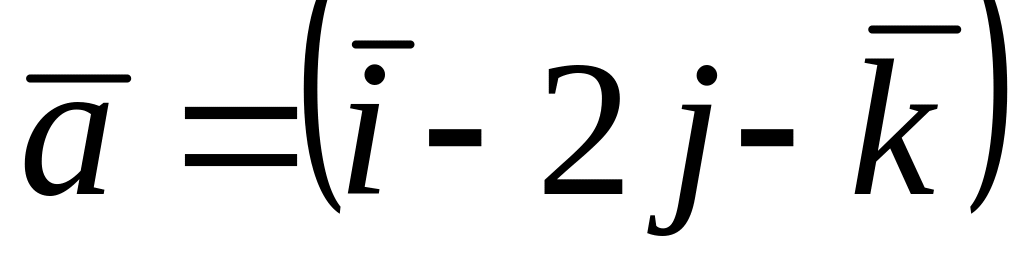 ,
,
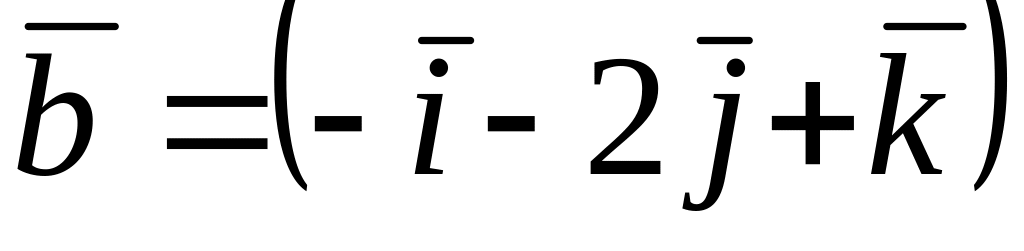
и
![]() коллинеарные…
коллинеарные…
*
Среди векторов
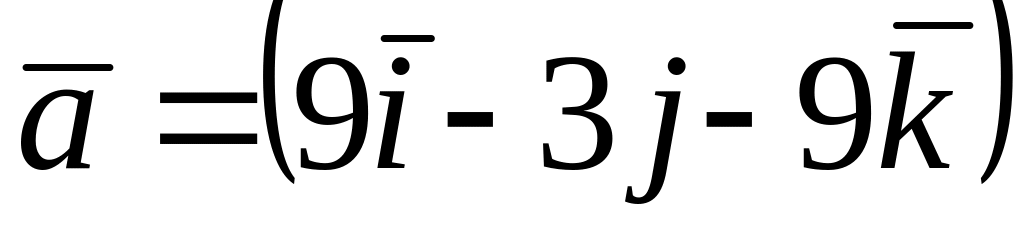 ,
,
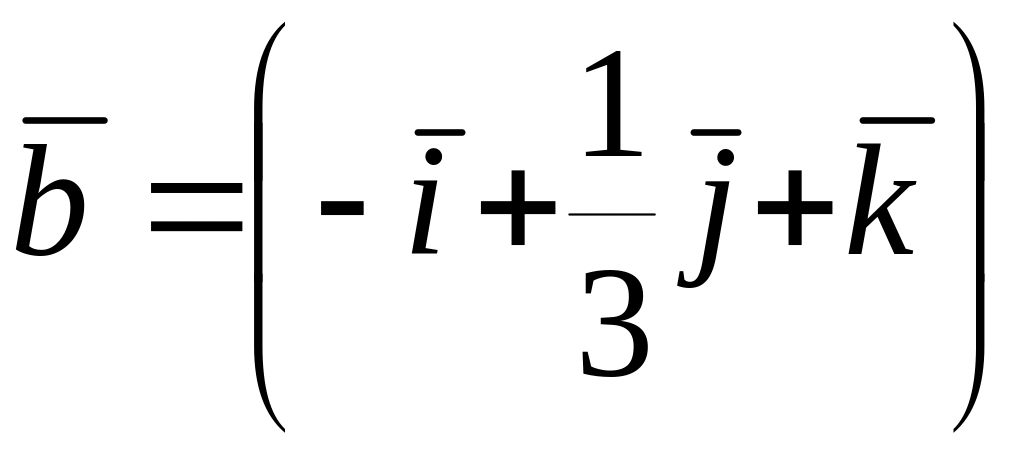
и
![]() коллинеарные…
коллинеарные…
*
Среди векторов
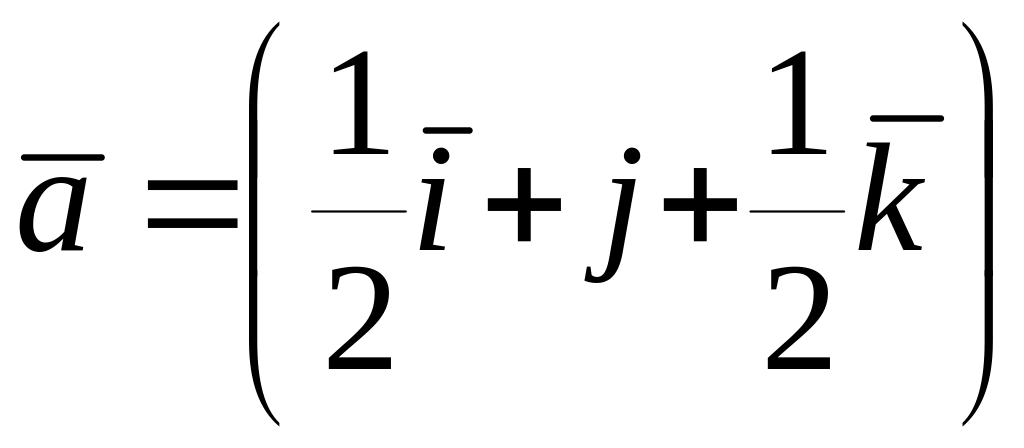 ,
,
и
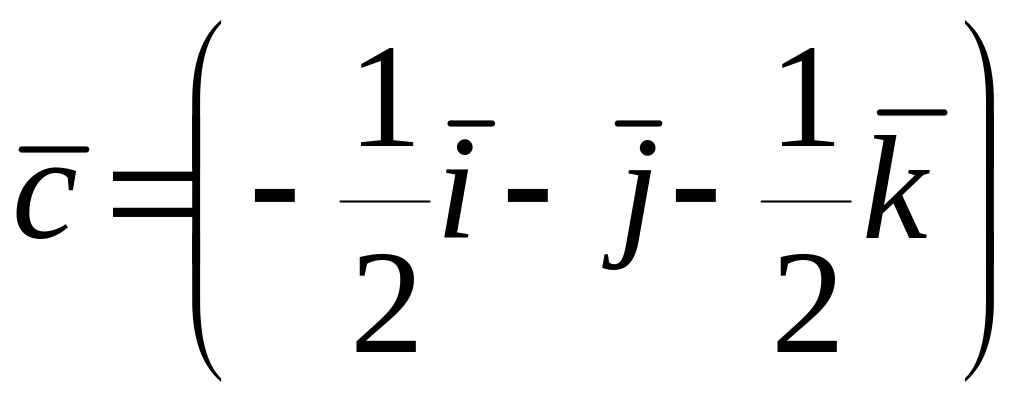 коллинеарные…
коллинеарные…
*
Из векторов
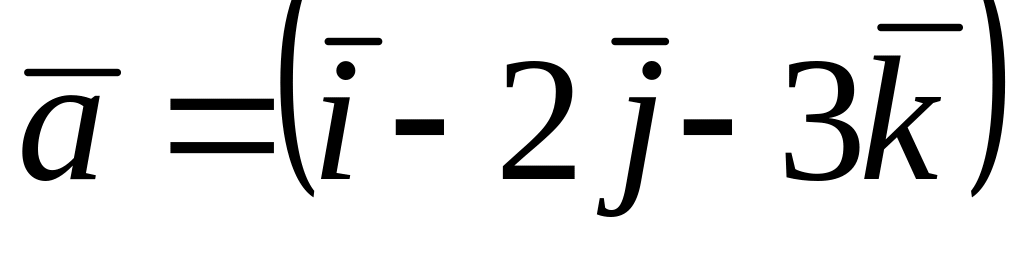 и
и
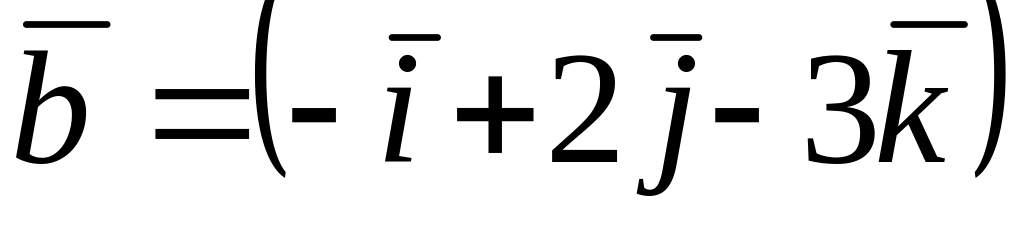 коллинеарные к вектору
коллинеарные к вектору
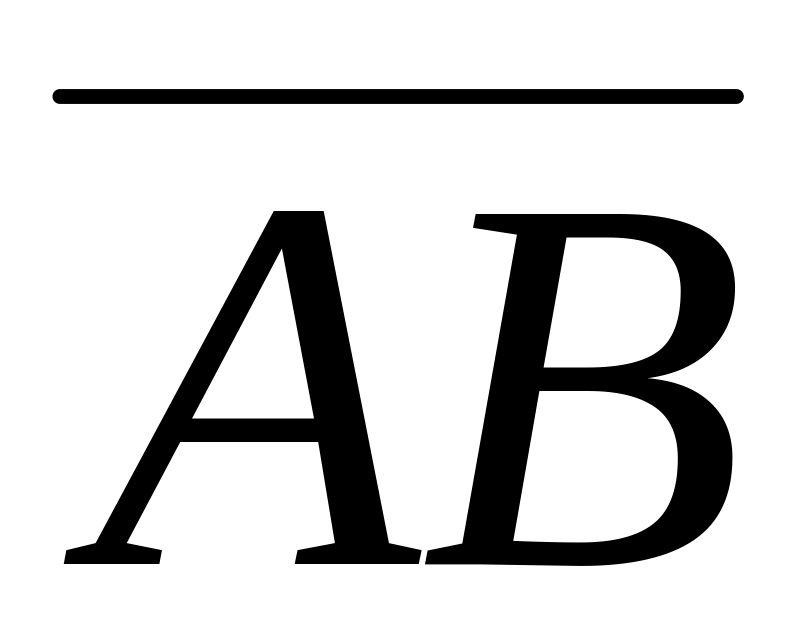 ,
где A=(-3;1;5), B=(-4;3;2)…
,
где A=(-3;1;5), B=(-4;3;2)…
*
![]()
![]()
![]()
нет
Из векторов
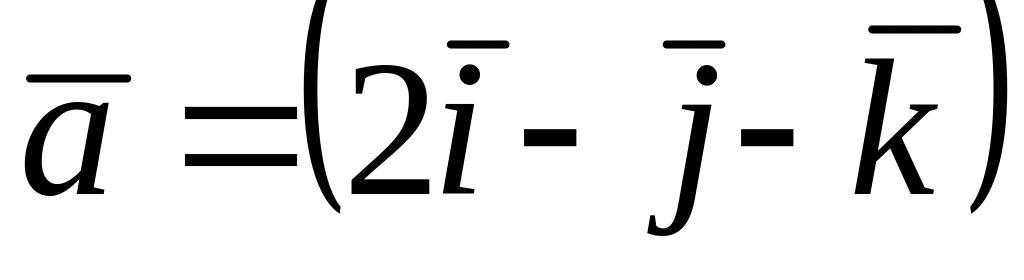 и
и
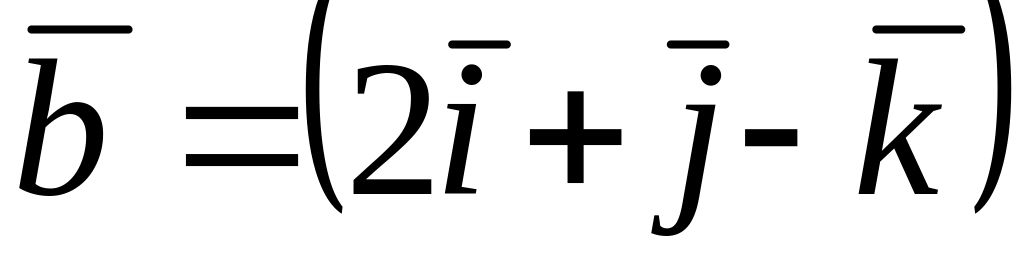 коллинеарные к вектору
,
где A=(-1;2;-1), B=(1;1;-2)…
коллинеарные к вектору
,
где A=(-1;2;-1), B=(1;1;-2)…
нет
*
8. Длина вектора
Вычислить длину вектора
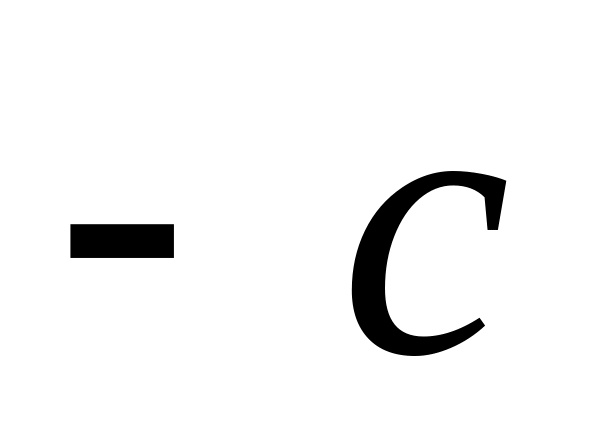 ,
если
,
если
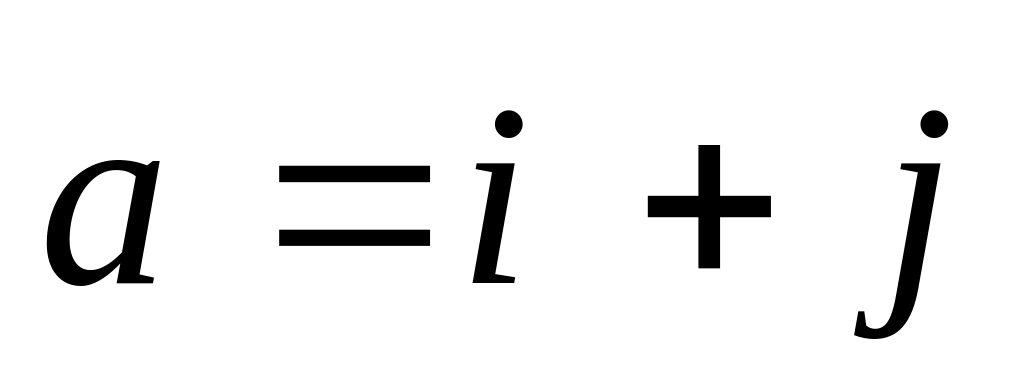 ,
,
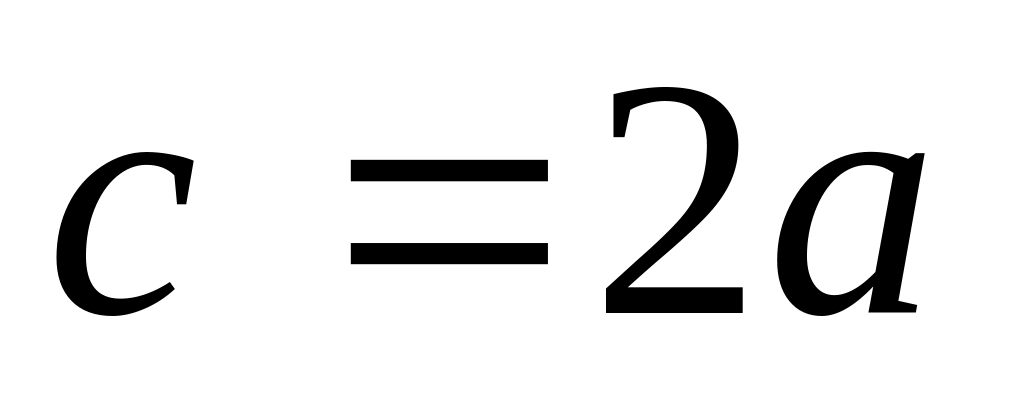
2
4
![]()
*![]()
Вычислить длину вектора , если ,
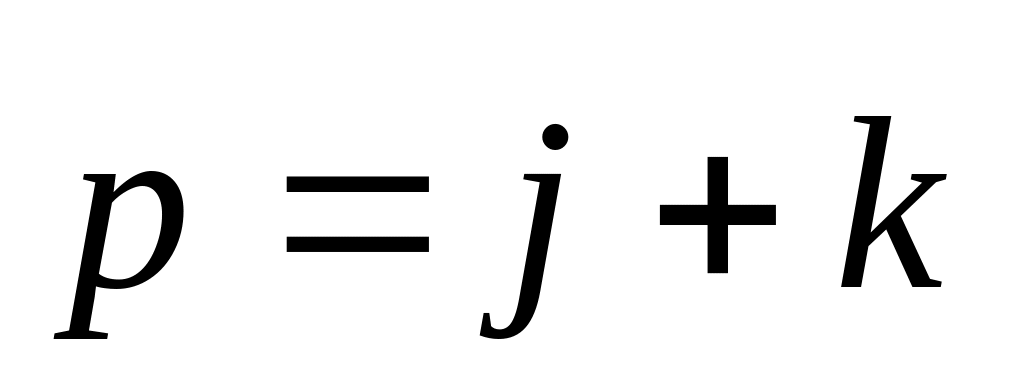 ,
,
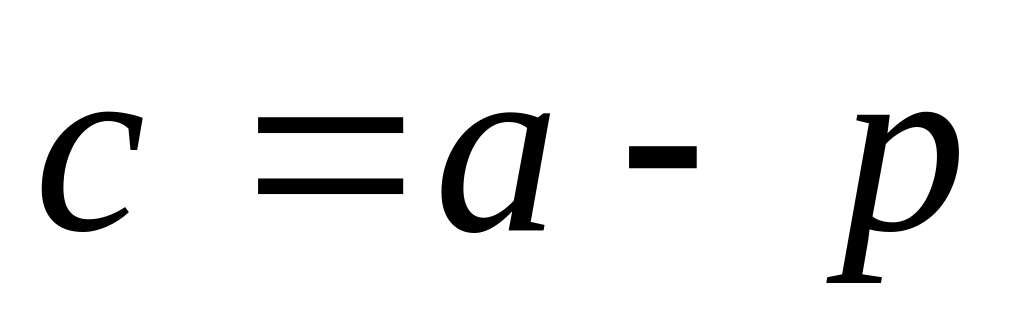
2
4
*
Вычислить длину вектора , если, ,
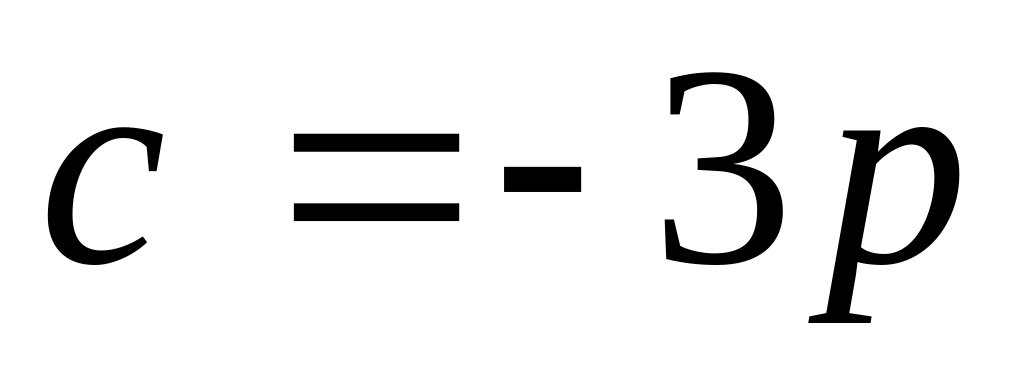
2
4
*![]()
Вычислить длину вектора , если , ,
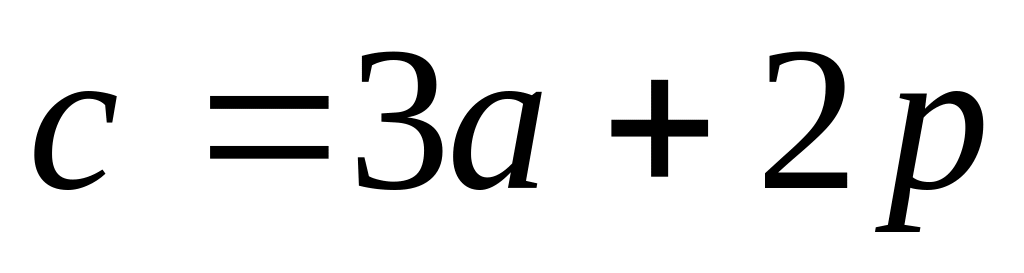
21
*![]()
![]()
5
Сравнить длины векторов
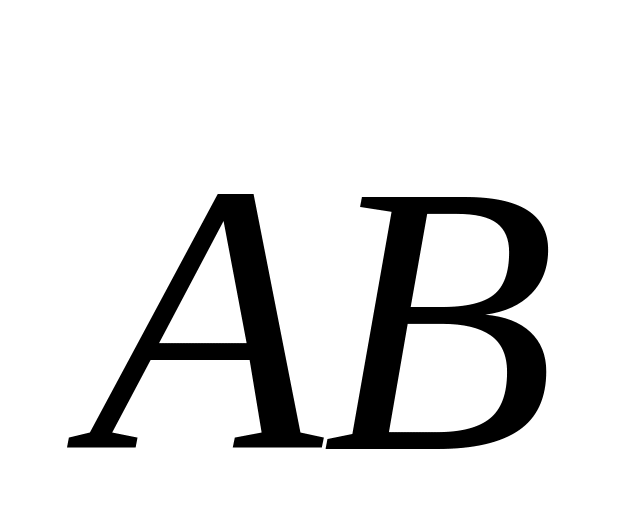 и
и
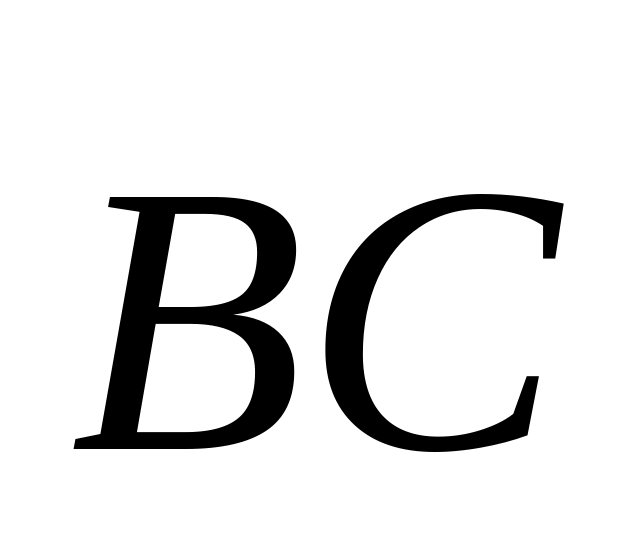 ,
если A(4;0;1), B(0;2;3),
C(2;1;-1)
,
если A(4;0;1), B(0;2;3),
C(2;1;-1)
![]()
*![]()
![]()
Сравнить длины векторов и , если A(2;-1;1), B(1;3;-3), C(0;2;1)
*
Сравнить длины векторов и , если A(1;5;1), B(0;4;-1), C(-2;0;2)
*
Угол между прямыми
х - 2у + 3 = 0 и 3х - у - 5 = 0
равен ... градусам.
45
30
90
0
60
Угол между прямыми
3х + 2у - 6 = 0 и 2х - 3у + 4 = 0
равен ... градусам.
90
45
30
60
0
Угол между прямыми
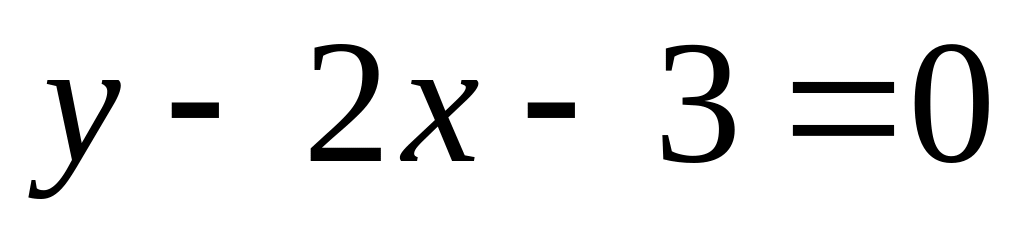 и
и
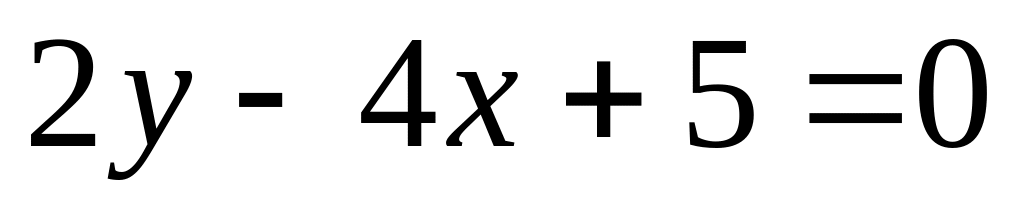 равен:
равен:
![]()
![]()
0
![]()
