4. 1. 2. Переместительное свойство сходящихся рядов
Одним из важнейших свойств суммы конечного числа вещественных слагаемых является переместительное свойство. Естественно возникает вопрос, остается ли справедливым это свойство для суммы сходящегося ряда.
Определение.
Если отображение
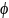является
биекцией
множества
N
натуральных чисел на себя, то ряд
называется
перестановкой
ряда
.
Пример 56. Рассмотрим условно сходящийся ряд:
.
Перестать и сгруппируем члены ряда по три следующим образом:
сумма
которого равна:
.
Таким образом, перестановка членов условно сходящегося ряда изменяет его сумму. В данном случае она уменьшилась вдвое. Рассмотренный пример показывает, что условно сходящийся ряд не обладает переместительным свойством. Полную ясность в вопрос о сходимости перестановки условно сходящегося ряда вносит следующее утверждение.
Теорема 21 (Коши). Если ряд сходится абсолютно, то любая его перестановка также сходится абсолютно, причем к той же сумме.
Рассмотрим
ряд
,
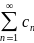общий член которого может быть представлен
в виде
произведения:
.
Приведем
достаточные признаки сходимости
таких
рядов.
Теорема
22 (признак Абеля).
Пусть дан ряд
.
Если последовательность
монотонна
и ограничена, а ряд
сходится, то ряд
сходится.
(Абель Нильс Хенрик(1802–1829) – норвежский математик, один из крупнейших математиков19 века.)
Теорема 23 (признак Дирихле). Пусть дан ряд
1Гармонический ряд – это ряд, каждый член которого, начиная со второго, является средним
гармоническим его соседних
членов: