2. 2. Необходимое условие сходимости ряда

Из критерия Коши сходимости ряда вытекает

Теорема 3. Если ряд суммируем, то предел его общего

члена равен нулю:

(2.3)

Замечание. Как утверждается в теореме, для сходимости ряда необходимо, чтобы Таким образом, если то ряд заведомо расходится.

Наоборот, если 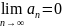, то ряд не обязательно является сходящимся. Пример гармонического ряда показывает, что это условие не является достаточным: ряд расходится, хотя при этом

.

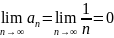Для сходимости ряда недостаточно, чтобы n-й член ряда стремился к нулю; нужно, чтобы он стремился к нулю достаточно быстро (обсуждение этого вопроса в п. 3. 2).

Пример 17. Рассмотрим ряд

(2.4)

составленный из членов геометрической прогрессии: Его

часто называют геометрическим рядом. Исследуем сходимость данного ряда.

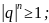Если то следовательно, и в этом случае не выполнен необходимый признак сходимости. Итак, в случае ряд (2. 4) расходится.

Пусть 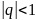. Тогда 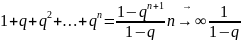, поскольку 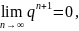если . Значит, ряд в этом случае сходится.

Наоборот, если ряд (2. 4) суммируем, то и, следовательно, .

Таким образом, геометрический ряд суммируем тогда и только тогда, когда , и в этом случае его сумма:

. (2.5)

Пример 18. Ряд расходится, ибо

Пример 19. Ряд 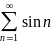расходится, т.к. последовательность не является бесконечно малой. В самом деле, предположим противное: . Тогда . Так как

, то 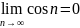, что противоречит равенству . Следовательно, рассматриваемый ряд расходится.

2. 3. Алгебраические операции и сходимость

Теорема 4. Пусть 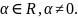Ряды и 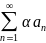одновременно сходятся или расходятся. Если один из них сходится, то

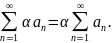
Теорема 5. Два сходящихся ряда можно почленно складывать и вычитать, то есть, если ряды и сходятся, то ряд тоже сходится, причем

.

Следствие. Если два ряда и сходятся, то для любых ряд также сходится и

.

Пример 20. Найдем сумму ряда Данный ряд можно представить как сумму двух рядов: и

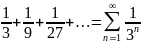. Каждый из них является геометрическим рядом со знаменателем 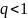, а потому сходится. По формуле (2. 5) суммы первого и второго рядов соответственно равны:

Тогда по теореме 5

Теорема 6. Если ряд сходится, а ряд расходится, то ряд расходится.

Пример 21. Рассмотрим ряд

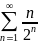Так как и ряд сходится (см. п. 1. 1, пример 14), а гармонический ряд расходится, то ряд 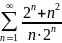расходится.

Теорема 7. Если оба ряда и расходятся, то ряд может как сходиться, так и расходиться.

Пример 22. Рассмотрим ряд .

Так как 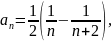то Следовательно, 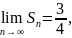т.е. ряд сходится, и его сумма равна В то же время каждый из рядов и является расходящимся. Расходимость второго ряда очевидна: он получается из гармонического отбрасыванием двух его первых членов.