Векторное произведение векторов

В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора. Пусть это будут нетленные буквы  .

Само действие обозначается следующим образом:  . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.

И сразу вопрос: если в скалярном произведении векторов   участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:

Результатом скалярного произведения векторов является ЧИСЛО: 

Результатом векторного произведения векторов является ВЕКТОР:  , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву  .

Определение: Смешанным произведением   некомпланарных векторов  ,взятых в данном порядке, называется объём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис   правый, и знаком «–», если базис   левый.

Смешанное произведение векторов – это произведение трёх векторов

Формула вот = (перемножаете все 3 вектора друг на друга)

Длиной или модулем вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль.

Длина вектора на плоскости вычисляется по следующей формуле:

Длина вектора в трехмерном пространстве вычисляется по следующей формуле:

Формула длины вектора в n-мерном пространстве:

Нахождение угла между векторами, примеры и решения.

Косинус угла между векторами   и  , а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах   и  .

Разберем эти случаи.

По определению скалярное произведение векторов есть 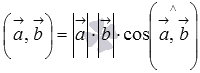 . Если векторы   и   ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов   и  , и мы получим формулу для нахождения косинуса угла между ненулевыми векторами: 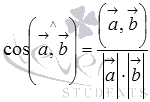 . Эту формулу можно использовать, если известны длины векторов и их скалярное произведение.

Площадь параллелограмма равно произведению основания на его высоту.

Площадь треугольника 1\2 основания на высоту.

Найти объём параллелепипеда, построенного на векторах  ,  ,  .

Решение

Объём параллелепипеда, построенного на векторах  a, b, c численно равен модулю смешанного произведения этих векторов.

 V = | abc |

V = | -7 | = 7

Объем пирамиды

Объем пирамиды равен одной третьей произведения площади основания пирамиды на длину ее высоты: Координаты точки делящие отрезок в заданном соотношении:

1. Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении  , определяются по формулам

Если  , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам