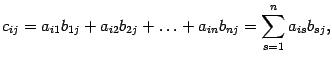Определители и системы линейных алгебраических уравнений

Вычисление определителей основывается на их известных свойствах, которые относятся к определителям всех порядков. Вот эти свойства:

1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.

2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.

3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.

4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число. Для определителей третьего порядка это свойство может быть записано, например, так:

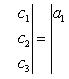
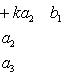
6. Определитель второго порядка вычисляется по формуле

     (1)

7. Определитель третьего порядка вычисляется по формуле

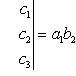
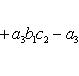
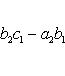
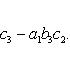     (2)

Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).

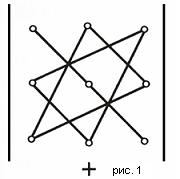
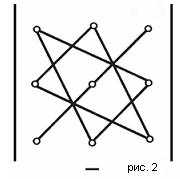
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений.

Алгебраические дополнения 

     Алгебраическое дополнение элемента   определителя   - определитель   где   - минор элемента  .

     Разложение определителя 

     По элементам i-й строки:

     По элементам j-го столбца:

     Например, при n = 4 разложение по первой строке

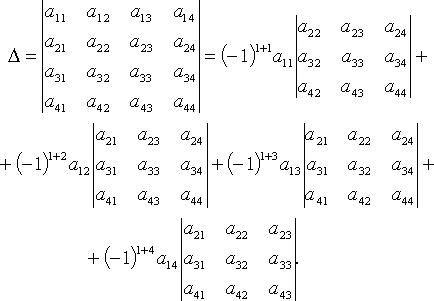
Формулы (метод) Крамера

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А

 = det (a_{i j})

и n вспомогательных определителей  _i (i= ), которые получаются из определителя  заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид:

  x _i =  _i ( i  =  ).                                                (5.4)

Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

x _i =  _i / .

Если главный определитель системы  и все вспомогательные определители  _i = 0 (i=  ), то система имеет бесчисленное множество решений. Если главный определитель системы  = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример 2.14. Решить методом Крамера систему уравнений:

                                               x₁ +   x₂ +  x₃ +      x₄ = 5,

                                               x₁ + 2x₂ -   x₃ +    4x₄ = -2,

                                             2x₁ -  3x₂ -   x₃ -     5x₄ = -2,

                                             3x₁ +   x₂ +2x₃ + 11 x₄ = 0.

Решение. Главный определитель этой системы

 

значит, система имеет единственное решение. Вычислим вспомогательные определители  _i ( i =  ), получающиеся из определителя  путем замены в нем столбца, состоящего из коэффициентов при x_i, столбцом из свободных членов:

              

                  

Отсюда x₁ =  ₁/ = 1, x₂ =  ₂/ = 2, x₃ =  ₃/ = 3, x₄ =  ₄/ = -1, решение системы - вектор С=(1, 2, 3, -1)^T.

Умножение матриц

        Произведением матрицы   размеров   на матрицу   размеров   называется матрица   размеров   , элементы которой вычисляются по формуле

(14.5)

где   ,   .         

Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой -- второй.

Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.

В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.

Правило вычисления элементов произведения можно сформулировать следующим образом.

Для того, чтобы вычислить элемент произведения, стоящий в   -ой строке и   -ом столбце, нужно взять   -ую строку первого сомножителя и   -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить.

Транспонирование матрицы, берешь матрицу, к примеру a11 a22 a 33 (горизонтально написано), и просто переворачиваешь её, то есть записываешь а22 под а11, а а33 под а22 и тд.

Обратная матрица.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Сначала ищем определитель той матрицы которую нам дали, далее находим алгебарические дополнения и миноры, алгебарические дополнения ищутся примерно так:

Если надо найти алгебарическое дополнение а11, закрываешь (мысленно) 1 строку и 1 столбец в матрице, (это можно делать только в матрице 3х3), у тебя должны были остаться а22,а23,а32,а33, далее перемножаешь а22 на а33, и а32 на а23 и из вычитаешь из того, что получилось на месте а22 и а33 а32 и23 ну вот примерно так, предположим у нас числа а22 =5, а23=2, а32=2, а33=2

(5*2) – (2*2) = 6 тут мы получаем алгебарическое дополнение А11=6, ищем минор, если А11 то действуем так, если сумма вот этих 11, 22, 33, дает нам положительное число тогда знак у алгебарического дополнения не меняем, если отрицательное тогда меняем.

Далее переворачиваем матрицу (строка становится столбцом и на оборот), и получившуюся матрицу умножаем по принципу строка на столбец на исходную матрицу.

Находим таким путем С11, С12….С33 записываем все эти получившиеся С в новую матрицу она должна иметь вид единичной, то есть по диагонали с11,с22,с33 должны быть единицы, а все остальные числа нули.