6. Диф. Уравнения высших порядков. Определение общего и частного решений n-го порядка.

уравнение разрешимо относительно т.е. ,

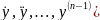
Теорема: Если в уравнении , функция , и её частные производные по переменным , непрерывны в области (n+1)-мерного пространства причём эта область содержит точку с координатами 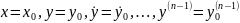– (начальные условия) то в достаточно малом интервале (x₀-h;x₀+h) существует единственное решение y=φ(x) этого уравнение, удовлетворяющее начальным условиям, а задача нахождения

, – Задача Коши.

Общим решением задачи Коши называется функция y=φ(x,C₁,C₂,…,C_n), содержащая n произвольных постоянных если:

• Эта функция при любых значениях постоянных С₁,С₂,…,С_n удовлетворяет уравнению задачи Коши

• Для любых начальных условиях можно подобрать такие значения постоянных, при которых указанная функция удовлетворяет этим начальным условиям

Если общее решение находится в неявном виде т.е. в виде соотношения Ф(x,y,C₁,C₂,…,C_n)=0 то соотношение называют общим интегралом уравнения задачи Коши.

Решение получаемое из общего при конкретных значениях постоянных С₁,С₂,…,С_n , называется частным решением (график его – интегральная кривая уравнения).

7. Диф. Уравнения, допускающие понижение порядка.

Это частные случаи диф. Уравнений 2-го порядка, сводящиеся к решению диф. Уравнения первого порядка.

Рассмотрим некоторые случаи:

1. 

Но _x т.е. можно записать f(x) = _x , отсюда видно что есть первообразная для f(x)

Поэтому +C₁ и общим решением будет y=

2. 

Допустим следовательно и исходное уравнением примет вид

А это есть диф. Уравнение первого порядка для искомой функции z=z(x). Решая его получим z=Ψ(x,C₁) . Отсюда найдём общее решение исходного уравнения y=

3. 

Положим , p – функция от y, но y = φ(x) и из получаем

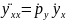
Поэтому . Исходное уравнение примет вид 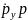=f(y,p), что является диф. Уравнением первого порядка с искомой функцией p=p(y). Решив его, найдём p=Ψ(y,C₁) т.е. или dy=Ψ(y,C₁)dx - уравнение с разделяющимися переменными. Его общий интеграл будет общим решением исходного уравнения

8. Линейные однородные диф. Уравнения второго порядка. Их свойства и теорема о структуре общего решения.

, a₁,a₂ – непрерывные функции от x

• Если y₁=y₁(x) , y₂=y₂(x) – решения уравнения, то y₁+y₂ тоже есть решение этого уравнения.

• Если y₁=y₁(x) – решение уравнения и С – некоторая константа, то Сy₁ тоже является решением этого уравнения

• Если y₁=y₁(x) , y₂=y₂(x) – частные решения уравнения, образующие фундаментальную систему в некотором интервале изменения x, то в этом интервале общее решение уравнения определяется формулой y=C₁y₁(x)+C₂y₂(x)

9. Линейные однородные диф. Уравнения второго порядка с постоянными коэффициентами. Их свойства и теорема о структуре общего решения.

Общее решение будет y=C₁y₁(x)+C₂y₂(x) , y₁(x) и y₂(x) частные решения уравнения, образующие фундаментальную систему в рассматриваемом интервале т.е. задача сводится к их нахождению. Будем искать их виде y=e^kx, , и подставим это в изначальную функцию

В окончательном виде e^kx сокращается и уравнение принимает вид k²+pk+q=0 - характеристическое уравнение. Корни уравнения:

,

Будут три случия:

1. Корни характеристического уравнение действительные и различные т.е.

Общее решение будет иметь вид

2. Корни характеристического уравнения действительны и равны т.е.

Общее решение будет иметь вид

3. Корни характеристического уравнения комплексные т.е.

Тогда k₁=α+iβ , k₂= α-iβ

И общее решение будет y₁=e^αxcosβx+ie^αxsinβx , y₂=e^αxcosβx-ie^αxsinβx