3.3 Полумарковская модель.

Модель процесса чередования структурных состояний ССС в виде полумарковского процесса ПМП более естественно и точно описывает динамику работы реальной системы.

При моделировании полумарковским процессом учитывается возможность изменения переключения структурных состояний ССС в любой текущий момент времени. Полумарковская модель процесса отражает важнейшие статистические характеристики процесса изменения структурных состояний ССС.

Полумарковская модель динамики структурных состояний ССС представляется следующим множеством модельных элементов

где

-пространство структурных состояний. ССС

вектор распределения вероятностей начальных(стартовых)структурных состояний.

матрица переходных вероятностей вложенной в ПМП цепи Маркова,

матрица плотностей вероятностей времени задержек ССС в структурных состояниях,

текущее время работы ССС.

Пример:

3.4 Лазерная измерительная система.

Система имеет два режима работы:

1. Наведение на отражатель (в контролируемую точку),

2. Измерение координат точки.

Число контролируемых точек может достигать нескольких тысяч:

Время наведения луча в точку и время измерения координат представляют собой случайные величины с некоторыми плотностями распределения.

Чередование режимов “наведение-измерение” управляется некоторым вероятностным механизмом (условиями работы).

На рисунках ниже графически иллюстрируется некоторые параметры модели работы системы.

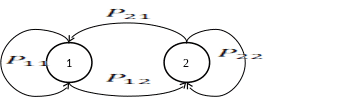
Рис.1 График состояний и переходов модели чередования режимов работы системы.

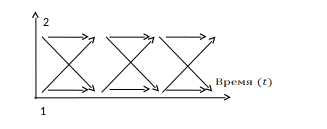Рис.2 Реализация процесса чередования режимов (и структурных состояний системы)

Множество режимов работы (пространство структурных состояний)

Уравнение динамики чередования состояний

Матрица переходных вероятностей.

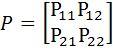
Вектор распределения начальных(стартовых) состояний

Матрица плотностей распределения времен задержек в состояниях

4. Модель динамики технических состояний системы с возможными нарушениями

Для оценки технических состояний многофункциональных систем с возможными нарушениями и восстановлением вводят (ТС)

4.1 Параметры ТС разделяют на

• Основные

• И вспомогательные

В соответствии с тем какие функции системы (основные или вспомогательные) этими параметрами оценивается

4.2 Рассмотрим следующие технические состояния системы:

1. исправное (все проблемы ТС в допусках)

2. работоспособное (все основные параметры ТС в допусках)

3. неработоспособное (хотя бы один из основных параметров вне допуска)

График технических состояний приведен ниже на рисунке

Рис.3 График технических состояний

4.3 Характеристики Марковской модели чередования ТС:

Уравнение динамики чередования состояний:

Матрица переходных вероятностей:

Вектор распределения начальных состояний

Множество возможных состояний

5. Полумарковский процесс

Полумарковские процессы широко используются в теории надежности и теории массового обслуживания. Они объединяют теорию цепей Маркова, разрывных Марковских процессов и теорию восстановления. Приведем сначала определение полумарковского процесса.

Пусть поведение некоторой системы описывается следующим образом. В каждый момент времени система может находиться в одном из возможных фазовых состояний , причем известны начальное состояние системы (в начальный момент она находится в состоянии ) и одношаговые вероятности . Следовательно, процесс есть однородная цепь Маркова.Сопоставим каждому ненулевому элементу матрицы вероятностей перехода случайную величину с функцией распределения . Величине , зависящей как от состояния , так и от состояния , можно придавать разный физический смысл. Она может быть непрерывной или дискретной. В теории надежности и теории массового обслуживания случайную величину обычно рассматривают как время пребывания системы в состоянии при условии, что следующим состоянием, в которое перейдет система, будет . При этом величина считается неотрицательной и непрерывной с плотностью вероятности . При такой интерпретации величину можно назвать временем ожидания в состоянии до перехода в .

Можно себе представить, что точка, отображающая поведение системы на фазовой плоскости, остается в состоянии течение времени , прежде чем она перейдет в . По достижении «мгновенно» (в соответствии с матрицей вероятностей перехода выбирается следующее состояние , и после того как состояние выбрано, время ожидания в полагается равным с функцией распределения или плотностью вероятности . Этот процесс затем следует неограниченно продолжать, выбирая каждый раз независимо следующее состояние и время ожидания. Если через обозначить состояние системы, занятое в момент времени , то полученный случайный процесс принято называть полумарковским.

Из приведенного определения следует, что если игнорировать случайный характер времени ожидания и интересоваться только моментами перехода, то процесс будет представлять собой однородную цепь Маркова. Однако при учете пребывания процесса в разных состояниях в течение случайного отрезка времени процесс не будет удовлетворять уравнению Маркова (если не все времена ожидания распределены экспоненциально). Следовательно, процесс является Марковским только в моменты перехода. Сказанное оправдывает название «полумарковский процесс» или «полумарковская цепь».

При заданном начальном состоянии дальнейшее поведение полумарковского процесса (полумарковской цепи) полностью определяется матрицей вероятностей перехода и матрицей функций распределения или (для непрерывных случайных неличин матрицей плотностей вероятностей