Билет 1

1.Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также при изменении магнитного поля. Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела.

Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия.

В классической физике система уравнений Максвелла описывает взаимодействие электрического поля, магнитного поля и воздействие зарядов на эту систему полей.

Сила Лоренца описывает воздействие электромагнитного поля на частицу.

Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов.

Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Если заряженное тело фиксировано в пространстве, то оно под действием силы не ускоряется. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца).

Для наглядного изображения электрического поля используют силовые линии. Эти линии проводят так, чтобы направление вектора   в каждой точке совпадало с направлением касательной к силовой линии. При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля.

Электрическое поле  положительного заряда.	Электрическое поле  отрицательного заряда

Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы   действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда  :

.

Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном множителе).

В каждой точке пространства в данный момент времени существует свое значение вектора   (вообще говоря - разное в разных точках пространства), таким образом,   - это векторное поле. Формально это выражается в записи

представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к.   может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле, и законы, которым оно подчиняется, есть предмет электродинамики. Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.

Электрический потенциал – это работа, для перемещения заряда 1 Кл из данной точки в точку с нулевым потенциалом, то есть в точку, которая считается началом отсчёта. В электростатике за точку отсчёта обычно принимают бесконечно удалённую точку, в электронике – минусовой вывод источника питания, хотя в принципе точку отсчёта можно выбрать любую, исходя из соображений удобства.  Разность потенциалов – это разность между величинами электрических потенциалов в двух точках независимо от природы того явления, которое создаёт эту разность. Она равна работе по перемещению заряда 1 Кл из одной точки в другую.

ЭДС – это характеристика источника электрической энергии (гальванического элемента, батареи, генератора). Она численно равна разности потенциалов между плюсовым и минусовым выводами источника питания на холостом ходу, то есть при отсутствии тока. Например, когда батарейка не включена в электрическую цепь. 

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:   

 

 - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.

Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.

За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.

Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.

В СИ потенциал измеряется в вольтах: 

  

 

Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.

Токи электрического смещения в пустоте возникают при изменении электрического поля во времени и также окружены магнитным полем. Следовательно, при всяком изменении электрического поля во времени возникает в том же пространстве связанное с ним магнитное поле. Оба эти поля определяют и в этом случае единое электромагнитное поле.

Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды.

Учитывают поляризацию с помощью вектора поляризации  , который для анизотропных и однородных сред выражается через напряженность поля следующим образом:  , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = s_связ ).

Кроме этого, при анализе электростатических полей используют вектор электрического смещения:

	→ D= ε0 ·

→ E

D	вектор электрического смещения,	Кулон/метр2
E	напряженность электрического поля,	Вольт/метр
ε0	электрическая постоянная, 8.85·10-12	Кулон/(Вольт · метр)

ТОК СМЕЩЕ́НИЯ, величина, пропорциональная скорости изменения переменного электрического поля в диэлектрике или вакууме. Название «ток» связано с тем, что ток смещения, так же как и ток проводимости, порождает магнитное поле. Выразим плотность j_см тока смещения через характеристики электрического поля. Для этого найдем плотность j_пртока проводимости в сечении пластин

                         j_пр =  ,                 (4.5)          

где S – площадь пластин, q – их заряд, σ – поверхностная плотность заряда. Из постулированной непрерывности тока во всей цепи следует, что j_см = j_пр, то есть

                         j_см =                              (4.6)     

Плотность заряда σ связана с напряженностью поля в конденсаторе формулой (1.22)

                         σ = Е/ε₀

В данном рассмотрении удобнее характеризовать электрическое поле не вектором напряженности Е, а вектором электрической индукции D. Согласно (1.64) для вакуума D = ε₀Е, поэтому σ = D. Тогда из (4.6) получаем

                         j_см = 

В общем случае электрическое поле является функцией координат и времени, поэтому в последнем выражении следует использовать символ частной производной по времени:

                         j_см =                              (4.7)

Таким образом,  плотность тока смещения равна скорости изменения электрической индукции. Ток смещения, естественно, не переносит зарядов. Из всех физических свойств электрического тока Максвелл приписал току смещения лишь одно свойство – способность создавать в окружающем пространстве магнитное поле. Если взять любой контур L, пронизываемый током смещения I_см , то напряженность магнитного поля связана  с током смещения теоремой о циркуляции вектора Н по замкнутому контуру L:

                                                       (4.8)

При этом сила тока смещения I_см находится через плотность тока j_см путем интегрирования плотности тока по всей площади S контура L.

                                             (4.9)

где   - нормальная составляющая вектора  . Объединяя (4.8) и (4.9), получаем

                                                 (4.10)

Если помимо тока смещения контур  L  пронизывают токи проводимости, их необходимо учесть при интегрировании в правой части (4.10). В результате уравнение (4.10) примет вид:

                                            (4.11)

Соотношения (4.4) и (4.11) представляют собой два основополагающих уравнения теории Максвелла.

Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает

Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно, 

Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна 

C учетом соотношения  можно записать 

В изотропном диэлектрике направления векторов D и E совпадают и  Подставим выражение  , получим 

Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика.

Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов q_i на величину dr_i, составляет 

Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно,  . Вектор P связан с вектором E соотношением  . Подставив это выражение в формулу для работы, получим

Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика

.

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:

Билет 2

1. Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В системе СИ ёмкость измеряется в фарадах. [ф]

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводникибесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

 где   — заряд,   — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ):

где ε₀ — электрическая постоянная, ε — относительная диэлектрическая проницаемость.

Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом – к конденсатору

В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

где S — площадь одной бкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость реды между обкладками, ε₀ = 8.854·10⁻¹² Ф/м — электрическая постоянная.

2.Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.

Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.

Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.

Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита

Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.

Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается, что связано с увеличением тепловой скорости движения носителей заряда и, соответственно, снижению требований для образования электрического пробоя.

Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя.

3.Плоский конденсатор. Две плоские параллельные пластины одинаковой площадиS, расположенные на расстоянии d друг от друга, образуют плоский конденсатор. Если пространство между пластинами заполнено средой с относительной диэлектрической проницаемостью  , то при сообщении им заряда q напряженность электрического поля между пластинами равна , разность потенциалов равна  . Таким образом, емкость плоского конденсатора .

- емкость конденсатора (С). Если его пластины образуют параллельные плоскости, то его называют плоским.

4.  - емкость плоского конденсатора. Зависит от площади его пластин S; от расстояния между его пластинами d; от материала, заполняющего пространство между пластинами ε. При изготовлении конденсатора большой емкости стремятся сделать большое S при малом d, а также заполнить его пространство веществами с большим ε. Не зависит от напряжения U и от заряда q.

Билет 3

1. Параллельное соединение конденсаторов

На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U, Q2 = C2U, Q3 = C3U, а заряд, полученный от источника Q = Q1 + Q2 + Q3.

Рис. 1. Схема параллельного соединения конденсаторов

Общая емкость равнозначного (эквивалентного) конденсатора:

C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,

т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны:Q1 = Q2 = Q3 = Q

Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды. 

Рис. 3. Схема последовательного соединения конденсаторов

Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.

Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей. 

При смешанном соединении конденсаторов для участков с параллельным соединением применяются свойства параллельного соединения конденсаторов, а для участков с последовательным соединением - все свойства последовательного соединения конденсаторов.

Всякое смешанное соединение конденсаторов путем упрощений может быть сведено либо к параллельному соединению, либо к последовательному.

Пример1

 

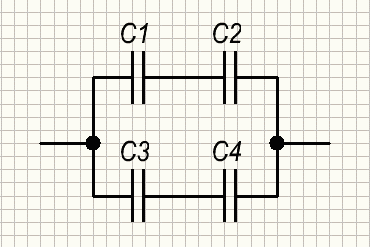
  Эквивалентная емкость верхней ветви

 

  Эквивалентная емкость нижней цепи

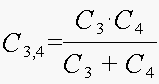
 Теперь это смешанное соединение конденсаторов может быть приведено к параллельному соединению. Эквивалентная емкость всей батареи конденсаторов

 

2.Эквивалентная емкость(равнозначная) равна сумме емкостей.

Найти эквивалентную емкость - это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов. Рассчитывается по тем же формулам

Билет 4

1. Постоя́нный ток — электрический ток, параметры, свойства, и направление которого не изменяются (в различных смыслах) со временем.

Простейшим источником постоянного тока является химический источник (гальванический элемент или аккумулятор), поскольку полярность такого источника не может самопроизвольно измениться.

Для получения постоянного тока используют также электрические машины — генераторы постоянного тока.

В электронной аппаратуре, питающейся от сети переменного тока, для получения постоянного тока используют выпрямитель. Далее для уменьшения пульсаций может быть использован сглаживающий фильтр и, при необходимости, стабилизатор тока или стабилизатор напряжения.

2.Электрическая цепь это совокупность устройств, соединенных определенным образом, которые обеспечивают путь для протекания электрического тока.

Элементами электрической цепи являются: источник тока, нагрузка и проводники. Простейшая электрическая цепь показана на рисунке 1.

Рисунок 1. Простейшая электрическая цепь.

В состав электрической цепи могут входить и другие элементы, таки как устройства коммутации, устройства защиты.

Как известно, для возникновения тока необходимо соединить две точки, одна из которых имеет избыток электронов в сравнении с другой. Другими словами необходимо создать разность потенциалов между этими двумя точками. Как раз для создания разности потенциалов в цепи применяется источник тока.Источником тока в электрической цепи могут быть такие устройства, как генераторы, батареи, химические элементы и т.д.

Нагрузкой в электрической цепи считается любой потребитель электрической энергии. Нагрузка оказывает сопротивление электрическому току и от величины сопротивления нагрузки зависит величина тока. Ток от источника тока к нагрузке течет по проводникам. В качестве проводников стараются использовать материалы с наименьшим сопротивлением (медь, серебро, золото).

Если через поперечное сечение проводника проходит Q кулонов электричества за t секунд, то количество электричества, прошедшего через поперечное сечение проводника в течение одной секунды, называется величиной тока и обозначается буквой I.

Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности тока и всюду ортогональности ее плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:

где I - сила тока через поперечное сечение проводника площадью S

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источникахпостоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительногозаряда вдоль контура.

ЭДС – это характеристика источника электрической энергии (гальванического элемента, батареи, генератора). Она численно равна разности потенциалов между плюсовым и минусовым выводами источника питания на холостом ходу, то есть при отсутствии тока. Например, когда батарейка не включена в электрическую цепь. 

ЭДС можно выразить через напряжённость электрического поля сторонних сил ( ). В замкнутом контуре ( ) тогда ЭДС будет равна:

, где   — элемент длины контура.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождениюэлектрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса (комплексное сопротивление, полное сопротивление) и волнового сопротивления. Сопротивлением(резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

где

R — сопротивление;

U — разность электрических потенциалов на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

Электри́ческая проводи́мость (электропроводность, проводимость) — способность тела проводить электрический ток, а также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению.

Билет 5

 закон Ома для полной цепи. Следует иметь ввиду: - полная цепь должна включать в себя всю цепь целиком вместе с источником тока ε; - под силой тока I следует иметь ввиду исключительно общий ток во всей цепи (правильнее было бы писать I₀); - под сопротивлением R следует иметь исключительно общее сопротивление всей цепи (правильнее было бы писать R₀); - по этой формуле нельзя рассчитывать отдельные участки цепи; для этого наряду с законом Ома для полной цепи пользуются законом Ома для участка цепи. - сила тока короткого замыкания источника тока (когда R = 0). U = ε - напряжение и ЭДС имеют одинаковое значение при разомкнутой цепи (R = ∞; I = 0)

- закон Ома для участка цепи. Это главный закон при расчете электрической цепи. Следует иметь ввиду: - сила тока I - величина зависимая от независимых напряжения U и сопротивления R.

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.  Формула:  A= U*I*t  1 Джоуль = 1 Вольт * 1 Ампер * 1 секунда  Мощность электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока.  Формула:  P=UI  1 Ватт = 1 Вольт * 1 Ампер

Условие получения максимальной мощности во внешней цепи

Максимальная мощность во внешней цепи выделяется когда сопротивление внешней цепи равно внутреннему сопротивлению источника.

Билет 6

Двухполюсник – это электрическая цепь, имеющая два выхода. Двухполюсники, содержащие источники электрической энергии, называют активными, а без таких источников – пассивными.

а

Б

Эквивалентная схема двухполюсника: а – пассивного, б – активного

6. Различают двухполюсные и многополюсные (трехполюсные, четырехполюсные и т. д.) элементы цепи. Двухполюсные элементы имеют два зажима; к ним относятся источники энергии (за исключением многофазных и управляемых источников), резисторы, конденсаторы, индуктивные катушки.Наиболее распространенные трехполюсные элементы — это электронные лампы (вакуумные триоды) и транзисторы (полупроводниковые триоды). 4Примерами четырехполюсных элементов могут служить трансформаторы, индуктивные катушки с подмагничиванием (дроссели с подмагничиванием), интегральные операционные усилители.

Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источников электрической энергии, — пассивными. Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной — сопротивлением r(входное). Поэтому на эквивалентной схеме пассивный двухполюсник может быть представлен одним резистивным элементом с сопротивлением rвх, называемым входным сопротивлением пассивного двухполюсника.

Если известна схема пассивного двухполюсника, то для определения входного сопротивления rВХ нужно тем или иным способом ее «свернуть» относительно двух заданных выводов.

Рассмотрим, например, схему на рис. 5.9, а. Если выделить в этой схеме ветвь с источником ЭДС Е1 к сопротивлением r1 то остальную часть схемы (обведенную штриховой линией) можно рассматривать относительно выводов 1-1' как пассивный двухполюсник (без источников энергии). Часть той же схемы относительно выводов 2-2' ветви с сопротивлением r2 (рис. 5.9, б) можно рассматривать как активный двухполюсник (обведен штриховой линией).

Если в электрической цепи выделено более двух выводов, то соответствующий участок цепи называется многополюсником, например с четырьмя или двумя парами выводов - четырехполюсник.

Активная ветвь, названная так из-за наличия источника ЭДС, изображена на рис. 2.2. Между выходными зажимами ветви возникает напряжение Uаb. Индексация показывает направление ко второму индексу. Напряжение - это разность потенциалов между двумя точками, т. е. Uab =Va-Vb. Определим потенциал точки а, исходя из потенциала Vb. Рассчитаем

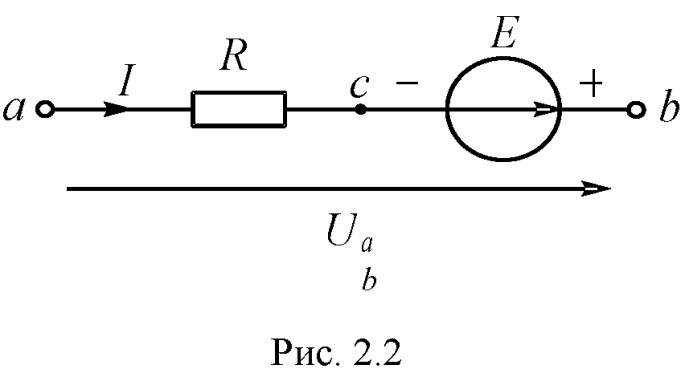
изменение потенциала промежуточной точки с (см. рис. 2.2) по сравнению с Vb. Между точками b и с расположен источник ЭДС, поэтому потенциал точки с отличается от потенциала точки b на величину Е. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с ниже потенциала точки b. Между точками с и а находится резистор сопротивлением R. Потенциал Va отличается от потенциала Vc величиной напряжения на резисторе RI. Ток направлен от большего потенциала к меньшему, поэтому потенциал Va выше потенциала Vc Таким образом,

можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса напряжения к первому. Решим уравнение относительно тока:

Это выражение называют законом Ома для активной ветви. Последнее выражение можно составить, исходя из следующих рассуждений. Для появления тока в ветви есть два условия: наличие разности потенциалов между концами ветви и действие источника ЭДС.

Если направления ЭДС и напряжения Uаb совпадают с направлением тока, они  способствуют его появлению и должны быть записаны в уравнение со знаком плюс. В противном случае - со знаком минус. Рассуждая таким образом, получим для тока ветви прежнее выражение.

на активном участке цепи J=U/R, сила тока J на участке цепи пропорциональна падению напряжения на этом участке U и обратнопропорциональна активному сопротивлению участка R. анологично на пассивном участке J=U/X, где Х реактивное сопротивление, равное векторной сумме емкостного и индуктивного сопротивлений X=Xл-Хс, и Хл=wL, Xc=1/wC, w - циклическая частота. для всей цепи Z=U/((R^2+(Xл-Xc)^2)^1/2.

Билет 7

Четырёхпо́люсник — многополюсник, имеющий четыре точки подключения. Как правило, две точки являются входом, две другие — выходом.

Схема четырёхполюсника

При анализе электрических цепей очень часто бывает удобным выделить фрагмент цепи, имеющий две пары зажимов. Поскольку электрические (электронные) цепи очень часто связаны с передачей энергии или обработкой и преобразованием информации, одну пару зажимов обычно называют «входными», а вторую — «выходными». На входные зажимы подаётся исходный сигнал, с выходных снимается преобразованный.

Такими четырёхполюсниками являются, например, трансформаторы, усилители, фильтры, стабилизаторы напряжения, телефонные линии, линии электропередачи и т. д.

Однако математическая теория четырёхполюсников не предполагает никаких преопределённых потоков энергии/информации в цепях, поэтому названия «входные» и «выходные» являются данью традиции и с этой оговоркой будут использоваться далее.

Состояния входных и выходных зажимов определяются четырьмя параметрами: напряжением и током во входной (U₁, I₁) и выходной (U₂, I₂) цепях. В этой системе параметров линейный четырёхполюсник описывается системой из двух линейных уравнений, причём два из четырёх параметров состояния являются исходными, а два остальные — определяемыми. Для нелинейных четырёхполюсников зависимость может носить более сложный характер. Например, выходные параметры через входные можно выразить системой

К входу четырехполюсника (1-1) подсоединен источник электрической энергии с задающим напряжением Uг и внутренним сопротивлением Zг. К выходным зажимам (2-2) присоединена нагрузка с сопротивлением Zн. На входных зажимах действует напряжение U1, на выходных - U2. Через входные зажимы протекает ток I1, через выходные - I2.

Четырехполюсники бывают пассивными и активными. Пассивные схемы не содержат источников электрической энергии, активные – содержат.

Тип	Система уравнений	Эквивалентная схема	Измерение параметров

Определение параметров четырехполюсников – ДОДЕЛАТЬ111

Схемы замещения четырехполюсника

Так как четырехполюсник характеризуется тремя независимыми коэффициентами, то из этого следует, что его простейшая схема замещения должна содержать три независимые элементы. Существует две такие схемы: а) Т- образная схема или схема звезды, б) П-образная схема или схема треугольника (рис. 159а, б).

Установим соотношения между коэффициентами четырехполюсника A, B, C, D и параметрами элементов схем замещения.

 На основании законов Кирхгофа получим для Т-образной схемы (рис. 1а):

Сравнивая полученные выражениями с уравнениями четырехполюсника формы А, находим нужные соотношения:

На основании законов Кирхгофа получим для П-образной схемы (рис. 1б):

  Сравнивая полученные выражения с уравнениями четырехполюсника формы А, находим нужные соотношения:

 

Для семитричного четырехполюсника должны выполняться равенства: - для Т-образной схемы и  - для П-образной схемы.

Переход от Т-образной схемы к П-образной и наоборот выполняется по известным формулам преобразования схемы звезды в схему треугольника и наоборот.

Частотные характеристики четырехполюсников – ДОДЕЛАТЬ111

Билет 8

Независимый источник напряжения обеспечивает заданное значение напряжения на его полюсах независимо от того,какой ток (в любом направлении) течет через него. Теоретически он поддерживает это напряжение даже при коротком замыкании его полюсов. Хотя создать идеальный источник напряжения невозможно. Можно легко представить реальный источник в виде комбинации резисторов или каких-либо иных элементов с идеальным источником. Характеристика источника напряжения на плоскости i - и показана на рис. 1.2.1,б. сравнивая эту характеристику с вольт-амперной характеристикой резистора, можно видеть, что независимый источник напряжения ведет себя как специфический нелинейный резистор. Если напряжение меняется. то эта прямая линия поднимается или опускается. Особым является случай, когда напряжение источника тождественно равно нулю. При этом характеристика совпадает с осью абсциссх и через источник может течь любой ток, хотя никакого напряжения на его полюсах не возникает. Отсюда заключаем, что идеальный источник напряжения при е=0 ведет себя как короткозамкнутая цепь.

Рис.1.2.1.Обозначения и характеристики независимых источников напряжения (а,б) и тока (в,г)

Напряжение на его полюсах зависит от цепи, подключенной к источнику. Теоретически идеальный источник тока будет создавать заданный ток даже в разомкнутой цепи, что возможно только в предположении бесконечно большого напряжения между его полюсами. Этот элемент является идеализированным, но в комбинации с другими элементами он может быть использован для моделирования реальных источников. Характеристикой источника тока является вертикальная линия на плоскости i - и, как это показано на рис. 1.2.1, г. При различных значениях тока источника эта линия сдвигается влево или вправо. Если ток равен нулю, то характеристика совпадает с вертикальной осью u и ток равен нулю независимо от приложенного напряжения. Отсюда заключаем, что идеальный источник тока при i = 0 эквивалентен разомкнутой цепи.

Зависимые

Первые четыре типа четырехполюсников, которые рассматриваются, это зависимые источники. Они содержат идеальный источник тока или напряжения, такой же, как и независимый источник, описанный ранее. Отличие состоит лишь в том, что напряжение или ток источника зависят от напряжения или тока в каком-либо другом месте схемы.

 Управляемый напряжением источник напряжения показан на рис. 1.5.1.а. Уравнения этого четырехполюсника таковы:

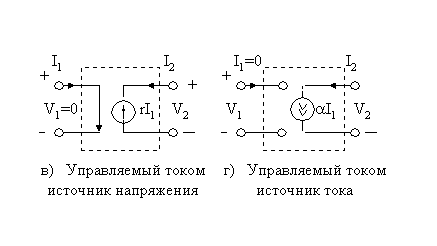
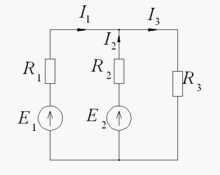
Билет 9 Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 1.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R₁ и R₂ (рис. 1.2) находятся в параллельных ветвях.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Схема на рис. 1.2 имеет три ветви: ветвь bma, в которую включены элементы r₀,E,R и в которой возникает ток I; ветвь ab с элементом R₁ и током I₁; ветвь anb с элементом R₂ и током I₂.

Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 1.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.

1.2

Для уменьшения значения входного (питающего) напряжения используют делитель напряжения на резисторах. В нём, выходное напряжениеUвых зависит от значения входного (питающего) напряжения Uвх и значения сопротивления резисторов. В этом случае выходное напряжение Uвых связано с входным Uвх (без учета возможного сопротивления нагрузки) следующим соотношением:

Uвых = Uвх х (R2 / R1 + R2)

Делитель напряжения – наиболее часто применяемое соединение резисторов. Например, переменный резистор, используемый в качестве регулятора громкости Ваших компьютерных колонок, является делителем напряжения с изменяемыми сопротивлениями плеч, где он выполняет роль ограничителя амплитуды входного сигнала.

Так как, сопротивление нагрузки влияет на выходное напряжение Uвых делителя, для обеспечения точности делителя напряжения, необходимо выполнять правило : Значение резистора R2 должно быть приблизительно на два порядка меньше (в 100 раз) сопротивления нагрузки подключаемой к выходу делителя. Если Вам не нужна высокая точность, то эту разницу можно снизить до 10 раз.

      Используя закон Ома, и пренебрегая малым током нагрузки, делитель напряжения можно описать соотношением: 

Делитель тока

Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2ток I составляет часть общего тока Iвх, определяемую сопротивлениями резисторов Rl и R2, т.е. можно записать, что Iвых = Iвх х (R1 / R2 + R1)

Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя, а после выполнения определённой функции вернуть эту часть обратно.  Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток

На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.        Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Кирхгофа) и формуле параллельного соединения резисторов: 

       (1)               (15)               (7)

   Двухполюсник – это электрическая цепь, имеющая два выхода. Двухполюсники, содержащие источники электрической энергии, называют активными, а без таких источников – пассивными.

а

Б

Эквивалентная схема двухполюсника: а – пассивного, б – активного

Последовательное соединение двухполюсников

    – общий ток по первому закону Кирхгофа.

Параллельное соединение двухполюсников

 ;

Билет 10

Пассивные элементы электрических цепей

Резистивным сопротивлением называется идеализированный элемент электрической цепи, обладающий свойством необратимого рассеивания энергии. Графическое изображение этого элемента и его вольт-амперная характеристика показана на рисунке (а - нелинейное сопротивление, б -линейное сопротивление).

Напряжение и ток на резистивном сопротивлении связаны между собой зависимостями: u = iR, i = Gu. Коэффициенты пропорциональности R и G в этих формулах называются соответственно сопротивлением и проводимостью и измеряются в омах [Ом] и сименсах [См]. R = 1/G.

Индуктивным элементом называется идеализированный элемент электрической цепи, обладающий свойством накопления им энергии магнитного поля. Графическое изображение этого элемента показано на рисунке (а - нелинейного, б - линейного).

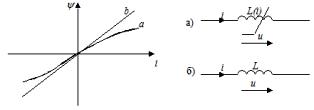
Линейная индуктивность характеризуется линейной зависимостью между потокосцеплением ψ и током i, называемой вебер-амперной характеристикой ψ= Li. Напряжение и ток связаны соотношением u = dψ/dt = L(di/dt)

Коэффициент пропорциональности L в формуле и называется индуктивностью и измеряется в генри (Гн).

Емкостным элементом (емкостью) называется идеализированный элемент электрической цепи, обладающий свойством накапливания энергии электрического поля. Графическое изображение этого элемента показано на рисунке. (а - нелинейного, б - линейного).

Линейная емкость характеризуется линейной зависимостью между зарядом и напряжением, называемой кулон-вольтовой характеристикой q = Cu

Напряжение и ток емкости связаны соотношениями i = dq/dt =C(du/dt)

Билет 11

АктАктивные элементы электрических цепей

Активными называются элементы цепи, которые отдают энергию в цепь, т.е. источники энергии. Существуют независимые и зависимые источники. Независимые источники: источник напряжения и источник тока.

Источник напряжения - идеализированный элемент электрической цепи, напряжение на зажимах которого не зависит от протекающего через него тока.

Внутреннее сопротивление идеального источника напряжения равно нулю.

Источник тока – это идеализированный элемент электрической цепи, ток которого не зависит от напряжения на его зажимах.

Внутреннее сопротивление идеального источника тока равно бесконечности.

Источники напряжения (тока) называются зависимыми (управляемыми), если величина напряжения (тока) источника зависит от напряжения или тока другого участка цепи. Зависимыми источниками моделируются электронные лампы, транзисторы, усилители, работающие в линейном режиме.

Различают четыре типа зависимых источников.

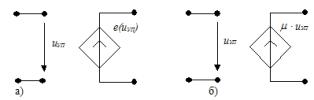
1. ИНУН – источник напряжения, управляемый напряжением: а) нелинейный, б) линейный, μ – коэффициент усиления напряжения

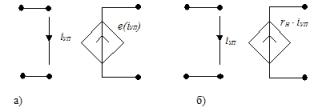
2. ИНУТ - источник напряжения, управляемый током: а) нелинейный, б) линейный, γн – передаточное сопротивление

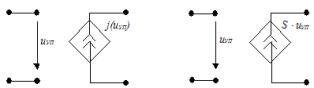
3. ИТУТ – источник тока, управляемый током: а) нелинейный, б) линейный, β - коэффициент усиления тока

4. ИТУН – источник тока, управляемый напряжением: а) нелинейный, б) линейный, S - крутизна (передаточная проводимость)

Условия эквивалентности источника напряжения и источника тока

Источник тока – это такой идеальный источник, который вырабатывает неизменную по величине силу электрического тока ( ) независимо от нагрузки.

Реальный источник тока – это такой источник, у которого внутреннее сопротивление не равно бесконечности ( ).

Докажем, что любому источнику с электродвижущей силой E и внутренним сопротивлением R_E (рис. 1.5, а) может быть найден источник тока J с тем же внутренним сопротивлением R_E (рис. 1.5, б).

Если U и I в цепях (рис. 1.5) равны, то обведенные контуром части схем эквивалентны.

Пусть сопротивления R_В в цепях (рис. 1.5) одинаковы. В цепи (рис. 1.5, а) ток можно определить по закону Ома:

.

(1.1)

В цепи (рис. 1.5, б) ток равен:  . С другой стороны:  , тогда

.

(1.2)

Сравнивая формулы (1.1) и (1.2), можно убедиться, что  . Это и есть условие эквивалентности источников.

Значит, доказано, что реальному источнику Е, R_в всегда можно найти реальный источник тока J, R_в. Но идеальному источнику Е нельзя найти эквивалентный идеальный источник J, так как внутренние сопротивления у них не могут быть одинаковыми (R_Е = 0, а R_J =  ) Билет 12

12. Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Последовательное соединение приемников поясняет рис. 25, а. .Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б. Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃. Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то длярассматриваемой цепи

U = U₁ + U₂ +U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов. Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁ : U₂ : U₃ = R₁ : R₂ : R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи. Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

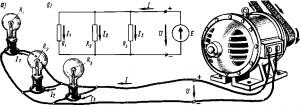Рис. 26. Схемы параллельного соединения приемников

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б. При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или

I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R_эк = 1/R₁ + 1/R₂ + 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается. Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-

Рис. 27. Схемы смешанного соединения приемников

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3. Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Определение эквивалентного сопротивления, напряжения и тока на отдельных резисторах – ДОДЕЛАТЬ111

13. Первый закон Кирхгофа (баланс токов) следует из непрерывности токов. Алгебраическая сумма токов в узле равна нулю. Закон выражает тот факт, что заряды в узле не накапливаются. Подтекающие токи берутся со знаком плюс, вытекающие со знаком минус. Второй закон Кирхгофа (баланс напряжений). Так как любая электрическая цепь является потенциальной, то алгебраическая сумма напряжений по замкнутому контуру равна алгебраической сумме э.д.с. этого контура. Напряжения и э.д.с., совпадающие с направлением обхода,  берутся со знаком плюс, иначе – со знаком минус.                                 . Общее число уравнений равно числу неизвестных токов. По первому закону составляется  уравнений, где  - число узлов. Остальные уравнения - по второму закону, причем ветви с источниками токов в контура не включаются, а в каждый новый контур должна войти хотя бы одна новая ветвь.

П ример1   пример 1

Пример 2.

Если требуется определить напряжение между двумя любыми точками цепи, то его можно включить в контур, например, для определения напряжения на источнике тока  в примере 1 составили уравнения для контура, помеченного пунктирной стрелкой: , откуда можно определить  . Закон Ома для сложной ветви.

По второму закону Кирхгофа для контура имеем:  , откуда  . Если  совпадает с направлением тока, то она берется со знаком плюс.

Закон сохранения энергии (баланс мощности) позволяет проверить правильность проведенных расчетов. Сумма мгновенных мощностей элементов цепи равна нулю: . Для примера 1:      . или   (баланс мощности).

Билет 14

14. Метод наложения — метод расчёта электрических цепей, основанный на предположении, что ток в каждой из ветвей электрической цепи при всех включённых генераторах, равен сумме токов в этой же ветви, полученных при включении каждого из генераторов по очереди и отключении остальных генераторов(только в линейных цепях).

Метод наложения используется как для расчёта цепей постоянного тока, так и для расчёта цепей переменного тока.

Найти ток   методом наложения в цепи, показанной на рисунке.  ,  ,    .

Пример метода наложения

При отключённом генераторе 2 ток   найдём по формуле:

.

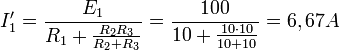При отключённом источнике 1, ток   будет

,

а ток   будет

.

Тогда ток   при обоих включённых источниках будет равен сумме токов   и  :

.

В задаче за положительные направления токов   и   приняты направления, совпадающие с направлением, показанным на рисунке для тока  . То же самое для тока 

Билет 15

15. Методика расчета цепи методом контурных токов

В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.

Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:

1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.

2 Определяем все независимые контуры.

3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.

4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5 Решаем любым методом полученную систему относительно контурных токов и определяем их.

6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

Пример расчёта сложной цепи методом контурных токов

В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом. 

Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов

Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).

По второму закону Кирхгофа относительно контурных токов составляем уравнения:

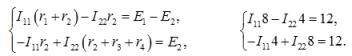
Решаем систему и получаем контурные токи I11 = I22 = 3 А.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.

Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.

Реальный ток второй ветви формируется двумя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 направлен навстречу реальному. В результате I2 = I22 - I11 = 3 - 3 = 0А.

В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для I3 можно записать I3 = -I22 = -3А.

Проверяем правильность нахождения токов в заданной электрической цепи методом узловых потенциалов. Согласно этому методу предполагается, что в каждом узле схемы имеется свой узловой ток который равен алгебраической сумме всех токов за счет проводимости ветвей. Этот метод основан на первом законе Кирхгофа и законе Ома.

Заземляем узел 3, φ3=0

Если в электрической схеме заземляется один из узлов, потенциал этой точки равен 0, а тока распределение не меняется.

Находим собственные проводимости ветвей присоединенных к оставшимся узлам 1,2,4. Собственная проводимость ветвей равна арифметической сумме проводимостей ветвей присоединенных к соответствующим узлам.

Находим взаимные проводимости, которые равны проводимости общих ветвей между соседними узлами.

Находим полный узловой ток, который равен сумме произведений ЭДС на соответствующую проводимость.

Составляем уравнение в соответствии с первым законом Кирхгофа.

Билет 17 http://demos.hut.ru/books/electrotexnical/sloshn.html

17. Под эквивалентными преобразованиями в электрической цепи подразумевается замена одних элементов другими таким образом, чтобы электромагнитные процессы в ней не изменились, а схема упрощалась. Одним из видов таких преобразований является замена нескольких потребителей, включённых последовательно или параллельно, одним эквивалентным.

Несколько последовательно соединённых потребителей можно заменить одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых последовательно. Для n потребителей можно записать:

rэ = r1 +r2+…+rn ,

где r1 , r2, ..., rn – сопротивления каждого из n потребителей.

При параллельном соединении n потребителей эквивалентная проводимость gэ равна сумме проводимостей отдельных элементов, включённых параллельно:

gэ= g1 + g2 +…+ gn .

Учитывая, что проводимость является обратной величиной по отношению к сопротивлению, можно эквивалентное сопротивление определить из выражения:

1/rэ = 1/r1 + 1/r2 +…+ 1/rn,

где r1, r2, ..., rn – сопротивления каждого из n потребителей, включённых параллельно.

В частном случае, когда параллельно включены два потребителя r1 и r2, эквивалентное сопротивление цепи:

rэ = (r1 х r2)/(r1 + r2)

Преобразования в сложных цепях, где отсутствует в явном виде последовательное и параллельное соединение элементов (рисунок 1), начинают с замены элементов, включённых в исходной схеме треугольником, на эквивалентные элементы, соединённые звездой. 

Рисунок 1. Преобразование элементов цепи: а - соединённых треугольником, б - в эквивалентную звезду

На рисунке 1, а треугольник элементов образуют потребители r1, r2, r3. На рисунке 1, б этот треугольник заменён эквивалентными элементами ra, rb, rc, соединёнными звездой. Чтобы не происходило изменение потенциалов в точках a, b, с схемы, сопротивления эквивалентных потребителей определяются из выражений:

Упрощение исходной цепи можно также осуществить заменой элементов, соединённых звездой, схемой, в которой потребители соединены треугольником.

В схеме, изображённой на рисунке 2, а, можно выделить звезду, образованную потребителями r1, r3, r4. Эти элементы включены между точками c, b, d. На рисунке 2, б между этими точками находятся эквивалентные потребители rbc, rcd, rbd, соединённые треугольником. Сопротивления эквивалентных потребителей определяются из выражений:

Рисунок 2. Преобразование элементов цепи: а - соединённых звездой, б - в эквивалентный треугольник

Дальнейшее упрощение схем, приведённых на рисунках 1, б и 2, б, можно осуществлять путём замены участков с последовательным и параллельным соединением элементов их эквивалентными потребителями.

При практической реализации метода расчёта простой цепи с помощью преобразований выявляются в цепи участки с параллельным и последовательным соединением потребителей, а затем рассчитываются эквивалентные сопротивления этих участков.

Если в исходной цепи в явном виде нет таких участков, то, применяя описанные ранее переходы от треугольника элементов к звезде или от звезды к треугольнику, проявляют их.

Данные операции позволяют упростить цепь. Применив их несколько раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Далее, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи.

Билет 18 Напряженность магнитного поля необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме.

Напряженность магнитного поля (формула) векторная физическая величина, равная:

Понравился материал? расскажи друзьям о сайте физика.

Напряженность магнитного поля в СИ - ампер на метр (А/м).

Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.

Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.

Величина, характеризующая способность вещества намагничиваться, называется магнитная проницаемость (µ). Она показывает, во сколько раз магнитная индукция в данном веществе больше или меньше магнитной индукции в вакууме.

Магнитная индукция в какой-либо точке поля в данной среде определяется по формуле

где   B – магнитная индукция в теслах;

I – величина тока в амперах;

L – расстояние от оси провода до исследуемой точки поля в метрах;

µ — магнитная проницаемость среды.

 

За единицу измерения магнитной проницаемости в Международной системе единиц принят 1 генри на метр.

Магнитная проницаемость среды равна 1 гн/м, если в точке, удаленной от оси проводника с током  на 1 метр, при силе тока, равной 2π ампера, магнитная индукция равна 1 тесле.

Величина магнитной проницаемости среды может быть выражена в виде произведения двух сомножителей

где   µ — магнитная проницаемость среды;

µ₀ – магнитная проницаемость вакуума;

µ_r – относительная магнитная проницаем ость, представляющая собой отвлеченное число, показывающее отношение величины магнитной проницаемости данного вещества к магнитной проницаемости вакуума.

Магнитная проницаемость вакуума µ₀ в Международной системе единиц равна

Магни́тная инду́кция   — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой   магнитное поле действует на заряд  , движущийся со скоростью  .

Более конкретно,   — это такой вектор, что сила Лоренца  , действующая со стороны магнитного поля^[1] на заряд  , движущийся со скоростью  , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора  перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

Магнитное поле характеризуется также величиной, носящей название магнитного потока. Магнитный поток можно представить (если условиться изображать его графически) общим числом маг­нитных линий, проходящих через всю рассматриваемую поверх­ность. В частности, под магнитным потоком Ф, проходящим через площадь S, перпендикулярную магнитным линиям, понимают про­изведение величины магнитной индукции В на величину площади, которая пронизывается этим магнитным потоком.

Ф = ВS.

Билет 19 19. Если к прямолинейному проводнику с электрическим током поднести магнитную стрелку, то она будет стремиться стать перпендикулярно плоскости, проходящей через ось проводника и центр вращения стрелки. Это указывает на то, что на стрелку действуют особые силы, которые называются магнитными силами. Кроме действия на магнитную стрелку, магнитное поле оказывает влияние на движущиеся заряженные частицы и на проводники с током, находящиеся в магнитном поле. В проводниках, движущихся в магнитном поле, или в неподвижных проводниках, находящихся в переменном магнитном поле, возникает индуктивная эдс.

Вокруг проводника с током образуется магнитное поле, так что свободно вращающаяся магнитная стрелка, помещенная вблизи проводника, будет стремиться занять положение, перпендикулярное плоскости, проходящей вдоль него. В этом легко убедиться, проделав следующий опыт. Магнитное поле  прямого проводника с током  В отверстие горизонтально положенного листа картона вставляют прямолинейный проводник и пропускают через него ток. Насыпают на картон железные опилки и убеждаются в том, что они располагаются концентрическими окружностями, имеющими общий центр в точке пересечения проводником картонного листа.  Магнитная стрелка, подвешенная на нити вблизи этого проводника, займет положение, указанное на рисунке. При изменении направления тока в проводнике магнитная стрелка повернется на угол 180°, оставаясь в положении, перпендикулярном плоскости, проходящей вдоль проводника.  В зависимости от направления тока в проводнике направление магнитных линий образуемого им магнитного поля определяется правилом буравчика, которое формулируется следующим образом:

Если поступательное движение буравчика совпадает с направлением тока в проводнике, то вращательное движение его рукоятки указывает направление магнитных линий поля, образующегося вокруг этого проводника.

Если по проволоке, согнутой в виде кольца, пропустить ток, то под действием его также возникнет магнитное поле. 

Билет 20

20. Магнитное поле катушки с током возникает в кольцевой катушке с W витками, равномерно распределенными вдоль немагнитного сердечника при подключении ее к источнику тока. Увеличение магнитной индукции поля достигается увеличением числа витков катушки и размещением ее на стальном сердечнике, магнитные токи которого, создавая свое поле, увеличивают результирующее поле катушки. Поверхность, ограниченная окружностью радиуса R, совпадающей со средней магнитной линией, пронизывается полным током ΣI = IW. Вследствие симметрии напряженность поля Н во всех точках, лежащих на средней магнитной линии, одинакова, поэтому мдс F_м = Hl = IW = H2πR. По закону полного тока Hl = IW, откуда напряженность магнитного поля на средней магнитной линии, совпадающей с осевой линией кольцевой катушки, H = IW / l , а магнитная индукция B = μ_aH = μ_aIW / l = 125μIW / l * 10^-8.

При R1 - R2 << Rl магнитную индукцию на осевой линии с достаточной точностью можно считать равной среднему значению ее, и, следовательно, магнитный поток сквозь поперечное сечение катушки Φ = BS = μ_aIWS / l . Переписав это уравнение в виде Φ = IW / (μ_aSl) = F_м / R_м , получим выражение, аналогичное уравнению закона Ома для электрической цепи, т. е. полный магнитный поток равен отношению мдс к магнитному сопротивлению цепи. Цилиндрическую катушку можно рассматривать как часть кольцевой катушки с большим радиусом и с обмоткой, расположенной только на части сердечника, длина которой равна длине катушки. Напряженность поля и магнитной индукции на осевой линии в центре цилиндрической катушки определяется по формулам, которые в этом случае являются приближенными и применимы для катушек.

В 1600 году английский ученый Уильям Гильберт в своей книге «О магните, магнитных телах  и большом магните - Земле». представил Землю, как гигантский постоянный магнит, ось которого  не совпадает с осью вращения Земли (угол между этими осями называют магнитным склонением).

Гильберт подтвердил свое предположение на опыте: он выточил из естественного магнита большой шар и, приближая к поверхности шара магнитную стрелку, показал, что она всегда устанавливается так же, как стрелка компаса на 3емле. Графически магнитное поле Земли похоже на магнитное поле постоянного магнита.

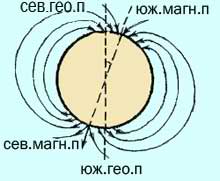
В 1702 году Э. Галлей создает первые магнитные карты Земли.  ___ Основная  причина  наличия  магнитного поля  Земли   в  том,  что  ядро  Земли   состоит  из  раскаленного  железа  (хорошего  проводника электрических  токов,  возникающих  внутри  Земли). ___ Магнитное поле Земли образует магнитосферу, простирающуюся на 70-80 тыс. км  в направление Солнца.  Она экранирует поверхность Земли, защищает от вредного влияния  заряженных частиц, высоких энергий и космических лучей, определяет характер погоды.

 Внутри кинескопа магнитное поле оказывает действие на поток электронов, движущихся в вакууме. Если электроны будут двигаться не в вакууме, а внутри проводника, создавая внутри его ток, то действие магнитного поля сохранится.Магнитное поле будет действовать на электроны, а те - на ионы проводника, внутри которого они движутся. В результате этого появится сила, приложенная ко всему проводнику с током.    Убедимся в этом на опыте. Соберем электрическую цепь, изображенную на рисунке 66, а. Замкнув цепь, мы увидим, как проводник AВ, подвешенный между полюсами магнита, придет в движение и установится в положении, изображенном на рисунке 66, б. Причиной смещения проводника является действие, оказываемое на него магнитным полем постоянного магнита.

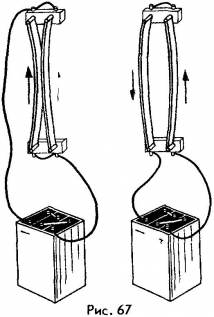
   Сила, с которой магнитное поле действует на проводник с током, называется силой Ампера.    Французский физик А. М. Ампер был первым, кто обнаружил действие магнитного поля на проводник с током. Правда, источником магнитного поля в его опытах был не магнит, а другой проводник с током. Помещая проводники с током рядом друг с другом, он обнаружил магнитное взаимодействие токов (рис. 67) - притяжение параллельных токов и отталкивание антипараллельных (т. е. текущих в противоположных направлениях). В опытах Ампера магнитное поле первого проводника действовало на второй проводник, а магнитное поле второго проводника - на первый. В случае параллельных токов силы Ампера оказывались направленными навстречу друг другу и проводники притягивались; в случае антипараллельных токов силы Ампера изменяли свое направление и проводники отталкивались друг от друга.

   Направление силы Ампера можно определить с помощью правила левой руки:    если расположить левую ладонь руки так, чтобы четыре вытянутых пальца указывали направление тока в проводнике, а силовые линии магнитного поля входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник с током (рис. 68).

   Эта сила (сила Ампера) всегда перпендикулярна проводнику, а также силовым линиям магнитного поля, в котором этот проводник находится.    Сила Ампера действует не при любой ориентации проводника. Если проводник с током расположить вдоль силовых линий магнитного поля, то это поле никакого действия на него не окажет.

Билет 21 21. Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.

Магнитным потоком Φ через площадь S контура называют величину 

Φ = B · S · cos α,

где B – модуль вектора магнитной индукции, α – угол между вектором   и нормалью   к плоскости контура (рис. 1.20.1).

Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали   и выбранное положительное направление   обхода контура связаны правилом правого буравчика

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называетсявебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м²: 

1 Вб = 1 Тл · 1 м2.

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции  _инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус: 

Эта формула носит название закона Фарадея.

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

Индуктированная э. д. с. возникает в следующих трех случаях:

когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого;

когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем э. д. с. (взаимоиндукция);

когда изменяющееся магнитное поле какого-либо проводника индуктирует в нем самом э. д. с. (самоиндукция).

Таким образом, всякое изменение во времени величины магнитного потока ( ), пронизывающего   проводящий контур   (виток, рамку),  сопровождается  появлением в этом  проводниковом контуре индуктированной э. д. с. е:

где ΔФ — магнитный поток, пересеченный проводником за промежуток времени Δt.

     Величина индуктированной э. д. с. в проводнике зависит:     от величины индукции В магнитного поля, так как чем плотнее Расположены магнитные линии, тем большее число их пересечет проводник за единицу времени (секунду);

скорости движения проводника V в магнитном поле, так как при большей скорости движения проводник может больше пересечь магнитных линий в секунду;   

от активной (находящейся в магнитном поле) длины проводника, так   как   длинный   проводник  может  больше  пересечь   магнитных   линий  в   секунду;

от величины синуса угла а между направлением движения проводника и направлением магнитного поля (рис. 93).

Раскладываем вектор скорости движения проводника в магнитном поле на две составляющие: Vн — составляющую, нормальную к направлению поля (Vн = V sin α), и V, — тангенциальную составляющую  (Vt = V cos α ), которая не принимает участия в создании з. д. с, так как при движении под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору В и не пересекал бы линий магнитной индукции.

Величина индуктированной э. д. с. может быть найдена по формуле

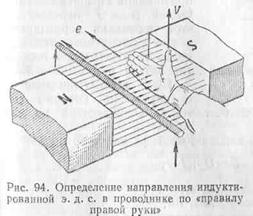
где В — величина магнитной индукции, тл; l — активная длина проводника, м;

V — скорость    движения  проводника, м/сек;

α— угол пересечения. Как было отмечено выше, направление индуктированной э. д. с.   зависит  от направления движения проводника и от направления магнитного поля.

Для определения направления индуктированной э. д. с. в проводнике, движущемся в магнитном поле, служит «правило правой руки». Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал  с направлением движения проводника, то четыре вытянутых пальца будут показывать направление э. д. с, индуктированной в проводнике (рис. 94).

В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной э. д. с. следует предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля,  и применить также «правило правой руки».

Билет 22

22. ЭДС индукции, наведённая в контуре – ДОДЕЛАТЬ111

В 1834 г. русский академик Э. X. Ленц, известный своими много­численными исследованиями в области электромагнитных явлений, дал универсальное правило для определения направления индукти­рованной э. д. с. в проводнике. Это правило, известное как пра­вило Ленца, может быть сформулировано так:

 направление индуктированной э. д. с. всегда таково, что вызван­ный ею ток и его магнитное поле имеют такое направление, что стремятся препятствовать причине, порождающей эту индуктиро­ванную э. д. с

 

С учетом этого правила можно закон электромагнитной индук­ции выразить более общей формулой, позволяющей определить не только величину, но и направление индуктированной э. д. с:

Выражение    представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток вре­мени ∆t, тем меньше вышеуказанная э. д. с. отличается от ее дей­ствительного значения в данный момент времени.

Знак минус, стоящий перед выражением  , определяет на­правление индуктированной э. д. с, т. е. учитывает правило Ленца.

При увеличении магнитного потока выражение   будет поло­жительным, а э. д. с. — отрицательной. В этом и заключается правило Ленца: э. д. с. и созданный ею ток противодействуют при­чине, которая их вызвала.

При  равномерном  изменении  во  времени магнитного  потока выражение  будет постоянно. Тогда абсолютное значение э. д. с. в проводнике будет равно

Если катушка состоит из w витков, соединенных между собой последовательно, то индуктированная э. д. с. в ней равняется сумме э. д. с, индуктированных в отдельных витках:

ЭДС индукции в катушке – ДОДЕЛАТЬ111

Потокосцепление — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности.

Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как   где   — магнитный поток одного витка

Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как   где   — магнитный поток одного витка

В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитный поток каждого витка одинаков. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:

где:  — количество витков;  — номер витка, с которым сцеплен поток 

В случае, если катушка имеет ферромагнитный сердечник, потокосцепление можно определить по формуле:

где   — магнитный поток через магнитопровод (сердечник) катушки.

Величина потокосцепления, помимо магнитного потока, имеет связь с током I в индуктивности, определяющуюся выражением:

где   — индуктивность катушки [ Гн ].

Эта формула выражает принцип непрерывности во времени потокосцепления катушки индуктивности.

Билет 23

Самоиндукция - явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

Замыкание цепи   При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи ( вихревое поле тормозит электроны). В результате Л1 загорается позже, чем Л2.

Размыкание цепи   При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток ( стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает. Вывод в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции?  Эл.ток создает собственное магнитное поле . Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике (B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника  (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.   Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:

где Ф - магнитный поток через контур, I - сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

 

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды  ( возможен сердечник).

ЭДС САМОИНДУКЦИИ

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? - выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

В формуле

 — магнитный поток,   — ток в контуре,   — индуктивность.

• Нередко говорят об индуктивности прямого длинного провода. В этом случае и других (особенно - в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током:

.

Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна  где I — сила тока в контуре.

Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна

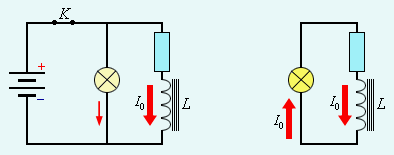
Энергия магнитного поля катушки.

Билет 24

24. ВЗАИМНАЯ ИНДУКТИВНОСТЬ, коэффициент взаимной индуктивности – величина, характеризующая отношение потокосцепления одной цепи (катушки) к току другой цепи (катушки), возбуждающему это потокосцепление. В Международной системе единиц (СИ) измеряется в генри (Г). Взаимная индуктивность зависит от числа витков катушек, их размеров и формы, взаимного расположения и магнитной проницаемости среды. Взаимная индуктивность двух катушек связана с их индуктивностью L₁ и L₂ следующим соотношением:

М = M _1-2 = М _2-1 = К / L ₁L ₂,

где К – коэффициент связи катушек, характеризующий степень их индуктивной связи; М – взаимная индуктивность, Г.

Коэффициент связи зависит от расположения катушек: при большем расстоянии между ними он уменьшается, при меньшем – увеличивается.Пусть две катушки, обладающие сопротивлениями R1 и R2 , индуктивностями L1 и L2 и взаимной индуктивностью M, соединены последовательно.

    Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой. Токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу. При встречном включении катушек конец второй присоединяется к концу первой.

Переменный ток долгое время не находил практического применения.  Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем

,

Величина, обратная периоду, есть частота,  измеряемая в герцах (Гц):

,

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота  f = 50Гц.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i  - мгновенное значение тока   ;

u – мгновенное значение напряжения   ;

е - мгновенное значение ЭДС   ;

р- мгновенное значение мощности   .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

  - амплитуда тока;

  - амплитуда напряжения;

  - амплитуда ЭДС.

Билет 25