
- •ЛОГИЧЕСКИЕ ОСНОВЫ
- •Основные определения математической логики
- •Логические функции могут быть описаны различными способами:
- •ПРЕДСТАВЛЕНИЕ ЛОГИЧЕСКОЙ ФУНКЦИИ В ВИДЕ ТАБЛИЦЫ ИСТИННОСТИ
- •ВСЕ ВОЗМОЖНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ ОТ ОДНОЙ ПЕРЕМЕННОЙ
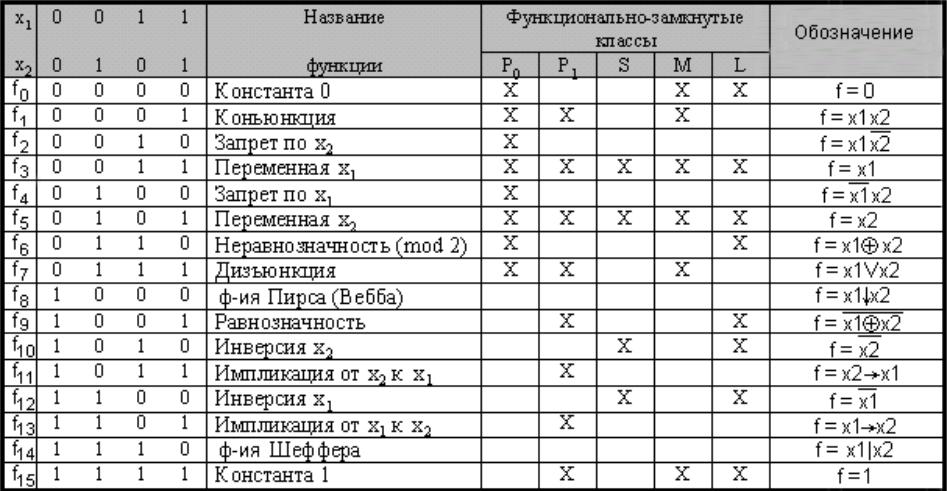
- •Все возможные логические функции от двух переменных
- •Все возможные логические функции от двух переменных
- •Все возможные логические функции от двух переменных
- •Штрих Шеффера (И-НЕ)
- •Стрелка Пирса (ИЛИ-НЕ)
- •Неравнозначность (сумма по mod2)
- •Представление логической функции в виде совершенных нормальных форм
- •Номер
- •Теорема 1. Любая функция алгебры логики (ФАЛ) может быть представлена аналитически в виде
- •Теорема 1. Любая функция алгебры логики (ФАЛ) может быть представлена аналитически в виде
- •Функция Фi, определяемая как
- •Номер
- •Теорема 2. Любая ФАЛ может быть представлена аналитически в виде f(x1 , x2,
- •Ранг терма r определяется количеством переменных, входящих в данный терм.
- •Элементарные конъюнкция и дизъюнкция — это те конъюнкции и дизъюнкции, в которых каждая
- •Повышение ранга ДНФ и КНФ
- •ЭКВИВАЛЕНТНОСТЬ ЛОГИЧЕСКИХ ФУНКЦИЙ
- •Полнота системы логических функций
- •Теорема. Пусть даны две системы логических функций:
- •Правила перехода от представления ФАЛ в виде ДНФ
- •Правила перехода от представления ФАЛ в виде КНФ
- •Свойства логических функций
- •При определении самодвойственности переключательной функции используется понятие противоположных наборов. Два набора аргументов называются
- •Переключательная функция называется самодвойственной, если на каждой паре противоположных наборов она принимает противоположные
- •При определении монотонности переключательной функции используется понятие сравнимости двух наборов аргументов.
- •Переключательная функция называется монотонной, если для всех пар сравнимых наборов при любом возрастании
- •Переключательная функция называется линейной, если она может быть представлена полиномом Жегалкина первой степени
- •Теорема Поста – Яблонского о функциональной полноте системы логических функций
- •Теорема Яблонского

Переключательная функция называется самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, т. е. если выполняется условие :
f (x1, x2, ..., xn ) = f* (x1, x2, ..., xn) = f (x1,x2,..., xn )
Пример самодвойственной функции: F(X1,X2,X3) = ∑(1,2,3,7)
Набор |
X1 |
X2 |
X3 |
F(X1,X2,X3) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
2 |
0 |
1 |
0 |
1 |
3 |
0 |
1 |
1 |
1 |
4 |
1 |
0 |
0 |
0 |
5 |
1 |
0 |
1 |
0 |
6 |
1 |
1 |
0 |
0 |
7 |
1 |
1 |
1 |
1 |
При определении монотонности переключательной функции используется понятие сравнимости двух наборов аргументов.
Примем условие, что 0 < 1. Два набора аргументов X = (x1, x2, ..., xn) и Z = ( z1, z2, ..., zn ) называются сравнимыми, если для всех аргументов выполняется условие xi ≤ zi (говорят, что X ≤ Z). Иными словами, если значение каждого аргумента одного набора меньше или равно значению того же аргумента второго набора, то говорят, что первый набор меньше или равен второму ( не больше второго ).
Например, если X = (0000) и Z = (0001), то наборы сравнимы и X < Z. Если же некоторые из значений аргументов первого набора больше
или равны, а другие меньше значений тех же аргументов второго набора, то такие наборы называются несравнимыми.
Например, если X = (1010) и Z = (0110), то наборы являются несравнимыми.

Переключательная функция называется монотонной, если для всех пар сравнимых наборов при любом возрастании набора значение этой функции не убывает, т.е. сохраняет свое значение или изменяется с 0 на 1. Иными словами,
если для сравнимых наборов X < Z , то f (X) |
f (Z). |
||
Т.е. для монотонной логической функции должно выполняться условие: |
|||
если для сравнимых наборов X < Z , то f (X) ≤ |
f (Z). |
||
Примеры: монотонная функция: F1(X1,X2) = X2 |
|||
немонотонная функция: F2(X1,X2) = X1 X 2 |
|||
X1 |
X2 |
F1(X1,X2) |
F2(X1,X2) |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Переключательная функция называется линейной, если она может быть представлена полиномом Жегалкина первой степени (каждая конъюнкция содержит только одну переменную), т.е. записана в виде :
f (x1, x2, ..., xn) = с0 с1x1 с2 x2 ... сnxn , где - символ операции "сумма по mod2»;
с0, с1, ..., сn – коэффициенты, равные 0 или 1.
Теорема Поста – Яблонского о функциональной полноте системы логических функций
Для того чтобы система переключательных функций была функционально полной, необходимо и достаточно, чтобы эта система включала:
-хотя бы одну переключательную функцию, не сохраняющую нуль;
-хотя бы одну переключательную функцию, не сохраняющую единицу;
-хотя бы одну нелинейную переключательную функцию;
-хотя бы одну немонотонную переключательную функцию;
-хотя бы одну несамодвойственную переключательную функцию.
Примеры функционально полных систем логических функций F1 = {&, V, ˉ } – «И-ИЛИ-НЕ»
F2 = {/} – «штрих Шеффера»
F3 = {↓} – «стрелка Пирса»
F4 = {«Сумма по mod2», «И», «Константа 1»} - «базис Жегалкина»
Теорема Яблонского
Из всякой полной системы логических функций можно выделить полную подсистему, содержащую не более 4-х ФАЛ.
Определение.
Система функций F={f1, f2,…,fn} называется базисом, если она полна, но всякая собственная подсистема не является полной.
