
- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
29 Синтетические бескупонные облигации: экономический смысл и нахождение.
Синтетическая бескупонная облигация – это инвестиционная стратегия, состоящая в приобретении и продаже купонных облигаций, генерирующая только один денежный поток в будущем. Размер этого будущего денежного потока соответствует номиналу бескупонной облигации. А размер денежного потока, генерируемого инвестиционной стратегией в настоящем, (взятый со знаком «плюс») соответствует текущей цене бескупонной облигации.
Пример. Пусть на финансовом рынке имеются двухлетние пятипроцентные и пятнадцатипроцентные облигации с номинальными стоимостями 100 д.е. (и с купонным периодом – один год). Цены этих облигаций, соответственно, равны 91,41 д.е. и 108,93 д.е. Требуется построить однолетние и двухлетние синтетические бескупонные облигации с номинальной стоимостью 100 д.е. , найти их цены и соответствующие чистые доходности.
Решение.
Пусть
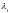 – количество приобретаемых (если
положительно) либо продаваемых (если
отрицательно) двухлетних пятипроцентных
облигаций, а
– количество приобретаемых (если
положительно) либо продаваемых (если
отрицательно) двухлетних пятипроцентных
облигаций, а
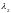 – количество приобретаемых (если
положительно) либо продаваемых (если
отрицательно) двухлетних
пятнадцатипроцентных облигаций.
– количество приобретаемых (если
положительно) либо продаваемых (если
отрицательно) двухлетних
пятнадцатипроцентных облигаций.
Очевидно,
что инвестиционная стратегия генерирует
в конце первого года денежный поток,
равный
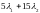 д.е.,
а в конце второго года –
д.е.,
а в конце второго года –
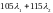 д.е.
Для однолетней синтетической бескупонной
облигации
и
находятся из системы уравнений:
д.е.
Для однолетней синтетической бескупонной
облигации
и
находятся из системы уравнений:
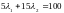 ,
,
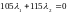 .
.
Решив
эту систему уравнений, получим:
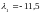 и
и
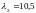 .
Таким образом, однолетняя синтетическая
бескупонная облигация состоит в продаже
11,5 двухлетних пятипроцентных облигаций
и в покупке 10,5 двухлетних пятнадцатипроцентных
облигаций. Цена однолетней синтетической
бескупонной облигации равна:
.
Таким образом, однолетняя синтетическая
бескупонная облигация состоит в продаже
11,5 двухлетних пятипроцентных облигаций
и в покупке 10,5 двухлетних пятнадцатипроцентных
облигаций. Цена однолетней синтетической
бескупонной облигации равна:
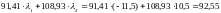 д.е.
д.е.
Теперь
мы можем найти чистую доходность для
одного года:
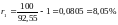 .
.
30 Использование чистых доходностей для дисконтирования денежных потоков облигации и экономический смысл найденной текущей стоимости облигации.
Рассмотрим на примере.
Допустим,
имеем чистые доходности для одного года
и для двух лет:
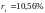 ,
,
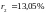 .
Используем эти чистые доходности для
дисконтирования платежей двухлетней
десятипроцентной облигации (с купонным
периодом – один год). Платежи двухлетней
десятипроцентной облигации с номинальной
стоимостью 100 д.е. (и с купонным периодом
– один год) равны 10 д.е. в конце первого
года и 110 д.е. в конце второго года. Для
дисконтирования платежей купонной
облигации используются чистые доходности,
соответствующие срокам платежей. Таким
образом,
.
Используем эти чистые доходности для
дисконтирования платежей двухлетней
десятипроцентной облигации (с купонным
периодом – один год). Платежи двухлетней
десятипроцентной облигации с номинальной
стоимостью 100 д.е. (и с купонным периодом
– один год) равны 10 д.е. в конце первого
года и 110 д.е. в конце второго года. Для
дисконтирования платежей купонной
облигации используются чистые доходности,
соответствующие срокам платежей. Таким
образом,
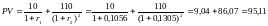 д.е.
д.е.
31.Форвардные доходности облигаций: нахождение и экономический смысл.
Под
форвардной доходностью
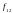 понимают такое значение доходности
,
при котором первая и вторая инвестиционная
стратегии обеспечивают одинаковый
доход в конце второго года, т.е. при
котором
понимают такое значение доходности
,
при котором первая и вторая инвестиционная
стратегии обеспечивают одинаковый
доход в конце второго года, т.е. при
котором
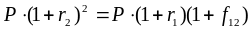 .
Итак, форвардная доходность
определяется из уравнения (4. Решив это
уравнение, получим:
.
Итак, форвардная доходность
определяется из уравнения (4. Решив это
уравнение, получим:
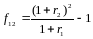 .
В случае, если на финансовом рынке
отсутствуют бескупонные облигации, то
при определении форвардной доходности
используются доходности синтетических
бескупонных облигаций (чистые доходности).
.
В случае, если на финансовом рынке
отсутствуют бескупонные облигации, то
при определении форвардной доходности
используются доходности синтетических
бескупонных облигаций (чистые доходности).
Данное
выше определение форвардной доходности
естественным образом обобщается на
случай
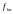 .
А именно, форвардная доходность
– это такое значение доходности
бескупонных облигаций со сроком погашения
в конце периода времени n,
найденная с помощью рыночной цены таких
облигаций в начале периода
.
А именно, форвардная доходность
– это такое значение доходности
бескупонных облигаций со сроком погашения
в конце периода времени n,
найденная с помощью рыночной цены таких
облигаций в начале периода
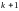 ,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
Вложить деньги в бескупонные облигации со сроком погашения в конце периода n.
Вложить деньги в бескупонные облигации со сроком погашения в конце периода k. Затем, в начале периода реинвестировать доход в бескупонные облигации со сроком погашения в конце периода n.
В соответствии с данным определением, форвардная доходность находится из уравнения:
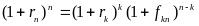 ,где
,где
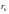 – доходность бескупонных облигаций со
сроком погашения в конце периода k,
а
– доходность бескупонных облигаций со
сроком погашения в конце периода k,
а
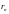 – доходность бескупонных облигаций со
сроком погашения в конце периода n.
– доходность бескупонных облигаций со
сроком погашения в конце периода n.
В
случае, если на финансовом рынке
отсутствуют бескупонные облигации, то
при определении форвардной доходности
используются доходности синтетических
бескупонных облигаций (чистые доходности).
Решив уравнение, получим:
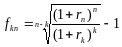 .
Иногда при определении форвардных
доходностей удобно использовать аппарат,
разработанный в случае непрерывной
капитализации процента. Дадим определение
(непрерывно капитализируемой) форвардной
доходности
.
Иногда при определении форвардных
доходностей удобно использовать аппарат,
разработанный в случае непрерывной
капитализации процента. Дадим определение
(непрерывно капитализируемой) форвардной
доходности
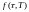 .
Форвардная доходность
– это такое значение (непрерывно
капитализируемой) доходности бескупонных
облигаций со сроком погашения в момент
времени T,
найденная с помощью рыночной цены таких
облигаций в момент времени
,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
.
Форвардная доходность
– это такое значение (непрерывно
капитализируемой) доходности бескупонных
облигаций со сроком погашения в момент
времени T,
найденная с помощью рыночной цены таких
облигаций в момент времени
,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
Вложить деньги в бескупонные облигации со сроком погашения в момент времени T.
Вложить деньги в бескупонные облигации со сроком погашения в момент времени и реинвестировать доход (полученный в момент времени ) в бескупонные облигации со сроком погашения в момент времени T.
В соответствии с данным определением, форвардная доходность находится из уравнения:
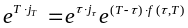 ,
где
,
где
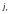 – непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времени
,
а
– непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времени
,
а
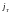 – непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времени T.
Очевидным образом уравнение (48) сводится
к следующему уравнению:
– непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времени T.
Очевидным образом уравнение (48) сводится
к следующему уравнению:
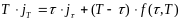 .Решив
это уравнение, получим:
.Решив
это уравнение, получим:
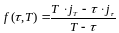 .
.
