26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)

Облигация – это обязательство организации, выпустившей облигацию, (эмитента) перед лицом, купившим облигацию, во-первых, погасить облигацию в конце оговоренного срока, и во-вторых, периодически выплачивать так называемые купонные платежи Размер купонного платежа R находится следующим образом. Обычно известна номинальная годовая купонная ставка j_куп и число купонных платежей в году m_куп . Вначале нужно определить эффективную купонную ставку для купонного периода r_куп по форму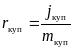ле: Затем с помощью номинала облигации F и эффективной купонной ставки для купонного периода r_куп находится размер купонного платежа R по формуле: 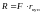.Где F – номинальная стоимость облигации. Текущая стоимость облигации показывает начальные инвестиции в альтернативные проекты с таким же финансовым риском как у данной облигации, обеспечивающие в будущем последовательность платежей, равных платежам облигации.

текущая стоимость облигации находится по формуле: 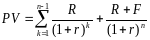,где r – внутренняя доходность альтернативных проектов. 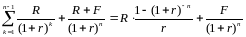(4) Подставив правую часть равенства (4) в правую часть формулы (3), получим:

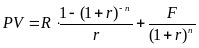
27. Доходность к погашению облигации: уравнение и экономический смысл.

Внутреннюю доходность облигации называют доходностью к погашению облигации. Эффективная доходность к погашению облигации для купонного периода – это процентная ставка r, при которой 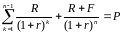, где P – рыночная цена облигации в текущий момент времени. С помощью формулы для суммы членов геометрической прогрессии левая часть уравнения сводится к следующему виду: 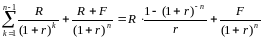. Таким образом, уравнение (1) принимает вид: . 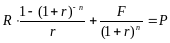Таким образом, эффективная доходность к погашению облигации для купонного периода – это такая эффективная банковская процентная ставка для купонного периода, при которой банковский начальный капитал, обеспечивающий последовательность платежей, равных платежам облигации, равен рыночной цене облигации в текущий момент времени.

28. Чистые доходности облигаций, их экономический смысл и методы нахождения.

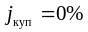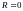Чистая доходность – это доходность к погашению бескупонной облигации,т.е. облигации, не выплачивающей купонные платежи ( ). Поскольку в случае бескупонной облигации , уравнение принимает вид: 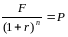. Решив это уравнение, получим следующую формулу для нахождения чистой доходности: 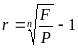. Чистая доходность, найденная по формуле (2) – это эффективная доходность для заданного промежутка времени.

Нахождение чистых доходностей методом наименьших квадратов На практике обычно количество видов облигаций m намного превышает количество n моментов времени, в которые выплачиваются платежи облигаций. В таких случаях чаще всего система уравнений 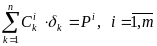(1) не имеет точного решения 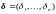. Однако можно найти приближенное решение этой системы.

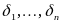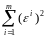Приближенной решение системы (1) состоит в подборе таких значений , чтобы сумма квадратов отклонений левых частей уравнений системы (1) от правых частей уравнений этой системы была минимальна, т.е. минимизируется , где .
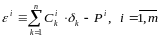