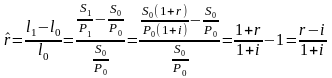- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
20 Анализ чувствительности денежных потоков проекта
А-з чувствит-и денеж потоков инвест проекта – это анализ того, как изменятся денеж потоки проекта при изменении одного или нескольких влияющих на них факторов. Введем следующие обозначения для основных параметров модели. Q – годовой выпуск продукции; p – ожидаемая цена; v – переменные издержки; F – постоянные издержки за один год; Io– начальные инвестиции; n – срок проекта в годах; t – налоговая ставка; r – ставка дисконтирования денеж потоков проекта.
В общем виде формула для нахождения годового денеж потока в условиях рассматриваемой модели – следующая
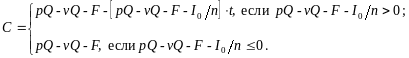 Найдем
частную производную от денежного потока
по объему производства.
Найдем
частную производную от денежного потока
по объему производства.
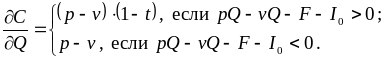 Частная
производная
Частная
производная
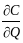 показывает на сколько денеж единиц
изменится денеж поток при увеличении
годового выпуска продукции на 1 ед-цу.
Данное утверждение справедливо в общем
случае (а не только для ожидаемых значений
параметров модели). Для любой
дифференцируемой функции
показывает на сколько денеж единиц
изменится денеж поток при увеличении
годового выпуска продукции на 1 ед-цу.
Данное утверждение справедливо в общем
случае (а не только для ожидаемых значений
параметров модели). Для любой
дифференцируемой функции
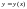 при достаточно малом изменении
при достаточно малом изменении
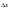 аргумента
x
имеет место
приближенное равенство
аргумента
x
имеет место
приближенное равенство
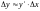 ,
где
,
где
 – производная функции y
по аргументу x.
Причем, если функция
– производная функции y
по аргументу x.
Причем, если функция
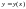 –
линейная. Т.к. денеж поток можно
рассматривать как (линейную) функцию
от объема производства то следует, что
–
линейная. Т.к. денеж поток можно
рассматривать как (линейную) функцию
от объема производства то следует, что
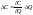 при достаточно малом
при достаточно малом
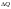 .
Аналогично можно найти частные производные
от денеж потока по другим параметрам.
Экономич смысл этих частных производных
такой же как у
.
Аналогично можно найти частные производные
от денеж потока по другим параметрам.
Экономич смысл этих частных производных
такой же как у
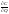 ,
т.е. частная производная от денеж потока
по соответствующему параметру показывает
на сколько денеж единиц изменится денеж
поток при увеличении параметра на
1ед-цу. Особого внимания заслуживает
частная производная по налоговой ставке.
Для изменения денеж потока при изменении
налоговой ставки формула примет вид
,
т.е. частная производная от денеж потока
по соответствующему параметру показывает
на сколько денеж единиц изменится денеж
поток при увеличении параметра на
1ед-цу. Особого внимания заслуживает
частная производная по налоговой ставке.
Для изменения денеж потока при изменении
налоговой ставки формула примет вид
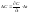 .
До сих пор мы
считали, что может меняться только
какой-либо один из параметров модели.
При одновременном изменении нескольких
параметров изменение денежного потока
определяется по формуле
.
До сих пор мы
считали, что может меняться только
какой-либо один из параметров модели.
При одновременном изменении нескольких
параметров изменение денежного потока
определяется по формуле
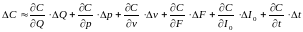 .
.
Анализ безубыточности инвестиционного проекта.
Безубыточный
проект – проект, чистая текущая стоимость
которого неотрицательна, (т.е. внутренняя
доходность которого не меньше внутренней
доходности альтернативных проектов с
таким же финансовым риском как у данного
проекта). Чистая текущая стоимость
проекта определяется по формуле:
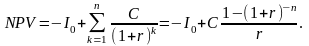 Из
этой формулы следует, что чистая текущая
величина данного проекта неотрицательна
тогда и только тогда, когда
Из
этой формулы следует, что чистая текущая
величина данного проекта неотрицательна
тогда и только тогда, когда
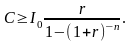 Величину
Величину
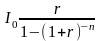 обозначим буквой R
Итак,
рассматриваемый проект безубыточен
тогда и только тогда, когда его годовой
свободный денежный поток больше либо
равен R,
т.е.
обозначим буквой R
Итак,
рассматриваемый проект безубыточен
тогда и только тогда, когда его годовой
свободный денежный поток больше либо
равен R,
т.е.
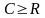 .
.
Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
Уровень
инфляции i
за период времени определяется по
формуле:
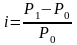 .
где
.
где
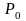 и
и
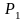 – цены потребительской корзины в начале
и в конце периода времени равны,
соответственно. Пусть r
– номинальная банковская процентная
ставка за период времени. Тогда сумма
– цены потребительской корзины в начале
и в конце периода времени равны,
соответственно. Пусть r
– номинальная банковская процентная
ставка за период времени. Тогда сумма
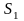 ,
наращенная за период времени при
начальном капитале
,
наращенная за период времени при
начальном капитале
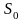 ,
равна:
,
равна:
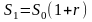 .
В начале периода за начальный капитал
можно
купить
.
В начале периода за начальный капитал
можно
купить
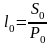 потребительских корзин. В конце периода
за наращенную сумму
можно
купить
потребительских корзин. В конце периода
за наращенную сумму
можно
купить
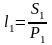 потребительских корзин. Реальная
процентная ставка
потребительских корзин. Реальная
процентная ставка
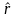 определяется по формуле:
определяется по формуле:
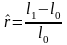 и показывает на сколько процентов больше
потребительских корзин можно купить в
конце периода за наращенную сумму, чем
в начале периода за начальный капитал.
Взаимосвязь между реальной процентной
ставкой, номинальной процентной ставкой
и уровнем инфляции выражается след
формулой:
и показывает на сколько процентов больше
потребительских корзин можно купить в
конце периода за наращенную сумму, чем
в начале периода за начальный капитал.
Взаимосвязь между реальной процентной
ставкой, номинальной процентной ставкой
и уровнем инфляции выражается след
формулой: