
- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
Чистая
текущая стоимость инвестиционного
проекта показывает, на сколько денег в
начальный момент времени нужно вложить
меньше в инвестиционный проект , чем в
банк для того, чтобы обеспечить
последовательность платежей, равных
свободным денежным потокам инвестиционного
проекта.
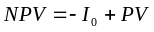 ,
где I0
– начальн инв-ции и PV
–текущ стоим-ть
,
где I0
– начальн инв-ции и PV
–текущ стоим-ть
Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
Внутр
доходность инвест проекта (IRR)
– это такая банковская % ставка, при
которой банковский начальный капитал,
обеспечивающий последовательность
платежей, равных (ожидаемым) свободным
денежным потокам инвестиционного
проекта, равен начальным инвестициям
в проект. Т.е. это % ставка r,
при которой
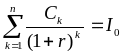 .
.
17 Модель с постоянным процентным ростом свободных денежных потоков
При
оценке свободных денежных потоков
инвест проекта с достаточно большим
(неограниченным) сроком удобно считать,
что начиная с некоторого периода времени
%-й рост свободных денежных потоков
становится const.
Предположим, что при некотором n
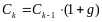 для всех
для всех
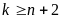 ,
где коэффициент g
не зависит от k.
g
показывает относительное изменение
свободных денежных потоков (сдп). Будем
называть его коэффициентом роста сдп.
Следует, что
,
где коэффициент g
не зависит от k.
g
показывает относительное изменение
свободных денежных потоков (сдп). Будем
называть его коэффициентом роста сдп.
Следует, что
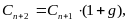
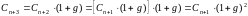 ,
и т.д. По индукции получаем:
,
и т.д. По индукции получаем:
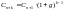 .
Рыноч стоимость проекта в начале (n+1)-го
периода равна сумме дисконтированных
сдп начиная с (n+1)-го
периода:
.
Рыноч стоимость проекта в начале (n+1)-го
периода равна сумме дисконтированных
сдп начиная с (n+1)-го
периода:
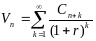 .
Получим:
.
Получим: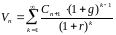 .
Когда
.
Когда
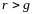 ,
последнее выражение несложно привести
к следующему виду:
,
последнее выражение несложно привести
к следующему виду: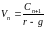 . В
случае, когда
. В
случае, когда
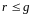 ,
,
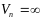 (что не реально). В дальнейшем будем
считать, что
(что не реально). В дальнейшем будем
считать, что
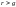 .
.
18 Задача оптимального финансирования проекта
Предположим,
что проект требует инвестиций
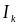 ,
,
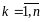 ,
в конце n
периодов времени. Для финансир-я проекта
фирма в начальный момент времени создает
инвест фонд, размером
д.е. Инвест фонд должен обеспечить
выплату требуемых денежных сумм
,
,
в конце n
периодов времени. Для финансир-я проекта
фирма в начальный момент времени создает
инвест фонд, размером
д.е. Инвест фонд должен обеспечить
выплату требуемых денежных сумм
,
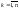 ,
в моменты времени 1, 2, …, n.
При этом фирма имеет возмож-ть вкладывать
деньги из инвест фонда в m
видов фин инструментов. Момент времени,
когда деньги вкладываются в фин
инструменты вида i,
обозначим
,
в моменты времени 1, 2, …, n.
При этом фирма имеет возмож-ть вкладывать
деньги из инвест фонда в m
видов фин инструментов. Момент времени,
когда деньги вкладываются в фин
инструменты вида i,
обозначим
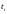 ,
а когда фин инстр-ты вида i
обеспеч доход, – через
,
а когда фин инстр-ты вида i
обеспеч доход, – через
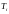 .
(
.
(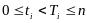 .)
Эфф доходность финн инструментов вида
i
обозначим через
.)
Эфф доходность финн инструментов вида
i
обозначим через
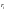 .
Уровень финансового риска, связанного
с вложением денег в инструменты вида
i,
обозначим через
.
Уровень финансового риска, связанного
с вложением денег в инструменты вида
i,
обозначим через
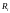 .
Задача фирмы- min
начальные вложения
.
Задача фирмы- min
начальные вложения
 в инвест фонд. При этом в течение каждого
периода времени средневзвешенный
уровень риска, связанный с вложением
денег из инвест фонда в фин инструменты,
не должен превышать
в инвест фонд. При этом в течение каждого
периода времени средневзвешенный
уровень риска, связанный с вложением
денег из инвест фонда в фин инструменты,
не должен превышать
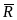 .Построим
матем модель. Количество денег,
вкладываемых фирмой в финансовые
инструменты вида i,
обозначим через
.Построим
матем модель. Количество денег,
вкладываемых фирмой в финансовые
инструменты вида i,
обозначим через
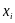 .
В начал момент времени вложения
в инвест фонд вкладываются в финансовые
инструменты для которых
.
В начал момент времени вложения
в инвест фонд вкладываются в финансовые
инструменты для которых
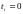 .
Следовательно,
.
Следовательно,
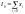 .
Математ постановка задачи оптимального
финанс-я проекта: минимизировать целевую
функцию
.
Математ постановка задачи оптимального
финанс-я проекта: минимизировать целевую
функцию
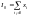 при ограничениях и условии неотрицательности
переменных
при ограничениях и условии неотрицательности
переменных
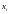 ,
,
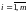 ,
т.е.
,
т.е.
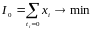 ,
,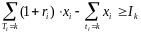 ,
,
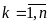 ,
, 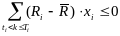 ,
,
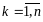 ,
,
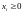 ,
.
(написать эти формулы в столбик)
,
.
(написать эти формулы в столбик)
19 Задача оптимального выбора инвестиционных проектов
Предположим
фирма может принять m
инвест проектов. Чистая тек стоимость
каждого проекта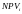 ,
,
которые требует инвестиций в течение
n
периодов времени.
,
,
которые требует инвестиций в течение
n
периодов времени.
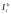
размер инвестиций, требуемых для i-го
проекта в k-том
периоде. Для финанс-я всех отобранных
проектов фирма располагает в k-том
периоде суммой
размер инвестиций, требуемых для i-го
проекта в k-том
периоде. Для финанс-я всех отобранных
проектов фирма располагает в k-том
периоде суммой
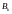 д.е. Задача
отобрать проекты таким образом, чтобы
их суммарная чистая тек стоимость была
макс и при этом, чтобы в каждом периоде
суммарные инвестиции не превышали
выделенных сумм
.
Чтобы построить матем модель введем
двоичные переменные
,
.
Положим
д.е. Задача
отобрать проекты таким образом, чтобы
их суммарная чистая тек стоимость была
макс и при этом, чтобы в каждом периоде
суммарные инвестиции не превышали
выделенных сумм
.
Чтобы построить матем модель введем
двоичные переменные
,
.
Положим
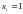 в случае, если i-й
проект принимается, и
в случае, если i-й
проект принимается, и
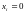 в случае, если i-й
проект отвергается. Тогда суммарная
тек стоимость отобранных проектов будет
равна
в случае, если i-й
проект отвергается. Тогда суммарная
тек стоимость отобранных проектов будет
равна
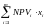 ,
а суммарные инвестиции, требуемые в
k-том
периоде для финанс-я отобранных проектов
–
,
а суммарные инвестиции, требуемые в
k-том
периоде для финанс-я отобранных проектов
–
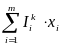 .
Математ модель задачи:
.
Математ модель задачи:
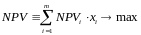 ,
, 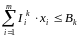 ,
,
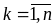 ,
,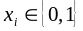 ,
,
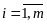 .
(написать эти формулы в столбик)
.
(написать эти формулы в столбик)
