
- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
Вечная рента: вывод формул для текущей стоимости и продолжительности.
Если
число рентных платежей не ограничено
(т.е.
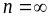 ),
рента называется вечной.
),
рента называется вечной.
Текущая
стоимость ренты В
случае вечной ренты с помощью формулы
для суммы бесконечной геометрической
прогрессии имеем:
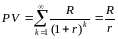 .
Таким образом, в случае вечной ренты
.
Таким образом, в случае вечной ренты
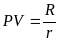 ,
где r
– эффективная процентная ставка для
рентного периода. Будущая
стоимость ренты
,
где r
– эффективная процентная ставка для
рентного периода. Будущая
стоимость ренты
Воспользовавшись
формулой для суммы геометрической
прогрессии, получим:
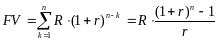 .
Итак,
.
Итак,
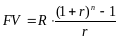 ,
где r
– эффективная процентная ставка для
рентного периода. Продолжительность
ренты Для
нахождения продолжительности ренты
воспользуемся формулой (15). Вначале
найдем продолжительность вечной ренты.
Текущая стоимость вечной ренты
определяется по формуле (25). Возьмем
производную от PV
по r:
,
где r
– эффективная процентная ставка для
рентного периода. Продолжительность
ренты Для
нахождения продолжительности ренты
воспользуемся формулой (15). Вначале
найдем продолжительность вечной ренты.
Текущая стоимость вечной ренты
определяется по формуле (25). Возьмем
производную от PV
по r:
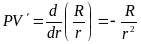 .
Подставим эту формулу и формулу (25) в
(15). В результате получим:
.
Подставим эту формулу и формулу (25) в
(15). В результате получим:
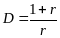 . Отметим, что процентная ставка r,
фигурирующая в формуле (28) – это
эффективная процентная ставка для
рентного периода.
. Отметим, что процентная ставка r,
фигурирующая в формуле (28) – это
эффективная процентная ставка для
рентного периода.
Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
Под инвестиционным проектом будем понимать любое вложение денег с целью получения прибыли в будущем. Свободный денежный поток представляет собой разность прибыли и инвестиций в заданном периоде времени, т.е.
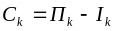 , где
–
свободный денежный поток в k-том
периоде,
, где
–
свободный денежный поток в k-том
периоде,
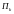 – прибыль в k-том
периоде,
– прибыль в k-том
периоде,
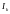 – инвестиции в k-том
периоде. Отметим, что в большинстве
случаев в начальный момент времени
точные значения прибыли и инвестиций
в будущем не известны. Поэтому, под
,
и
подразумеваются ожидаемые значения
соответствующих параметров. Часто
свободные денежные потоки инвестиционного
проекта можно оценить с достаточной
точностью лишь на некоторое ограниченное
количество лет вперед. (Такое количество
лет называют горизонтом
оценивания свободных денежных потоков
инвестиционного проекта.) При этом, тем
не менее, можно достаточно точно оценить
рыночную стоимость проекта в конце
горизонта оценивания. В таких случаях
при нахождении текущей (и чистой текущей)
стоимости проекта дисконтируется
рыночная стоимость проекта в конце
горизонта оценивания, т.е.
– инвестиции в k-том
периоде. Отметим, что в большинстве
случаев в начальный момент времени
точные значения прибыли и инвестиций
в будущем не известны. Поэтому, под
,
и
подразумеваются ожидаемые значения
соответствующих параметров. Часто
свободные денежные потоки инвестиционного
проекта можно оценить с достаточной
точностью лишь на некоторое ограниченное
количество лет вперед. (Такое количество
лет называют горизонтом
оценивания свободных денежных потоков
инвестиционного проекта.) При этом, тем
не менее, можно достаточно точно оценить
рыночную стоимость проекта в конце
горизонта оценивания. В таких случаях
при нахождении текущей (и чистой текущей)
стоимости проекта дисконтируется
рыночная стоимость проекта в конце
горизонта оценивания, т.е.
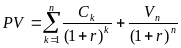 .
(Здесь n
– горизонт оценивания,
.
(Здесь n
– горизонт оценивания,
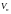 – рыночная стоимость проекта в конце
горизонта оценивания.
– рыночная стоимость проекта в конце
горизонта оценивания.
Текущая стоимость инвестиционного проекта: формула и экономический смысл.
Пусть
инвестиционный проект генерирует
свободные денежные потоки
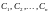 в течение n
периодов времени. Начальные инвестиции
в проект равны
в течение n
периодов времени. Начальные инвестиции
в проект равны
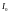 .
Вместо того, чтобы инвестировать деньги
в инвестиционный проект, можно положить
деньги в банк под процент. Начальный
капитал (положенный в банк под процент),
обеспечивающий последовательность
платежей, равных (ожидаемым) свободным
денежным потокам инвестиционного
проекта, можно найти по формуле:
.
Вместо того, чтобы инвестировать деньги
в инвестиционный проект, можно положить
деньги в банк под процент. Начальный
капитал (положенный в банк под процент),
обеспечивающий последовательность
платежей, равных (ожидаемым) свободным
денежным потокам инвестиционного
проекта, можно найти по формуле:
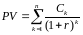 ,
где r
– эффективная банковская процентная
ставка для одного периода времени.
Процентную ставку, используемую при
дисконтировании свободных денежных
потоков инвестиционного проекта,
называют ставкой дисконтирования
свободных денежных потоков инвестиционного
проекта.
,
где r
– эффективная банковская процентная
ставка для одного периода времени.
Процентную ставку, используемую при
дисконтировании свободных денежных
потоков инвестиционного проекта,
называют ставкой дисконтирования
свободных денежных потоков инвестиционного
проекта.
