9. Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.

Стоимость последовательности платежей в произвольный момент времени будем понимать количество денег, которое обеспечивается заданной последовательностью платежей в момент времени 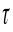. 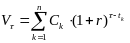,(10) где r – эффективная процентная ставка для периодов времени, в которых выражены сроки платежей .

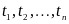10. Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.

Продолжительность последовательности платежей – средневзвешенный срок выплаты платежей, в котором в качестве весов фигурируют доли текущих стоимостей отдельно взятых платежей в текущей стоимости последовательности платежей. Продолжительность последовательности платежей обозначают буквой 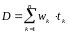,(12) где 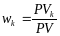, 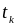– срок выплаты k-го платежа. (Здесь 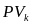– текущая стоимость k-го платежа, 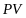– текущая стоимость последовательности платежей, т.е. 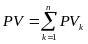. Продолжительность последовательности платежей играет важную роль при оценке чувствительности текущей стоимости последовательности платежей по отношению к изменению процентной ставки.

Оценка чувствительности текущей стоимости последовательности платежей по отношению к изменению процентной ставки. Для оценки чувствительности текущей стоимости одного платежа: 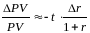(31), где t – срок платежа. В случае последовательности платежей роль срока платежа в формуле (31) играет продолжительность последовательности платежей, т.е. имеет место следующая формула: 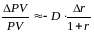.(13) Из формулы (13) => чем больше продолжительность последовательности платежей, тем сильнее чувствительность текущей стоимости последовательности платежей к изменению процентной ставки.

11. Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.

Финансовая (конечная) рента – это последовательность платежей, выплачиваемых через равные промежутки времени. Пусть t – срок ренты (в годах), 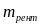– количество рентных платежей в году. Тогда количество всех рентных платежей (которое мы обозначим буквой n) можно найти по формуле:

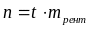.Текущая стоимость ренты Поскольку финансовая рента – частный случай последовательности платежей, текущая стоимость ренты может быть найдена с помощью формулы:

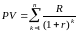,где r – эффективная процентная ставка для рентного периода. С помощью формулы для суммы геометрической прогрессии, выражение (23) несложно привести к следующему виду:

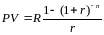. Будущая стоимость ренты Найдём будущую стоимость ренты 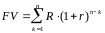Воспользовавшись формулой для суммы геометрической прогрессии, получим: 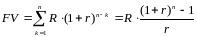. Итак, 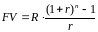, где r – эффективная процентная ставка для рентного периода. Продолжительность ренты Получим формулу для нахождения продолжительности ренты с конечным числом платежей. Текущая стоимость конечной ренты определяется по формуле (24). Возьмем производную от текущей стоимости конечной ренты по r: 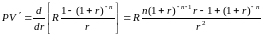. 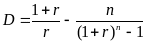Подставив это выражение и формулу (24) в (15) после несложных алгебраических преобразований получим: .Отметим, что процентная ставка r, фигурирующая в формуле (29) – это эффективная процентная ставка для рентного периода.