
- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
Задача
минимизации риска при ограничении на
ожидаемую доходность имеет вид:
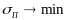 ,
,
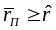 ,
,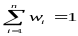 ,
, 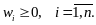
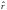 – заданное
минимально допустимое значение ожидаемой
доходности.
– заданное
минимально допустимое значение ожидаемой
доходности.
Геометрически решение задачи минимизации риска выглядит следующим образом.

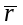
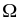
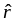
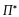
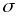
44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
Задача максимизации полезности инвестора имеет вид:
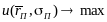 ,
,
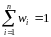 ,
,
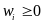 ,
,
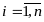 .
.
Переменные
в данной задаче – это доли
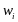 ,
,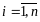 .
.
Функция
полезности
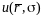 может
иметь, например, следующий вид:
может
иметь, например, следующий вид:
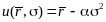 ,
,
где
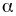 – положительная константа, описывающая
несклонность инвестора к риску.
– положительная константа, описывающая
несклонность инвестора к риску.
45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
Комбинация
безрискового актива
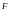 и фин актива
и фин актива
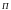 - частный случай инвест портфеля, где
- частный случай инвест портфеля, где
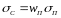 ,
,
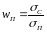 . (
. (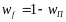 ),
),
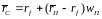 ,
(
,
(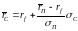 ).
Последняя формула – это уравнение
прямой в координатной плоскости
).
Последняя формула – это уравнение
прямой в координатной плоскости
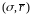 ,
проходящей через точки
,
проходящей через точки
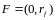 и
и
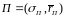 .
.
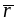
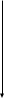

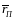
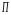
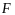
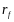
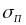
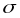
множество
инвест возможностей комбинаций
безрискового актива
и финансового актива
находится на прямой
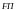 -
рыночной линией капитала, которая
зависит от актива
).
Множество инвест возможностей комбинаций
безрискового актива и всевозможных
портфелей фин активов – это множество
всех лучей
-
рыночной линией капитала, которая
зависит от актива
).
Множество инвест возможностей комбинаций
безрискового актива и всевозможных
портфелей фин активов – это множество
всех лучей
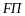 ,
где
,
где
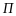 принадлежит множеству
принадлежит множеству
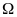 инвест возможностей портфелей финансовых
активов.
инвест возможностей портфелей финансовых
активов.


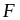
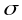
множество инвест возможностей комбинаций безрискового актива и всевозможных портфелей финансовых активов представляет собой угол, заключенный между самым верхним и самым нижним лучами, выходящими из точки проходящими (касающимися) через множество .


Эффективная граница множества инвестиционных возможностей комбинаций безрискового актива и портфелей фин активов – это самый верхний луч, выходящий из точки и проходящий через множество .
46 Оптимизация портфеля при наличии безрискового актива
М.7. Существует безрисковая ставка RQ, ПО которой инвесторы могут кредитовать и заимствовать произвольную сумму денег.
Будем полагать, что инвесторы формируют свои портфели сроком на один период владения на множестве активов, включающем N рисковых ценных бумаг и один безрисковый актив, одновременно решая задачу оптимального распределения капитала между рисковыми ценными бумагами. Прогнозные значения вектора ожидаемых доходностей активов и ковариационной матрицы доходностей активов для рассматриваемого периода равны: //=(///) и Е==Ет={а/,} (сг/рсг^О), причем матрица ? является положительно определенной.
Структура комбинированного портфеля инвестора задается величинами XQ, *Ь Х2, х^, которые удовлетворяют условию:
XQ + Х[ + Х2 +.. + Х]Ч = XQ + ^/=1,
где ЛГ=(х1, Х2, хуу)т - вектор, определяющий структуру рисковой части портфеля, a XQ—X-X^I И l-xo^A^/ - соответственно доли безрисковых и рисковых вложений инвестора.
Поскольку доходность безрискового актива — величина фиксированная (неслучайная), то ее дисперсия, а также кова-риация с доходностями других активов равна нулю.
Поэтому дисперсия доходности комбинированного портфеля активов обусловлена только присутствием в портфеле рисковых активов и определяется, как и ранее, по формуле
ар2 = Х*ЪХ. (5.36)
Если заданы значения безрисковой ставки RQ И ожидаемой (приемлемой для инвестора) доходности портфеля /ир, то структура оптимального в смысле подхода "доходность -риск" портфеля будет являться решением следующей задачи, известной как задача Тобина:
а) = ХТ?Х min, (5.37)
X^ju + (X-X^l)R0=MP. (5.38)
Данная задача, как и задача Марковица, допускает аналитическое решение с помощью метода неопределенных множителей Лагранжа. Функционал Лагранжа при этом имеет вид:
Л(Х9Я) = Х^ЪХ + Я(Мр - Хтм -(1 - ХТ1) RQ), (5.39) где Я - неопределенный множитель Лагранжа.
Дифференцируя Л по X и приравнивая к нулю вектор производных, получаем:
2ЪХ-Я{/л -RQI) = 0, откуда с учетом (5.38) следует:
лг=0ц^)Е.1О/_ЛЬЛ) (540) gp
где g2P = (M-Rol)Tz-l(M-Rol)- (5-41)
229 Оптимальному портфелю со структурой (5.40) соответствует минимальный риск, который с учетом (5.36) равен:
ар =(Х*12Г)1/2=(Мр-Яо)/8р,
откуда следует, что характеристика gp допускает представление:
gp = (Mp - Ro)/*p>0, (5.42)
т.е. равна величине ожидаемой дополнительной доходности (премии за риск), приходящейся на единицу риска, и может интерпретироваться как цена единицы риска на рассматриваемом множестве (рынке) рисковых ценных бумаг. Представим (5.42) в виде:
Hp-Ro = gpОтсюда следует, что, чем выше цена риска gp, тем больше ожидаемая премия за риск, т.е. тем выгоднее вложения в данный портфель.
Характеристика gj = (//0 известна как отношение Шарпа (Sharpe ratio), или индекс Шарпа, и используется для оценки привлекательности произвольного рискового актива или портфеля D с характеристиками JU^CT^ Очевидно, данная характеристика принимает максимальное значение для эффективных портфелей
47. Максимизация полезности инвестора при наличии безрискового актива. Задача максимизации полезности инвестора имеет вид:
![]() ,
,
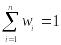 ,
,
![]() ,
,
![]() .
.
Переменные
в данной задаче – это доли
![]() ,
.
,
.
Функция
полезности
![]() может
иметь, например, следующий вид:
может
иметь, например, следующий вид:
![]() ,
,
где
![]() – положительная константа, описывающая
несклонность инвестора к риску.
– положительная константа, описывающая
несклонность инвестора к риску.
