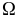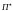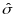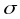- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
На основании данных о выполнении заемщиками взятых на себя обязательств по выплате займов наблюдения делят на несколько групп.
Обозначим
через
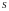 число групп наблюдений, через
число групп наблюдений, через
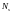 и
и
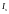 – соответственно, количество наблюдений
и множество индексов в группе
– соответственно, количество наблюдений
и множество индексов в группе
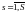
Для
каждой группы
находятся средние значения показателей
,
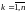 :
:
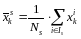 (30)
(30)
Вектор
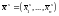 называется центроидом группы
называется центроидом группы
 .
.
Потенциального
заемщика с финансовыми показателями
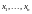 относят к той группе, к центороиду
которой «ближе» всего вектор
относят к той группе, к центороиду
которой «ближе» всего вектор
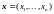 финансовых
показателей потенциального заемщика.
финансовых
показателей потенциального заемщика.
Для определения «близости» вектора к центроиду может, например, использоваться следующая мера:
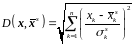 . (31)
. (31)
Здесь
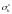 – выборочное стандартное отклонение
параметра
в группе
,
т.е.
– выборочное стандартное отклонение
параметра
в группе
,
т.е.
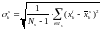 . (32)
. (32)
Итак,
потенциального заемщика относят к той
группе, для которой
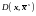 минимально.
минимально.
41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
Множество
инвест возможностей
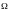 – это множество векторов
– это множество векторов
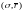 ,
таких, что существует инвест портфель,
стандартное отклонение доходности
которого =
,
таких, что существует инвест портфель,
стандартное отклонение доходности
которого =
 ,
и ожидаемая доходность которого =
,
и ожидаемая доходность которого =
 .
.
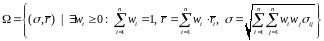 .
.
Эффективный
портфель - приносящий самую высокую
ожидаемую доходность при данном уровне
риска, или, соответственно, самый низкий
риск при данной ожидаемой доходности.
При наличии безрискового актива каждый
инвестор будет строить портфель
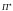 ,
обеспечивающий эффективную границу
множества инвестиционных возможностей
комбинаций безрискового актива и
портфелей рисковых активов.
,
обеспечивающий эффективную границу
множества инвестиционных возможностей
комбинаций безрискового актива и
портфелей рисковых активов.



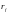
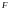

42. Задача максимизации ожидаемой доходности портфеля: математич постановка и графич иллюстрация.(графич иллюстрации нету)
Задача
записывается след образом:
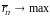 ,
,
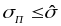 ,
,
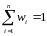 ,
,
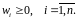 .
.
В
этой оптимизационной задаче в качестве
переменных выступают доли
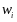 ,
,
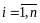 ,
финансовых активов в портфеле. В качестве
целевой функции выступает ожидаемая
доходность портфеля, зависящая от долей
,
финансовых активов в портфеле. В качестве
целевой функции выступает ожидаемая
доходность портфеля, зависящая от долей
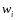 ,
,
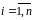 ,
(эта зависимость описывается формулой:
,
(эта зависимость описывается формулой:
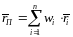 ).
Левая часть ограничения
–
это стандартное отклонение доходности
портфеля, также зависящее от долей
).
Левая часть ограничения
–
это стандартное отклонение доходности
портфеля, также зависящее от долей
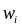 ,
,
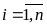 ,
(эта зависимость описывается формулой:
,
(эта зависимость описывается формулой:
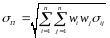 ).
Правая часть ограничения
).
Правая часть ограничения
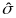 – это заданный max
допустимый уровень риска.
– это заданный max
допустимый уровень риска.
Геометрически решение задачи максимизации ожидаемой доходности