
- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
36. Использование линейной модели вероятности для оценки кредитного риска
Линейная модель вероятности для оценки кредитного риска имеет вид:
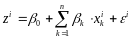 , ,
, ,
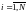 (1) Где k
- вид показателя, i
– номер наблюдения,
(1) Где k
- вид показателя, i
– номер наблюдения,
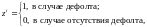
-
значение k-го
финансового показателя для i-го
наблюдения, ,
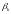 ,
,
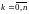 , – коэффициенты регрессии, – случайное
отклонение.
, – коэффициенты регрессии, – случайное
отклонение.
Показатели
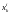 находятся с помощью финансовой отчетности
заемщика, например:
находятся с помощью финансовой отчетности
заемщика, например:
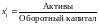 ,
,
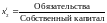 .
.
В модели предполагается, что для потенциального заемщика имеет место равенство, аналогичное равенствам (1), т.е.
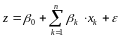 , (2)
, (2)
где
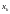 -
(известное) значение k-го
показателя потенциального заемщика.
-
(известное) значение k-го
показателя потенциального заемщика.
Заметим, что
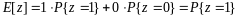 . (3)
. (3)
С другой стороны, как следует из равенства (2):
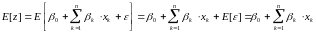 . (4)
. (4)
Из равенств (3) и (4) вытекает, что
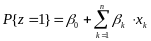 . (5)
. (5)
С
помощью значений
и
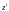 методом наименьших квадратов определяются
оценки
методом наименьших квадратов определяются
оценки
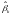 коэффициентов
(т.е. решается задача:
коэффициентов
(т.е. решается задача:
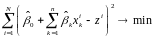 ).
).
Для потенциального заемщика строится прогнозное значение вероятности дефолта по формуле:
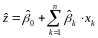 , (6)
, (6)
Основным
недостатком данной модели является то,
что прогнозное значение
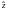 вероятности дефолта может не принадлежать
отрезку
вероятности дефолта может не принадлежать
отрезку
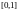 .
Модели логит и пробит (которые мы
рассмотрим ниже) позволяют избежать
эту проблему.
.
Модели логит и пробит (которые мы
рассмотрим ниже) позволяют избежать
эту проблему.
(Как
будет показано в следующем параграфе,
в моделях логит и пробит
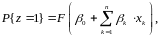 где
где
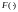 – функция, область значений которой –
нтервал , и для потенциального заемщика
прогнозное значение вероятности дефолта
полагается равным
– функция, область значений которой –
нтервал , и для потенциального заемщика
прогнозное значение вероятности дефолта
полагается равным
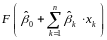 .)
.)
37 Использование моделей логит и пробит для оценки кредитного риска
В
моделях логит и пробит предполагается,
что для некоторого (ненаблюдаемого)
показателя дефолта
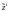 выполнены равенства
выполнены равенства
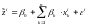 ,
, (7)
для известных наблюдений, и равенство
,
, (7)
для известных наблюдений, и равенство
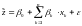 (8)
(8)
для
потенциального заемщика. Причем без
ограничения общности можно считать,
что стандартные отклонения случайных
ошибок
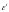 и
и
 равны 1. Обозначим через
равны 1. Обозначим через
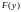 функцию распределения случайных ошибок
и
.
В модели логит в качестве
функцию распределения случайных ошибок
и
.
В модели логит в качестве
![]() выступает функция логистического
распределения:
выступает функция логистического
распределения:
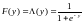 , (9)
а в модели пробит – функция стандартного
нормального распределения:
, (9)
а в модели пробит – функция стандартного
нормального распределения:
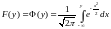 .(10)
.(10)
В
моделях логит и пробит, считается, что
(наблюдаемые) показатели дефолта
и
 связаны с (ненаблюдаемыми) показателями
и
связаны с (ненаблюдаемыми) показателями
и
 следующим образом:
следующим образом:
(11)
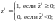
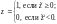 (12)
(12)
Из (8) и (12) следует, что
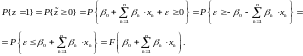 (13)
(13)
Таким
образом,
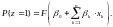 (14)
Заметим, что из (14) следует, что
(14)
Заметим, что из (14) следует, что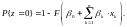 (15)
(15)
Отметим, что для (известных) наблюдений имеют место равенства, аналогичные (14) и (15), т.е.
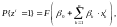
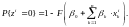 (16)
(16)
(17)
Оценки коэффициентов определяются методом максимального правдоподобия.
В силу равенств (16) и (17) функция правдоподобия для моделей логит и пробит имеет вид:
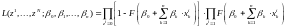 .
(18)
.
(18)
Легко показать, что формулу (18) можно записать в следующем виде:
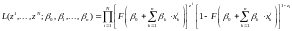 .
(19)
.
(19)
Оценки
получаются в результате максимизации
функции максимального правдоподобия
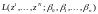 по параметрам
по параметрам
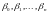 .Отметим,
что максимизация функции правдоподобия
эквивалентна максимизации логарифмической
функции правдоподобия. (Напомним, что
логарифмическая функция правдоподобия
равна натуральному логарифму функции
правдоподобия.) Найдем логарифмическую
функцию правдоподобия для моделей логит
и пробит.Прологарифмировав формулу
(19), получим:
.Отметим,
что максимизация функции правдоподобия
эквивалентна максимизации логарифмической
функции правдоподобия. (Напомним, что
логарифмическая функция правдоподобия
равна натуральному логарифму функции
правдоподобия.) Найдем логарифмическую
функцию правдоподобия для моделей логит
и пробит.Прологарифмировав формулу
(19), получим:
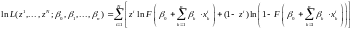 .
(20)
.
(20)
