
- •Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Непрерывная капитализация процента: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.
- •Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.
- •Текущая и будущая стоимости последовательности платежей: экономический смысл и нахождение.
- •Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.
- •Продолжительность последовательности платежей и ее использование для оценки чувствительности текущей стоимости последовательности платежей к изменению процентной ставки.
- •Конечная рента: вывод формул для текущей и будущей стоимости, продолжительность.
- •Вечная рента: вывод формул для текущей стоимости и продолжительности.
- •Свободные денежные потоки и горизонт оценивания свободных денежных потоков инвестиционного проекта.
- •Текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Чистая текущая стоимость инвестиционного проекта: формула и экономический смысл.
- •Внутренняя доходность инвестиционного проекта: уравнение и экономический смысл.
- •17 Модель с постоянным процентным ростом свободных денежных потоков
- •18 Задача оптимального финансирования проекта
- •19 Задача оптимального выбора инвестиционных проектов
- •20 Анализ чувствительности денежных потоков проекта
- •Анализ безубыточности инвестиционного проекта.
- •Уровень инфляции, номинальная и реальная процентные ставки, и их взаимосвязь (вывод формулы).
- •Учет инфляции при моделировании денежных потоков инвестиционного проекта.
- •Математическое моделирование финансового риска; доказать, что стандартное отклонение является мерой финансового риска (для случая нормального распределения денежного потока).
- •Имитационное моделирование денежных потоков инвестиционного проекта.
- •26. Облигации: платежи, текущая стоимость (вывод формулы и экономический смысл)
- •27. Доходность к погашению облигации: уравнение и экономический смысл.
- •28. Чистые доходности облигаций, их экономический смысл и методы нахождения.
- •29 Синтетические бескупонные облигации: экономический смысл и нахождение.
- •31.Форвардные доходности облигаций: нахождение и экономический смысл.
- •32.Продолжительность портфеля облигаций (вывод формулы).
- •33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
- •34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
- •36. Использование линейной модели вероятности для оценки кредитного риска
- •37 Использование моделей логит и пробит для оценки кредитного риска
- •38 Модели, основанные на регрессии.
- •39 Использование множественного дискриминантногго анализа для оценки кредитного риска.
- •41. Множество инвест возможностей портфелей, понятие эффективного портфеля, эффективная граница множества инвест возможностей: эк смысл и графическая иллюстрация.
- •43. Задача минимизации риска портфеля: математическая постановка и графическая иллюстрация.
- •44. Задача максимизации полезности инвестора: математическая постановка и графическая иллюстрация.
- •45. Комбинации портфеля и безрискового актива: ожидаемая доходность, стандартное отклонение, множество инвест возможностей, коэффициент "тета".
- •46 Оптимизация портфеля при наличии безрискового актива
32.Продолжительность портфеля облигаций (вывод формулы).
Поскольку
портфель облигаций выплачивает
последовательность платежей,
продолжительность портфеля облигаций
находится по формуле (12) главы 2, т.е.
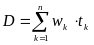 ,(1)
где wk
– доля текущей стоимости k-го
платежа портфеля в текущей стоимости
портфеля,
– срок выплаты k-го
платежа портфеля, n
– количество платежей портфеля. Докажем,
что для продолжительности портфеля
облигаций справедлива формула:
,(1)
где wk
– доля текущей стоимости k-го
платежа портфеля в текущей стоимости
портфеля,
– срок выплаты k-го
платежа портфеля, n
– количество платежей портфеля. Докажем,
что для продолжительности портфеля
облигаций справедлива формула:
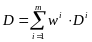 ,
(2) где wi
– доля
текущей стоимости облигаций i-го
вида в текущей стоимости портфеля,
,
(2) где wi
– доля
текущей стоимости облигаций i-го
вида в текущей стоимости портфеля,
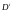 – продолжительность облигации i-го
вида, m
– количество видов облигаций в портфеле.
Введем следующие обозначения.
– продолжительность облигации i-го
вида, m
– количество видов облигаций в портфеле.
Введем следующие обозначения.
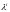 –
количество
облигаций i-го
вида в портфеле,
–
количество
облигаций i-го
вида в портфеле,
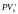 – текущая стоимость k-го
платежа облигации i-го
вида,
– текущая стоимость k-го
платежа облигации i-го
вида,
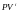 – текущая стоимость облигации i-го
вида,
– текущая стоимость облигации i-го
вида,
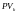 – текущая стоимость k-го
платежа портфеля,
– текущая стоимость k-го
платежа портфеля,
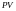 – текущая стоимость портфеля,
– текущая стоимость портфеля,
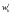 – доля текущей стоимости k-го
платежа облигации i-го
вида в текущей стоимости облигации i-го
вида.
– доля текущей стоимости k-го
платежа облигации i-го
вида в текущей стоимости облигации i-го
вида.
Очевидно, что имеют место следующие формулы:
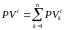 ,
, 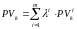 ,
,
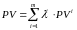 ,
,
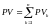 (3)
(3)
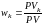 ,
,
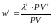 ,
, 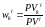 ,
, 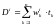 . (4)
. (4)
С учетом формул (3)-(4), имеем
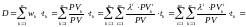
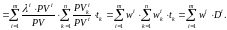
Таким образом, мы доказали формулу (2).
33.Чувствительность текущей стоимости портфеля облигаций к изменению доходностей облигации.
Предположим,
что ставка дисконтирования зависит
только от вида облигации. Тогда для
облигаций, входящих в портфель справедлива
формула (13) главы 2:
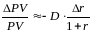 .
Таким образом,
.
Таким образом,
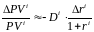 ,
,
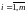 .
(7) Из (7) следует, что
.
(7) Из (7) следует, что
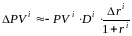 ,
.(8)
Легко заметить, что
,
.(8)
Легко заметить, что
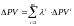 .
(9) Подставим (8) в (9):
.
(9) Подставим (8) в (9):
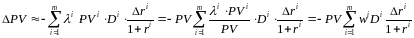 . (10)
. (10)
Предположим,
что
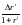 не зависит от вида облигации
.
Тогда из (10) следует, что
не зависит от вида облигации
.
Тогда из (10) следует, что
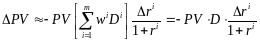 . (11)
. (11)
Разделив
(11) на
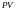 ,
получим:
,
получим:
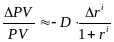 . (12)
Итак, в случае, когда
не зависит от вида облигации
,
для текущей стоимости портфеля облигаций
имеет место формула (12). Замечание. Если
в качестве ставок дисконтирования
. (12)
Итак, в случае, когда
не зависит от вида облигации
,
для текущей стоимости портфеля облигаций
имеет место формула (12). Замечание. Если
в качестве ставок дисконтирования
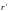 ,
,
выступают доходности самих облигаций,
то текущие стоимости облигаций
,
,
выступают доходности самих облигаций,
то текущие стоимости облигаций
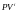 ,
,
равны ценам облигаций, а текущая стоимость
портфеля облигаций
равна рыночной стоимости портфеля
облигаций.
,
,
равны ценам облигаций, а текущая стоимость
портфеля облигаций
равна рыночной стоимости портфеля
облигаций.
34. Чувствительность собственного капитала финансовой организации к изменению доходностей облигаций.
Баланс
фирмы состоит из активов и пассивов.
Пассивы, в свою очередь, делятся на
обязательства и собственный капитал.
Обозначим активы, обязательства и
собственный капитал через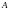 ,
,
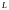 и
и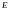 ,
соответственно.
,
соответственно.
Поскольку
активы равны пассивам, то
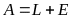 .
Отсюда имеем :
.
Отсюда имеем :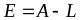 . (14)
. (14)
Существуют два основных метода оценки активов и обязательств:
метод, основанный на исторической стоимости (book value), т.е. стоимости, по которой активы и обязательства были приобретены;
метод, основанный на рыночной стоимости (market value), т.е. рыночной стоимости активов и обязательств в текущий момент времени.
Мы будем использовать второй метод. Таким образом, будем считать, что – рыночная стоимость активов, – рыночная стоимость обязательств, – рыночная стоимость собственного капитала.
Будем
считать, что активы и обязательства
финансовой организации состоят из
облигаций. (Под облигациями будем
понимать любые финансовые инструменты
с фиксированными платежами.) Таким
образом, активы и обязательства
представляют собой портфели облигаций.
Предположим, что
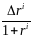 не зависит от вида облигаций, входящих
в активы и обязательства. Тогда как для
активов, так и для обязательств справедлива
формула (12). Следовательно,
не зависит от вида облигаций, входящих
в активы и обязательства. Тогда как для
активов, так и для обязательств справедлива
формула (12). Следовательно,
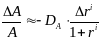 , (15)
, (15)
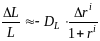 , (16)
, (16)
где
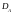 – продолжительность активов,
– продолжительность активов,
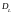 – продолжительность облигаций.
– продолжительность облигаций.
Из
формул (15), (16) следует, что
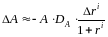 ,(17)
,(17)
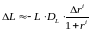 . (18)
. (18)
Из формулы (14)
следует, что
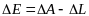 . (19)
. (19)
Подставим
(17) и (18) в (19):
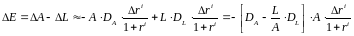 .(20)
.(20)
Обозначим
через
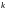 отношение обязательств к активам:
отношение обязательств к активам:
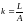 . (21)
Коэффициент
– это так называемый финансовый рычаг.
С учетом (21) формула (20) примет вид:
. (21)
Коэффициент
– это так называемый финансовый рычаг.
С учетом (21) формула (20) примет вид:
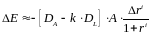 . (22)
Из формулы (22) следует, что финансовая
организация будет защищена от процентного
риска, если
. (22)
Из формулы (22) следует, что финансовая
организация будет защищена от процентного
риска, если
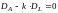 .
Поскольку этого чаще всего невозможно
достичь, для защиты от процентного риска
используют финансовые производные
(опционы и фьючерсы).
.
Поскольку этого чаще всего невозможно
достичь, для защиты от процентного риска
используют финансовые производные
(опционы и фьючерсы).
